A doksi online olvasásához kérlek jelentkezz be!
A doksi online olvasásához kérlek jelentkezz be!
| noszii | 2011. január 13. | |
|---|---|---|
| Köszönöm, remek doksi! | ||
Tartalmi kivonat
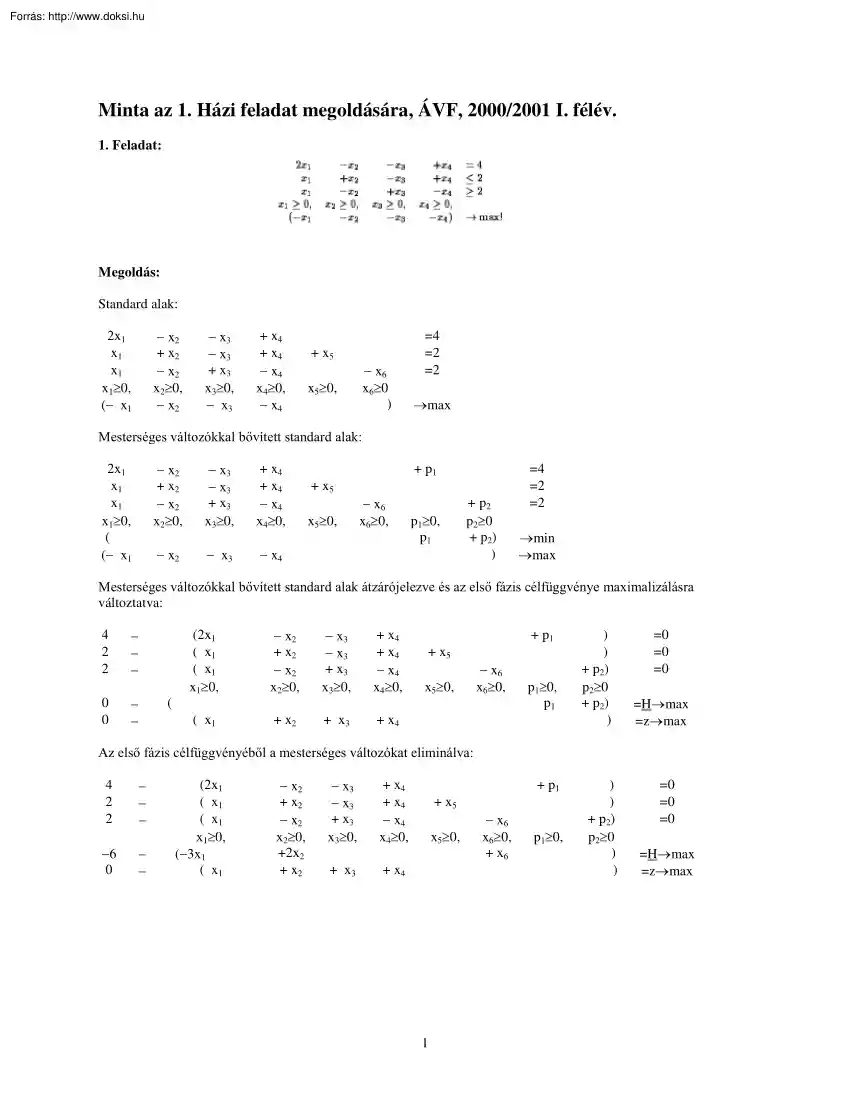
Minta az 1. Házi feladat megoldására, ÁVF, 2000/2001 I félév 1. Feladat: Megoldás: Standard alak: − x2 + x2 − x2 x2≥0, − x2 2x1 x1 x1 x1≥0, (− x1 − x3 − x3 + x3 x3≥0, − x3 + x4 + x4 − x4 x4≥0, − x4 + x5 − x6 x6≥0 ) x5≥0, =4 =2 =2 max Mesterséges változókkal bővített standard alak: 2x1 x1 x1 x1≥0, ( (− x1 − x2 + x2 − x2 x2≥0, − x3 − x3 + x3 x3≥0, + x4 + x4 − x4 x4≥0, − x2 − x3 − x4 + p1 + x5 x5≥0, − x6 x6≥0, p1≥0, p1 + p2 p2≥0 + p2) ) =4 =2 =2 min max Mesterséges változókkal bővített standard alak átzárójelezve és az első fázis célfüggvénye maximalizálásra változtatva: 4 2 2 0 0 − − − − − (2x1 ( x1 ( x1 x1≥0, − x2 + x2 − x2 x2≥0, − x3 − x3 + x3 x3≥0, + x4 + x4 − x4 x4≥0, ( x1 + x2 + x3 + x4 + p1 + x5 x5≥0, − x6 x6≥0, ( p1≥0, p1 ) ) + p2) p2≥0 + p2) ) =0 =0 =0 =Hmax =zmax Az első fázis célfüggvényéből a
mesterséges változókat eliminálva: 4 2 2 −6 0 − − − − − (2x1 ( x1 ( x1 x1≥0, (−3x1 ( x1 − x2 + x2 − x2 x2≥0, +2x2 + x2 − x3 − x3 + x3 x3≥0, + x4 + x4 − x4 x4≥0, + x3 + x4 + p1 + x5 x5≥0, 1 − x6 x6≥0, + x6 p1≥0, ) ) + p2) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 x5 p2 ∆Hj ∆zj xB 4 2 2 −6 0 x1 2 1 1 −3 1 ↑ x2 −1 1 −1 2 1 x3 −1 −1 1 0 1 x4 1 1 −1 0 1 x5 0 1 0 0 0 x6 0 0 −1 1 0 p2 0 0 1 0 0 θi 2 2 2 p2 −2 −1 1 3 −1 θi 0 0 − p1 1 0 0 0 0 ← Az I. fázis iterációi: B1 p1 x5 x1 ∆Hj ∆zj xB 0 0 2 0 −2 x1 0 0 1 0 0 x2 1 2 −1 −1 2 ↑ x3 −3 −2 1 3 0 x4 3 2 −1 −3 2 x5 0 1 0 0 0 x6 2 1 −1 −2 1 p1 1 0 0 0 0 B2 x2 x5 x1 ∆Hj ∆zj xB 0 0 2 0 −2 x1 0 0 1 0 0 x2 1 0 0 0 0 x3 −3 4 −2 0 6 x4 3 −4 2 0 −4 x5 0 1 0 0 0 x6 2 −3 1 0 −3 p1 1 −2 1 1 −2 x3 −3 4 −2 6 x4 3 −4 2 −4 x5 0 1 0 0 x6 2 −3 1 −3 ↑
θi 0 − 2 x3 − 3/2 − 1/2 − 1/2 3/2 x4 3/2 1/2 1/2 1/2 x5 0 1 0 0 x6 1 0 0 0 p2 −2 3 −1 1 3 ← θi A II. fázis iterációi: B2 x2 x5 x1 ∆zj xB 0 0 2 −2 x1 0 0 1 0 x2 1 0 0 0 B3 x6 x5 x1 ∆zj xB 0 0 2 −2 x1 0 0 1 0 x2 1/2 3/2 − 1/2 3/2 ← A feladatnak létezik megengedett megoldása és véges optimuma! Az optimális megoldás: x1 = 2.0, x2 = 00, x3 = 00, x4 = 00, zopt = − 20 2 2. Feladat: Megoldás: Standard alak: x1 2x1 −2x1 x1≥0, (−2x1 +2 x2 −2 x2 − x2 x2≥0, −2 x2 + x3 −2x3 −2 x3 x3≥0, + x3 − x4 − x4 +2 x4 x4≥0, + x4 − x5 =2 =4 =3 + x6 x5≥0, x6≥0, − x7 x7≥0 ) max Mesterséges változókkal bővített standard alak: x1 2x1 −2x1 x1≥0, ( (−2x1 +2 x2 −2 x2 − x2 x2≥0, + x3 −2x3 −2 x3 x3≥0, − x4 − x4 +2 x4 x4≥0, −2 x2 + x3 + x4 − x5 +p1 + x6 x5≥0, x6≥0, − x7 x7≥0, p1≥0, p1 +p2 p2≥0 +p2) ) =2 =4 =3 min max Mesterséges változókkal bővített
standard alak átzárójelezve és az első fázis célfüggvénye maximalizálásra változtatva: 2 4 3 0 0 − − − − − (x1 (2x1 (−2x1 x1≥0, ( (2x1 2 x2 −2 x2 − x2 x2≥0, +2 x2 + x3 −2 x3 −2 x3 x3≥0, − x3 − x4 − x4 +2 x4 x4≥0, − x5 + p1 + x6 x5≥0, x6≥0, − x7 x7≥0, p1≥0, p1 − x4 ) ) + p2) p2≥0 + p2) ) =0 =0 =0 =Hmax =zmax Az első fázis célfüggvényéből a mesterséges változókat eliminálva: 2 4 3 0 0 − − − − − (x1 (2x1 (−2x1 x1≥0, (x1 (2x1 2 x2 −2 x2 − x2 x2≥0, − x2 +2 x2 + x3 −2 x3 −2 x3 x3≥0, + x3 − x3 − x4 − x4 +2 x4 x4≥0, − x4 − x4 − x5 + p1 + x6 x5≥0, + x5 3 x6≥0, − x7 x7≥0, + x7 p1≥0, ) ) + p2) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 x6 p2 ∆Hj ∆zj xB 2 4 3 −5 0 x1 1 2 −2 1 2 x2 2 −2 −1 −1 2 ↑ x3 1 −2 −2 1 −1 x4 −1 −1 2 −1 −1 x5 −1 0 0 1 0 x6 0 1 0 0 0 x7 0 0 −1 1 0 p1 1 0 0
0 0 p2 0 0 1 0 0 θi 2 − − x6 0 1 0 0 0 p1 1/2 1 1/2 1/2 −1 p2 0 0 1 0 0 θi − − 8/3 ← Az I. fázis iterációi: B1 x2 x6 p2 ∆Hj ∆zj xB 1 6 4 −4 −2 x1 1/2 3 3/2 3/2 1 x2 1 0 0 0 0 x3 1/2 −1 −3/2 3/2 −2 x4 − 1/2 −2 3/2 − 3/2 0 ↑ x5 − 1/2 −1 − 1/2 1/2 1 B2 x2 x6 p2 ∆Hj ∆zj xB 7/3 34/3 8/3 0 −2 x1 1 5 1 0 1 x2 1 0 0 0 0 x3 0 −3 −1 0 −2 x4 0 0 1 0 0 x5 − 2/3 − 5/3 − 1/3 0 1 x6 0 1 0 0 0 p1 2/3 5/3 1/3 1 −1 x2 1 0 0 0 x3 0 −3 −1 −2 ↑ x4 0 0 1 0 x5 − 2/3 − 5/3 − 1/3 1 x6 0 1 0 0 θi p2 1/3 4/3 2/3 1 0 ← θi A II. fázis iterációi: B2 x2 x6 p2 ∆zj xB 7/3 34/3 8/3 −2 x1 1 5 1 1 A feladat célfüggvénye az adott korlátozó feltételek mellett tetszőlegesen nagy értéket felvehet, vagyis a feladatnak nincs véges optimuma. 4 3. Feladat: Megoldás: Standard alak: 2 x1 − 2x1 2 x1 x1≥0, (2 x1 + x2 − 2 x2 + x2 x2≥0, − x2 + x3 +2 x3 + 2 x3 x3≥0, −2 x3 −2
x4 + x4 − 2 x4 x4≥0, − x4 − x5 x5≥0, +x6 x6≥0 ) =4 =2 =4 max Mesterséges változókkal bővített standard alak: 2 x1 − 2x1 2 x1 x1≥0, ( (2 x1 + x2 − 2 x2 + x2 x2≥0, + x3 +2 x3 + 2 x3 x3≥0, −2 x4 + x4 − 2 x4 x4≥0, − x2 −2 x3 − x4 − x5 x5≥0, +p1 +p2 =4 =2 =4 + p2) ) min max +x6 x6≥0 p1 Mesterséges változókkal bővített standard alak átzárójelezve és az első fázis célfüggvénye maximalizálásra változtatva: 4 2 4 − − − 0 0 − − (2x1 (−2 x1 ( 2 x1 x1≥0, ( (−2x1 + x2 − 2 x2 + x2 x2≥0, + x3 +2 x3 +2 x3 x3≥0, − 2x4 + x4 −2 x4 x4≥0, + x2 +2 x3 + x4 − x5 x5≥0, + p1 + x6 x6≥0, p1≥0, p1 ) + p2) ) p2≥0 + p2) ) =0 =0 =0 =Hmax =zmax Az első fázis célfüggvényéből a mesterséges változókat eliminálva: 4 2 4 − − − −6 0 − − (2x1 (−2 x1 ( 2 x1 x1≥0, ( (−2x1 + x2 − 2 x2 + x2 x2≥0, + x2 + x2 + x3 +2 x3 +2 x3 x3≥0, −3 x3 +2 x3 − 2x4 + x4
−2 x4 x4≥0, + x4 + x4 − x5 x5≥0, + x5 5 + p1 + x6 x6≥0, p1≥0, ) + p2) ) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 p2 x6 ∆Hj ∆zj xB 4 2 4 −6 0 x1 2 −2 2 0 −2 x2 1 −2 1 1 1 x3 1 2 2 −3 2 ↑ x4 −2 1 −2 1 1 x5 −1 0 0 1 0 p2 0 1 0 0 0 θi 4 1 2 p1 1 0 0 0 0 p2 −1/2 1/2 −1 3/2 −1 θi 3/2 − 2/3 x6 −2/3 1/3 1/3 2/3 −1 p1 1 0 0 0 0 x6 0 0 1 0 0 p1 1 0 0 0 0 ← Az I. fázis iterációi: B1 p1 x3 x6 ∆Hj ∆zj xB 3 1 2 −3 −2 x1 3 −1 4 −3 0 x2 2 −1 3 −2 3 ↑ x3 0 1 0 0 0 x4 −5/2 1/2 −3 5/2 0 B2 p1 x3 x2 ∆Hj ∆zj xB 5/3 5/3 2/3 −5/3 −4 x1 1/3 1/3 4/3 −1/3 −4 ↑ x2 0 0 1 0 0 x3 0 1 0 0 0 B3 p1 x3 x1 ∆Hj ∆zj xB 3/2 3/2 1/2 −3/2 −2 x1 0 0 1 0 0 x2 −1/4 −1/4 3/4 1/4 3 x3 0 1 0 0 0 x5 −1 0 0 1 0 x4 −1/2 −1/2 −1 1/2 3 x4 −1/4 −1/4 − 3/4 1/4 0 x6 0 0 1 0 0 x5 −1 0 0 1 0 x5 −1 0 0 1 0 x6 −3/4 1/4 1/4 3/4 0 p2 1/6 1/6 −1/3 7/6
0 p1 1 0 0 0 0 ← θi 5 5 1/2 p2 1/4 1/4 −1/4 13/12 −1 ← θi A feladatnak nincs megengedett megoldása, mert a bevezetett mesterséges változók összegének a minimuma 3/2 és ez nagyobb mint nulla. Budapest, 2000. szeptember 27 Dr. Szántai Tamás sk főiskolai tanár 6
mesterséges változókat eliminálva: 4 2 2 −6 0 − − − − − (2x1 ( x1 ( x1 x1≥0, (−3x1 ( x1 − x2 + x2 − x2 x2≥0, +2x2 + x2 − x3 − x3 + x3 x3≥0, + x4 + x4 − x4 x4≥0, + x3 + x4 + p1 + x5 x5≥0, 1 − x6 x6≥0, + x6 p1≥0, ) ) + p2) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 x5 p2 ∆Hj ∆zj xB 4 2 2 −6 0 x1 2 1 1 −3 1 ↑ x2 −1 1 −1 2 1 x3 −1 −1 1 0 1 x4 1 1 −1 0 1 x5 0 1 0 0 0 x6 0 0 −1 1 0 p2 0 0 1 0 0 θi 2 2 2 p2 −2 −1 1 3 −1 θi 0 0 − p1 1 0 0 0 0 ← Az I. fázis iterációi: B1 p1 x5 x1 ∆Hj ∆zj xB 0 0 2 0 −2 x1 0 0 1 0 0 x2 1 2 −1 −1 2 ↑ x3 −3 −2 1 3 0 x4 3 2 −1 −3 2 x5 0 1 0 0 0 x6 2 1 −1 −2 1 p1 1 0 0 0 0 B2 x2 x5 x1 ∆Hj ∆zj xB 0 0 2 0 −2 x1 0 0 1 0 0 x2 1 0 0 0 0 x3 −3 4 −2 0 6 x4 3 −4 2 0 −4 x5 0 1 0 0 0 x6 2 −3 1 0 −3 p1 1 −2 1 1 −2 x3 −3 4 −2 6 x4 3 −4 2 −4 x5 0 1 0 0 x6 2 −3 1 −3 ↑
θi 0 − 2 x3 − 3/2 − 1/2 − 1/2 3/2 x4 3/2 1/2 1/2 1/2 x5 0 1 0 0 x6 1 0 0 0 p2 −2 3 −1 1 3 ← θi A II. fázis iterációi: B2 x2 x5 x1 ∆zj xB 0 0 2 −2 x1 0 0 1 0 x2 1 0 0 0 B3 x6 x5 x1 ∆zj xB 0 0 2 −2 x1 0 0 1 0 x2 1/2 3/2 − 1/2 3/2 ← A feladatnak létezik megengedett megoldása és véges optimuma! Az optimális megoldás: x1 = 2.0, x2 = 00, x3 = 00, x4 = 00, zopt = − 20 2 2. Feladat: Megoldás: Standard alak: x1 2x1 −2x1 x1≥0, (−2x1 +2 x2 −2 x2 − x2 x2≥0, −2 x2 + x3 −2x3 −2 x3 x3≥0, + x3 − x4 − x4 +2 x4 x4≥0, + x4 − x5 =2 =4 =3 + x6 x5≥0, x6≥0, − x7 x7≥0 ) max Mesterséges változókkal bővített standard alak: x1 2x1 −2x1 x1≥0, ( (−2x1 +2 x2 −2 x2 − x2 x2≥0, + x3 −2x3 −2 x3 x3≥0, − x4 − x4 +2 x4 x4≥0, −2 x2 + x3 + x4 − x5 +p1 + x6 x5≥0, x6≥0, − x7 x7≥0, p1≥0, p1 +p2 p2≥0 +p2) ) =2 =4 =3 min max Mesterséges változókkal bővített
standard alak átzárójelezve és az első fázis célfüggvénye maximalizálásra változtatva: 2 4 3 0 0 − − − − − (x1 (2x1 (−2x1 x1≥0, ( (2x1 2 x2 −2 x2 − x2 x2≥0, +2 x2 + x3 −2 x3 −2 x3 x3≥0, − x3 − x4 − x4 +2 x4 x4≥0, − x5 + p1 + x6 x5≥0, x6≥0, − x7 x7≥0, p1≥0, p1 − x4 ) ) + p2) p2≥0 + p2) ) =0 =0 =0 =Hmax =zmax Az első fázis célfüggvényéből a mesterséges változókat eliminálva: 2 4 3 0 0 − − − − − (x1 (2x1 (−2x1 x1≥0, (x1 (2x1 2 x2 −2 x2 − x2 x2≥0, − x2 +2 x2 + x3 −2 x3 −2 x3 x3≥0, + x3 − x3 − x4 − x4 +2 x4 x4≥0, − x4 − x4 − x5 + p1 + x6 x5≥0, + x5 3 x6≥0, − x7 x7≥0, + x7 p1≥0, ) ) + p2) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 x6 p2 ∆Hj ∆zj xB 2 4 3 −5 0 x1 1 2 −2 1 2 x2 2 −2 −1 −1 2 ↑ x3 1 −2 −2 1 −1 x4 −1 −1 2 −1 −1 x5 −1 0 0 1 0 x6 0 1 0 0 0 x7 0 0 −1 1 0 p1 1 0 0
0 0 p2 0 0 1 0 0 θi 2 − − x6 0 1 0 0 0 p1 1/2 1 1/2 1/2 −1 p2 0 0 1 0 0 θi − − 8/3 ← Az I. fázis iterációi: B1 x2 x6 p2 ∆Hj ∆zj xB 1 6 4 −4 −2 x1 1/2 3 3/2 3/2 1 x2 1 0 0 0 0 x3 1/2 −1 −3/2 3/2 −2 x4 − 1/2 −2 3/2 − 3/2 0 ↑ x5 − 1/2 −1 − 1/2 1/2 1 B2 x2 x6 p2 ∆Hj ∆zj xB 7/3 34/3 8/3 0 −2 x1 1 5 1 0 1 x2 1 0 0 0 0 x3 0 −3 −1 0 −2 x4 0 0 1 0 0 x5 − 2/3 − 5/3 − 1/3 0 1 x6 0 1 0 0 0 p1 2/3 5/3 1/3 1 −1 x2 1 0 0 0 x3 0 −3 −1 −2 ↑ x4 0 0 1 0 x5 − 2/3 − 5/3 − 1/3 1 x6 0 1 0 0 θi p2 1/3 4/3 2/3 1 0 ← θi A II. fázis iterációi: B2 x2 x6 p2 ∆zj xB 7/3 34/3 8/3 −2 x1 1 5 1 1 A feladat célfüggvénye az adott korlátozó feltételek mellett tetszőlegesen nagy értéket felvehet, vagyis a feladatnak nincs véges optimuma. 4 3. Feladat: Megoldás: Standard alak: 2 x1 − 2x1 2 x1 x1≥0, (2 x1 + x2 − 2 x2 + x2 x2≥0, − x2 + x3 +2 x3 + 2 x3 x3≥0, −2 x3 −2
x4 + x4 − 2 x4 x4≥0, − x4 − x5 x5≥0, +x6 x6≥0 ) =4 =2 =4 max Mesterséges változókkal bővített standard alak: 2 x1 − 2x1 2 x1 x1≥0, ( (2 x1 + x2 − 2 x2 + x2 x2≥0, + x3 +2 x3 + 2 x3 x3≥0, −2 x4 + x4 − 2 x4 x4≥0, − x2 −2 x3 − x4 − x5 x5≥0, +p1 +p2 =4 =2 =4 + p2) ) min max +x6 x6≥0 p1 Mesterséges változókkal bővített standard alak átzárójelezve és az első fázis célfüggvénye maximalizálásra változtatva: 4 2 4 − − − 0 0 − − (2x1 (−2 x1 ( 2 x1 x1≥0, ( (−2x1 + x2 − 2 x2 + x2 x2≥0, + x3 +2 x3 +2 x3 x3≥0, − 2x4 + x4 −2 x4 x4≥0, + x2 +2 x3 + x4 − x5 x5≥0, + p1 + x6 x6≥0, p1≥0, p1 ) + p2) ) p2≥0 + p2) ) =0 =0 =0 =Hmax =zmax Az első fázis célfüggvényéből a mesterséges változókat eliminálva: 4 2 4 − − − −6 0 − − (2x1 (−2 x1 ( 2 x1 x1≥0, ( (−2x1 + x2 − 2 x2 + x2 x2≥0, + x2 + x2 + x3 +2 x3 +2 x3 x3≥0, −3 x3 +2 x3 − 2x4 + x4
−2 x4 x4≥0, + x4 + x4 − x5 x5≥0, + x5 5 + p1 + x6 x6≥0, p1≥0, ) + p2) ) p2≥0 ) ) =0 =0 =0 =Hmax =zmax Az induló szimplex tábla: B0 p1 p2 x6 ∆Hj ∆zj xB 4 2 4 −6 0 x1 2 −2 2 0 −2 x2 1 −2 1 1 1 x3 1 2 2 −3 2 ↑ x4 −2 1 −2 1 1 x5 −1 0 0 1 0 p2 0 1 0 0 0 θi 4 1 2 p1 1 0 0 0 0 p2 −1/2 1/2 −1 3/2 −1 θi 3/2 − 2/3 x6 −2/3 1/3 1/3 2/3 −1 p1 1 0 0 0 0 x6 0 0 1 0 0 p1 1 0 0 0 0 ← Az I. fázis iterációi: B1 p1 x3 x6 ∆Hj ∆zj xB 3 1 2 −3 −2 x1 3 −1 4 −3 0 x2 2 −1 3 −2 3 ↑ x3 0 1 0 0 0 x4 −5/2 1/2 −3 5/2 0 B2 p1 x3 x2 ∆Hj ∆zj xB 5/3 5/3 2/3 −5/3 −4 x1 1/3 1/3 4/3 −1/3 −4 ↑ x2 0 0 1 0 0 x3 0 1 0 0 0 B3 p1 x3 x1 ∆Hj ∆zj xB 3/2 3/2 1/2 −3/2 −2 x1 0 0 1 0 0 x2 −1/4 −1/4 3/4 1/4 3 x3 0 1 0 0 0 x5 −1 0 0 1 0 x4 −1/2 −1/2 −1 1/2 3 x4 −1/4 −1/4 − 3/4 1/4 0 x6 0 0 1 0 0 x5 −1 0 0 1 0 x5 −1 0 0 1 0 x6 −3/4 1/4 1/4 3/4 0 p2 1/6 1/6 −1/3 7/6
0 p1 1 0 0 0 0 ← θi 5 5 1/2 p2 1/4 1/4 −1/4 13/12 −1 ← θi A feladatnak nincs megengedett megoldása, mert a bevezetett mesterséges változók összegének a minimuma 3/2 és ez nagyobb mint nulla. Budapest, 2000. szeptember 27 Dr. Szántai Tamás sk főiskolai tanár 6




 Ahogy közeledik a történelem érettségi, sokan döbbennek rá, hogy nem készültek fel eléggé az esszéírás feladatra. Módszertani útmutatónkban kitérünk a történet térbeli és időbeli elhelyezésére, a források elemzésére és az eseményeket alakító tényezőkre is.
Ahogy közeledik a történelem érettségi, sokan döbbennek rá, hogy nem készültek fel eléggé az esszéírás feladatra. Módszertani útmutatónkban kitérünk a történet térbeli és időbeli elhelyezésére, a források elemzésére és az eseményeket alakító tényezőkre is.