Gazdasági Ismeretek | Pénzügy » Pénzügyi számítások

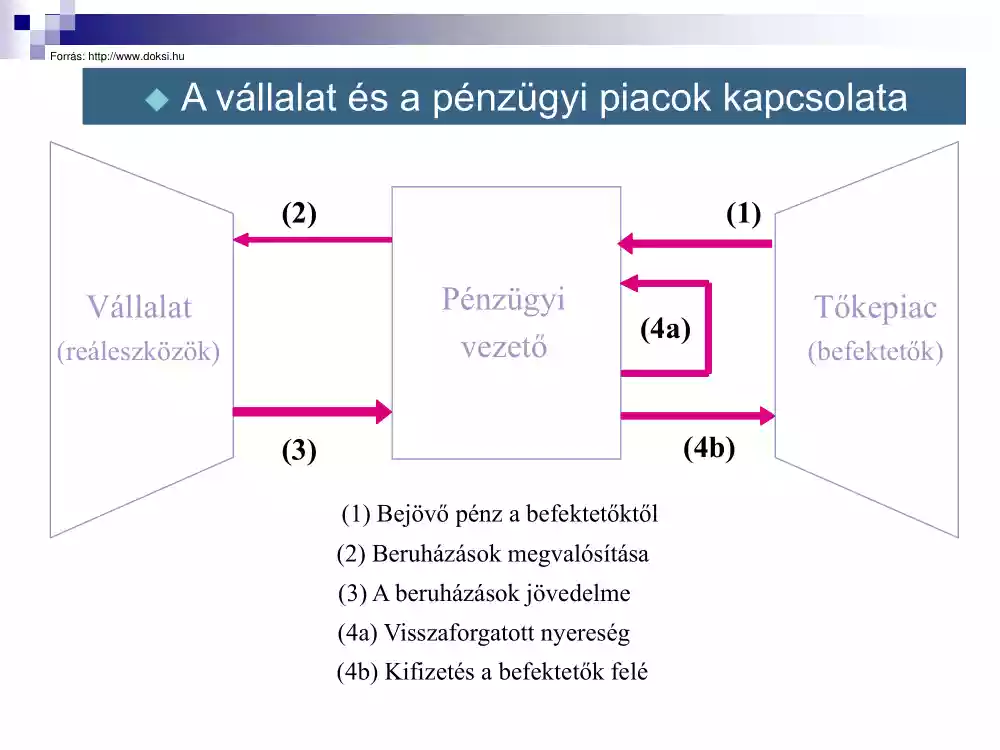
 A vállalat és a pénzügyi piacok kapcsolata (2) (1) Pénzügyi vezető Vállalat (reáleszközök) (4a) (4b) (3) (1) Bejövő pénz a befektetőktől (2) Beruházások megvalósítása (3) A beruházások jövedelme (4a) Visszaforgatott nyereség (4b) Kifizetés a befektetők felé Tőkepiac (befektetők)  Kamatszámítás •Kamatszámítási módszerek •Folytonos kamatozás •Effektív kamatláb meghatározása •Nominális és reálhozam  Kamatszámítás  Egyszerű kamatozás: FVt = C0 ⋅ (1 + r ⋅ n)  Kamatos kamatozás: FVn = C0 ⋅ (1 + r ) n  Folytonos kamatozás: FVn = C0 ⋅ e r ⋅n Reál effektív kamatláb: i m reff = (1 + ) − 1 m   Példa1:Egyszerű és kamatos kamatozás Egyszerű kamatozás Kamatos kamatozás Év Év eleji egyenleg Kamat ZáróÉv eleji egyenleg egyenleg Kamat Záróegyenleg 1 100 10 ? 100 10 ? 2 ? 10 ? ? ? ? 3 ? 10 ? ? ? ? 10 ? 10 ? ? ? ? 50 ? 10

? ? ? ? Egyszerű és kamatos kamatozás Egyszerű kamatozás Kamatos kamatozás Év Év eleji egyenleg Kamat ZáróÉv eleji egyenleg egyenleg Kamat Záróegyenleg 1 100 10 110 100 10 110 2 110 10 120 110 11 121 3 120 10 130 121 12.1 133.1 10 190 10 200 236 23.6 259.6 50 590 10 600 10 672 1 067 11 739 Kamatszámítás 20 18 16 14 12 10 8 6 4 2 0 10% Egyszerű Eltelt évek száma 30 27 24 21 18 15 12 9 6 10% Kamatos 3 0 Jövőérték   A tőkésítés hatása a jövőértékre Tőkésítések száma (m) Névleges kamatláb (i) Időegységre eső kamatláb (i/m) Jövőértéke Effektív kamatláb 1 6% ? ? ? 2 6% ? ? ? 4 6% ? ? ? 12 6% ? ? ? 52 6% ? ? ? 365 6% ? ? ?  A tőkésítés hatása a jövőértékre Tőkésítések száma (m) 1 2 4 12 Névleges kamatláb (i) 6% 6% 6% 6% Időegységre eső kamatláb (i/m) Jövőértéke Effektív kamatláb 6%

1.061 = 1.06 6% 3% 1.032 = 1.0609 6,09% 1,5% 1.0154 = 1.06136 6,136% 0,5% 1.00512 = 1.06168 6,168% 52 6% 0,1154% 365 6% 0,0164% 1.00115452 = 1.0618 1.000164365 = 1.06183 6,18% 6,183%  Reálkamatláb: 1 + nominális kamatláb 1 + reálkamatláb = 1 + inflációs ráta    Jelenérték számítás: A jelenérték jövőben esedékes pénzösszegek jelen időpontra vetített értéke. A jelenérték függ: 1. 2. 3. A tőke alternatív-költségétől A jövőben esedékes pénzösszegek nagyságától Időszakok számától   Jelenérték: Képlete:  Egy időszak esetén:  Több időszak esetén: Másképpen:  1  PV = FVn ⋅  n ( ) + 1 r   PV = C3 Cn C1 C2 + + + . + 1 + r (1 + r )2 (1 + r )3 (1 + r )n n Ct PV = ∑ t ( ) 1 + r t =1   Egy befektetés induló tőkeszükséglete 5 millió Ft. Becslések szerint a befektetésből négy éven keresztül a következő jövedelmek várhatók

időrendben:      Jelenérték-számítás példa 1: 1. év végén: 1 500 000 Ft 2. év végén: 1 800 000 Ft 3. év végén: 2 400 000 Ft 4. év végén: 2 800 000 Ft Érdemes e megvalósítani a beruházást, ha a tőke alternatív költsége 15%?  Jelenérték-számítás példa 1: 1500000 1800000 2400000 2800000 PV = + + + = 5844354,473 2 3 4 1,15 (1,15) (1,15) (1,15) NPV = −5000000 + 5844354,473 = 844354,473   Jelenérték-számítás példa 2: Egy olajkitermelő társaság új olajlelőhely feltárását fontolgatja. A törvények szerint a lelőhelyet legalább 3 évig kell üzemeltetni. A várható kitermelési adatokat a következő táblázatban összegezték:  Jelenérték-számítás példa 2: Év 1. 2. 3. Termelés (hordó) 50000 60000 45000 4. 35000      Jelenérték-számítás példa 2: Számításaik szerint az olaj ára a következő 4 évben stabilan 20$/hordó lesz. A lelőhely

kiaknázása C0= 2 millió $ értékű tőkeberuházást tesz szükségessé. A folyó költségek az alábbiak: minden évben 200 munkást kell alkalmazni fejenként 2000$/év fizetéssel. A befektetett tőke évente 10 % -ot veszít értékéből az eredeti értékéhez képest. Az üzem bezárásakor (a 3. vagy a 4 év végén) a tőkejavakat számvitelben nyilvántartott értéken el tudják adni. Az üzem bezárásával kapcsolatban más költség vagy bevétel nem merül fel. A kezdőtőke előteremtéséhez saját forrást használnak fel és a piaci kamatláb évi 10%. A döntéshozók előtt felmerülő kérdés a következő: 3 vagy 4 évig üzemeltessék a lelőhelyet. Melyik alternatívát válassza a vállalat? 3 éves változat 1. év 2. év 3. év 4. év Bevétel 50000*20=1 m$ 1,2 m$ 0,9m$+ +1,4 m$= =2,3 m$ - Költség 200*2000+0,1 *2000000=0,6 m$ 0,6 m$ 0,6 m$ - 0,6 m$ 1,7 m$ - nyereség 1 m$-0,6 m$=0,4 m$ 400000 600000 1700000 PV = + + = 2136700$

1,1 1,21 1,331 NPV = −C0 + PV = −2000000 + 2136700 = 136700$ 1. év 2. év 3. év 4. év 1 m$ 1,2 m$ 0,9 m$ 0,7 m$+1,2 m$=1,9 m$ Költség 0,6 m$ 0,6 m$ 0,6 m$ 0,6 m$ Nyereség 0,4 m$ 0,6 m$ 0,3 m$ 1,3 m$ 4 éves Bevétel változat 400000 600000 300000 1300000 PV = + + + = 1972816,064$ 1,1 1,21 1,331 1,4641 NPV = −C0 + PV = −2000000 + 1972816,064 = −27183,39553$ Annuitás: Az annuitás egy meghatározott (véges) ideig tartó, egyenlő nagyságú pénzáramlás-sorozat.  Szokásos annuitás: pénzáramlások a periódusok végén jelentkeznek  Esedékes annuitás: pénzáramlások a periódusok elején várhatók  Annuitás  jövőértéke: Szokásos annuitás: FV = AN  Pl: 500000 Ft-ot kapunk 10 évig minden év végén. Mennyi a 10. év végén elérhető pénzösszeg, ha a piaci kamatláb r=10%? 1,110 − 1 FV = 500000 ⋅ = 7968712,3 Ft 0,1 n ( 1+ r) ⋅ r −1 Annuitás  jövőértéke: Esedékes

annuitás:  Pl. Mennyi az előző példában szereplő adatokkal elérhető pénzösszeg, ha esedékes annuitásról van szó?  (1 + r )n +1 − 1  FV = AN ⋅  − 1 r   1,111 − 1  − 1 = 8765583,531 Ft FV = 500000 ⋅  0,1   Annuitás  jelenértéke: Szokásos annuitás:  Pl.: 10 éven keresztül minden évben (év végén) 500000 Ft jövedelmet kapunk. Mennyit ér nekünk ez a pénzáramlás ma, ha a piaci kamatláb 10%? n ( 1+ r ) −1 PV = AN ⋅ n r ⋅ (1 + r ) r ⋅ (1 + r ) AN = PV ⋅ (1 + r )n − 1 10 ( 1,1) − 1 PV = 500000 ⋅ = 3072283,553 Ft 10 0,1⋅ (1,1) n Annuitás  jelenértéke: Esedékes annuitás:  Pl.: Mennyit ér ma az előző példában szereplő pénzáramlás, ha esedékes annuitásról van szó (vagyis mindig év elején fizet)?  (1 + r )n −1 − 1  PV = AN ⋅  + 1 n −1  r ⋅ (1 + r )  AN = PV ⋅ 1  (1 + r )n −1 − 1  + 1  n −1

 r ⋅ (1 + r )   (1,1)9 − 1  PV = 500000 ⋅  + 1 = 3379511,908 Ft 9  0,1⋅ (1,1)  Példa:  Lakáshitel: Egy Lakás megvásárlásához 15 millió Ft hitel felvételét tervezzük 10 évre (önerő nincs). A piacon elérhető legkedvezőbb THM évi 5%. A lakást megvásárlása után (mely egybeesik a hitelfelvétel időpontjával) azonnal bérbe adjuk. Mennyi legyen a havi bérleti díj, ha azt akarjuk, hogy az pont fedezze a hiteltörlesztés költségeit? Példa: Lakáshitel: 120 0,05  0,05  ⋅ 1 +  12  12  = 159098,2731 Ft AN = 15000000 ⋅ 120  0,05  1 +  −1 12   Örökjáradék  Periódusonként azonos nagyságú fix jövedelmet biztosít végtelen hosszú ideig C PV = r Példa örökjáradék:   500000 Az olimpiai bajnok PVolimpiaibajnok = = 100000000 Ft sportolók 30 éves 0,005 koruktól havi 500 ezer PVállam = 100 ⋅ PVolimpiaibajnok = 10mrd Ft forint juttatásban

részesülnek életük végéig. Mennyit ér neki 30 éves korában ez a pénzáramlás, ha az éves kamatláb 6%? Mennyibe kerül mindez az államnak ma, ha száz élő olimpiai bajnok van? Növekvő tagú örökjáradék:   Állandó ütemben növekszik a pénzösszeg Hogyan módosul az előző példa eredménye, ha g=0,001 C r−g 500000 PV = = 125000000 Ft 0,005 − 0,001 PV = Kötvény:    A kötvény fix kamatozású, általában hosszabb lejáratú hitelviszonyt megtestesítő értékpapír. A kötvénykibocsátó kötelezettséget vállal arra, hogy a kötvénytulajdonosnak (hitelező) előre rögzített, a névértékre vonatkoztatott kamatlábnak megfelelő nagyságú kamatot fizet, és a kötvény lejártakor, vagy előre meghatározott időpontokban a kötvény névértékét visszafizeti. Jellemzői:        Névérték: A kötvénykibocsátó adóssága Kibocsátási árfolyam: Általában névértéken bocsátanak ki

egy kötvényt. Piaci érték: A kötvényből származó pénzáramlások jelenértéke (elméleti árfolyam). Aktuális piaci árfolyam: az az árfolyam, amelyen a kötvényekkel a másodlagos piacokon kereskednek. Lejárat: Az az időpont, amikorra a névérték teljes egészében visszafizetésre kerül. Névleges kamatláb: A kötvény névértékére vonatkozóan megállapított évi kamatláb. Tőketörlesztési szerkezet: Mikor és milyen formában fizeti vissza a névértéket? A kötvények árfolyama: Pn C3 Cn C1 C2 P0 = + + + . + + 2 3 n n 1 + r (1 + r ) (1 + r ) (1 + r ) (1 + r ) Csak a jövőbeli Cash-flow számít!  Eredeti futamidő vs. Hátralévő futamidő  1)Lejáratkor egy összegben fizető kamatszelvényes kötvény: Pn 1 1  P0 = C ⋅ 1 − + n n r  (1 + r )  (1 + r )  Pl: Egy vállalat 2000.0924-én egy 20100924én lejáró 10000 Ft névértékű, 10%-os névleges kamatlábú kötvényt bocsátott ki. A kamatok évente (év

végén) esedékesek, a névértéket lejáratkor fizetik vissza. Mennyit kell fizetni a kötvényért 2005.0924-én, ha az aktuális piaci kamatláb 8%? 1  1  10000 1 10803 + = P0 = 1000 ⋅ − 5 5   0,08  1,08  1,08  Mennyit fizetünk a kötvényért, ha a piaci kamatláb 12%? ( 1,12 ) = 1000 5 P0 − 1 10000 + = 9725 5 5 0,12 ⋅1,12 1,12  Ha r > i => P0 < Pn  Ha r < i => P0 > Pn  Ha r = i => P0 = Pn 2) Lejáratkor egy összegben fizető, nem állandó kamatszelvényes kötvény:  A névleges kamatláb előre rögzített feltételek mellett változhat Cn Pn C1 C2 P0 = + + . + + 2 n n 1 + r (1 + r ) (1 + r ) (1 + r ) 3) Kamatszelvényes kötvény, nem lejáratkor egyösszegű törlesztéssel  A tőketörlesztés üteme előre rögzítve van Lehet:  állandó ütemű  Halasztott (türelmi idő)  Nem állandó ütemű  Arra kell ügyelni, hogy a kamat mindig csak a hátralévő

(nem törlesztett) tőkerészletre jár! Pl:  Egy 5 év futamidejű, 10000 Ft-os névértékű kötvény évente 15% kamatot fizet. A kötvény névértékét egy év türelmi idő után négy egyenlő részletben fizetik vissza. A kötvény kibocsátása óta két év telt el. A piaci hozam 12% Mennyi a kötvény reális árfolyama (P0)? 3625 3250 2875 P0 = + + = 7873 , 9 2 3 1,12 1,12 1,12 Örökjáradékos kötvény:   A kibocsátó állandó kamat fizetését vállalja az idők végtelenéig, de a névértéket nem kell visszafizetnie. Pl: Mennyi a reális árfolyama annak a 10000 Ft névértékű lejárat nélküli kötvénynek, amely évente 6% hozamot fizet, ha a piaci kamatláb 8%? 600 P0 = = 7500 0,08 5) A kötvények nettó és bruttó árfolyama  Pbruttó = Pnettó + felhalmozódott kamat Felhalmozódott kamat = Pn ⋅ i ⋅ n 365 Példa:     Egy 10000 Ft névértékű, 14%-os névleges kamatozású kötvény bruttó

árfolyama június 8án 107,32% volt. A kamatokat évente egyszer, február elsején fizetik. A befektetők által elvárt hozam 12%. Mennyi a kötvény nettó árfolyama? Felhalmozódási idő=28+31+30+31+7=127 nap Felhalmozódott kamat = (10000x0,14x127)/365=487 Ft Pnettó=10732-487=10245=102,45% 6) A kötvények hozama:  Két tényező befolyásolja  Kamatláb A névérték (vagy eladási árfolyam) és a vételi árfolyam különbségéből (árfolyamnyereség)  A kötvényhozamok típusai:  Névleges hozam (kupon ráta) = névleges kamatláb  Egyszerű hozam (szelvény hozam) CY = C tényleges 0 P  Tényleges hozam (lejáratig számított hozam) (YTM) = a belső megtérülési rátával, azzal a megtérüléssel, mellyel a kötvény pénzáramlásait diszkontálva pont a vételi árfolyamot kapjuk.  Pl: Egy 10000 Ft-os névértékű, 16%-os névleges kamatozású kötvényt 7 éves futamidővel négy évvel ezelőtt bocsátottak ki. A

kamatokat évente fizetik, a névérték visszafizetése lejáratkor egy összegben történik. Közvetlenül a kamatfizetés után a kötvényt 104%-os árfolyamon vásárolták meg. A piaci kamatláb 13% volt.   1) Megérte-e megvenni? 2) Mennyi az YTM? P0 = 10708 kamatl PV áb YTM = 13 + 10708 − 10400 (16 − 13) = 14,31 708 13% 10708 YTM 10400 16% 10000 7) Kötvényárfolyamok kamatérzékenyége  Duration: Átlagos hátralévő futamidő  Ct  ⋅t ∑  t t =1  (1 + r )  D= n Ct ∑ t t =1 (1 + r ) n  Képlete: