Gazdasági Ismeretek | Operációkutatás » Egy szállítási feladat megoldása

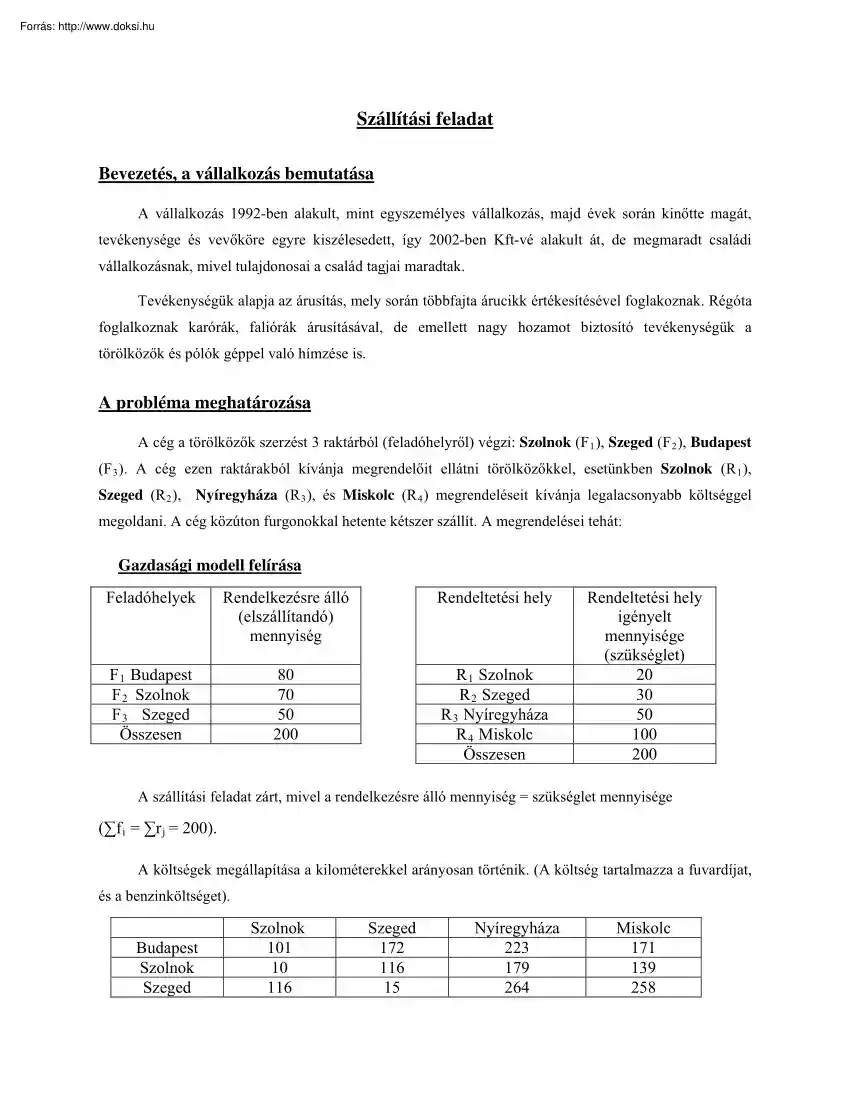
Szállítási feladat Bevezetés, a vállalkozás bemutatása A vállalkozás 1992-ben alakult, mint egyszemélyes vállalkozás, majd évek során kinőtte magát, tevékenysége és vevőköre egyre kiszélesedett, így 2002-ben Kft-vé alakult át, de megmaradt családi vállalkozásnak, mivel tulajdonosai a család tagjai maradtak. Tevékenységük alapja az árusítás, mely során többfajta árucikk értékesítésével foglakoznak. Régóta foglalkoznak karórák, faliórák árusításával, de emellett nagy hozamot biztosító tevékenységük a törölközők és pólók géppel való hímzése is. A probléma meghatározása A cég a törölközők szerzést 3 raktárból (feladóhelyről) végzi: Szolnok (F 1 ), Szeged (F 2 ), Budapest (F 3 ). A cég ezen raktárakból kívánja megrendelőit ellátni törölközőkkel, esetünkben Szolnok (R 1 ), Szeged (R 2 ), Nyíregyháza (R 3 ), és Miskolc (R 4 ) megrendeléseit kívánja legalacsonyabb költséggel megoldani. A

cég közúton furgonokkal hetente kétszer szállít A megrendelései tehát: Gazdasági modell felírása Feladóhelyek Rendelkezésre álló (elszállítandó) mennyiség Rendeltetési hely F 1 Budapest F 2 Szolnok F 3 Szeged Összesen 80 70 50 200 R 1 Szolnok R 2 Szeged R 3 Nyíregyháza R 4 Miskolc Összesen Rendeltetési hely igényelt mennyisége (szükséglet) 20 30 50 100 200 A szállítási feladat zárt, mivel a rendelkezésre álló mennyiség = szükséglet mennyisége (∑f i = ∑r j = 200). A költségek megállapítása a kilométerekkel arányosan történik. (A költség tartalmazza a fuvardíjat, és a benzinköltséget). Budapest Szolnok Szeged Szolnok 101 10 116 Szeged 172 116 15 Nyíregyháza 223 179 264 Miskolc 171 139 258 Kilométerskála alapján a szállítás költsége • 0-50-ig 1 • 50-120-ig 2 • 120-150-ig 3 • 150-200-ig 4 • 200-240-ig 5 • 240-300-ig 6 Rj Fi Budapest Szolnok Szeged Szükséglet Szolnok Szeged

Nyíregyháza Miskolc 2 1 2 20 6 1 9 30 5 4 6 50 4 3 6 100 Elszállítandó mennyiség 80 70 50 200 A szállítási költséget az egyes feladóhelyek és rendeltetési helyek között az alábbi táblázat tartalmazza. Rj Fi F1 F2 F3 szükséglet R1 R2 R3 R4 elszállítandó mennyiség 2 1 2 20 6 1 9 30 5 4 6 50 4 3 6 100 80 70 50 200 A táblázat belső részében költségmátrix van, amelynek az elemei azt mutatják meg, hogy az egyes telephelyről az egyes megrendelőhelyre mennyi pénzegységért szállítják el az áru egy egységét. A célfüggvény felírása K = 2x 11 + 6x 12 + 5x 13 + 4x 14 + 1x 21 + 1x 22 + 4x 23 + 3x 24 + 2 x 31 + 9 x 32 + 6 x 33 + 6x 34 min Az egyenlet A célfüggvény a benne szereplő változóknak csak azon értékeire értelmezhető, amelyek eleget tesznek a következő feltételeknek: x 11 + x 12 +x 13 + x 14 = 80 x 21 + x 22 + x 23 + x 24 = 70 U x 31 + x 32 + x 33 + x 34 = 50 x 11 + x 21 + x 31 = 20 x 12 + x 22 + x 32

= 30 V x 13 + x 23 + x 33 = 50 x 14 + x 24 + x 34 = 100 A szállítási költséget az egyes helyek között az alábbi táblázat tartalmazza ezer db törölközőre vonatkozóan, ezer Ft-ban, táblázatban, majd költségmátrixba. F1 F2 F3 fi R1 2 1 2 20 R2 6 1 9 30 R3 5 4 6 50 R4 4 3 6 100 rj 80 70 50 200 f i : szükséglet az áruból r j : elszállítandó árumennyiség c= 2654 1143 2966 Oszlopredukció Minden oszlopban ki kell vonni a legkisebb elemet az oszlop minden eleméből, így minden oszlopban van legalább egy nulla. F1 F2 F3 fi R1 1 0 1 20 R2 5 0 8 30 R3 1 0 2 50 R4 1 0 3 100 rj 80 70 50 200 Sorredukció Sorredukció szükséges az oszlopredukció elvégzése után, mivel nem minden sorban szerepel nulla érték. F1 F2 F3 fi R1 0 0 0 20 R2 4 0 7 30 R3 0 0 1 50 R4 0 0 2 100 rj 80 70 50 200 A probléma megoldása A probléma megoldása során Vogel-Korda módszert alkalmazunk, azaz soronként és oszloponként a két legkisebb elemet

kivonjuk egymásból, vagyis differenciákat képzünk. Ezután a legnagyobb differencia sorába vagy oszlopába a legkisebb költséghelyre a lehető legnagyobb mennyiséget programozzuk. R1 F1 0 F2 0 0 20 F3 fj R2 R3 4 0 30 20 7 30 diff1 0 4 diff2 0 0 20 1 R4 0 80 0 20 30 2 50 30 100 20 1 2 0 1 2 diff3 0 1 2 diff4 0 1 diff5 0 rj diff1 diff2 80 0 0 0 0 0 0 50 20 200 1 1 1 1 Kötött ismeretlenek száma: m + n – 1 = 4 + 3 – 1 = 6 F1 F2 F3 fi R2 4 0 30 7 30 R3 0 0 20 1 30 50 R4 080 0 20 2 100 rj 80 70 50 200 Szállítási költség K = Kr + Ko + Ks Kr = 0⋅20 + 0⋅30 + 0⋅20 + 1⋅30 + 0⋅80 + 0⋅20 = 30 eFt Ko = 1⋅50 + 1⋅60 + 4⋅40 + 3⋅50 = 420 eFt Ks = 1⋅100 + 1⋅40 = 140 eFt K = 30 + 420 + 140 = 590 eFt diff4 70 40 20 A kapott eredménytáblázat R1 0 0 0 20 20 diff3 diff5 1 Optimális –e a megoldás? Az ellenőrzés potenciálok módszerével történik: a kötött elemek száma ≥ sor + oszlop

- 1 6 ≥ 3 + 4 -1 (Ha nem állna fel az egyenlet, akkor be kellene vinni egy szabad elemet 0 értékű szállítással) kötött elemnél: c ij = u j + v j szabad elemnél: c ij = c ij – (u j + v j ) Vj Ui U1 U2 U3 -1 -1 0 V1 0 0 0 0 20 V2 1 4 0 30 7 V3 1 0 0 20 1 30 V4 1 080 0 20 2 kötött elemnél: ui + vj = c ij u1 + v4 = 0 u2 + v2 = 0 u2 + v3 = 0 u2 + v4 = 0 u3 + v1 = 0 u3 + v3 = 1 szabad elemnél: δij = cij - (ui+vj) δ 11 = 0 – (0-1) = 1 δ 12 = 4 – (1-1) = 4 δ 13 = 0 – (1-1) = 0 δ 14 = 0 – (1-1) = 0 kötöttt elem δ 21 = 0 – (0-1) = 1 δ 22 = 0 – (1-1) = 0 kötött elem δ 23 = 0 – (1-1) = 0 kötött elem δ 24 = 0 – (1-1) = 0 kötött elem δ 31 = 0 – (0+0) = 0 kötött elem δ 32 = 7 – (0+1) = 6 δ 33 = 1 – (0+1) = 0 kötött elem δ 34 = 2 – (0+1) = 1 Ha van negatív elem a táblában, a szállítást javítani kell hurok módszerrel: a javítás úgy történik, hogy ahol negatív volt, azt kötött elemmé kell tenni, tehát egy

kört kell az új taggal és a régi kötött elemekkel alkotni, majd a kör legkisebb értékű szállításával a kör összes szállítását rendre csökkenteni, majd növelni. De mivel nem kaptam negatív elemet az ellenőrzés során, így a szállítási feladat megoldása optimális, vagyis a legkisebb költséggel való szállítást kaptam eredményül. Eredmény gazdasági értékelése Optimális szállítás megvalósulása esetén a költség 590 ezer Ft. Az optimális szállítások • Budapest Miskolc 80.000 db törölköző • Szolnok Szeged 30.000 db törölköző • Szolnok Nyíregyháza 20.000 db törölköző • Szolnok Miskolc 20.000 db törölköző • Szeged Szolnok 20.000 db törölköző • Szeged Nyíregyháza 30.000 db törölköző