Biológia | Állatvilág » Kemencei Zita - Funkcionális válasz

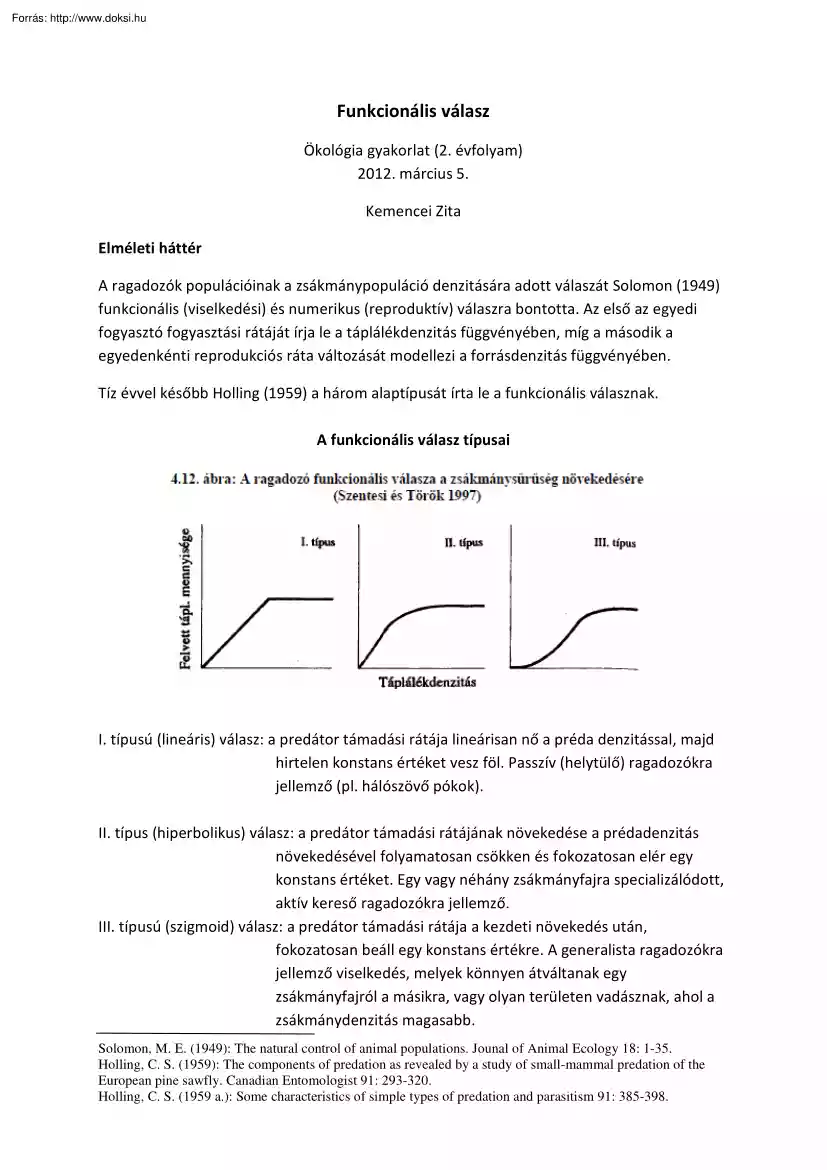
Funkcionális válasz Ökológia gyakorlat (2. évfolyam) 2012. március 5 Kemencei Zita Elméleti háttér A ragadozók populációinak a zsákmánypopuláció denzitására adott válaszát Solomon (1949) funkcionális (viselkedési) és numerikus (reproduktív) válaszra bontotta. Az első az egyedi fogyasztó fogyasztási rátáját írja le a táplálékdenzitás függvényében, míg a második a egyedenkénti reprodukciós ráta változását modellezi a forrásdenzitás függvényében. Tíz évvel később Holling (1959) a három alaptípusát írta le a funkcionális válasznak. A funkcionális válasz típusai I. típusú (lineáris) válasz: a predátor támadási rátája lineárisan nő a préda denzitással, majd hirtelen konstans értéket vesz föl. Passzív (helytülő) ragadozókra jellemző (pl. hálószövő pókok) II. típus (hiperbolikus) válasz: a predátor támadási rátájának növekedése a prédadenzitás növekedésével folyamatosan csökken és

fokozatosan elér egy konstans értéket. Egy vagy néhány zsákmányfajra specializálódott, aktív kereső ragadozókra jellemző. III. típusú (szigmoid) válasz: a predátor támadási rátája a kezdeti növekedés után, fokozatosan beáll egy konstans értékre. A generalista ragadozókra jellemző viselkedés, melyek könnyen átváltanak egy zsákmányfajról a másikra, vagy olyan területen vadásznak, ahol a zsákmánydenzitás magasabb. Solomon, M. E (1949): The natural control of animal populations Jounal of Animal Ecology 18: 1-35 Holling, C. S (1959): The components of predation as revealed by a study of small-mammal predation of the European pine sawfly. Canadian Entomologist 91: 293-320 Holling, C. S (1959 a): Some characteristics of simple types of predation and parasitism 91: 385-398 Korong egyenlet A ragadozók prédadenzitásra adott válaszait modellező egyenletet korong egyenletnek is nevezik, mivel Holling (1959 a.) korongokat használt a prédák

szimulálására Matematikailag a Michaelis-Menten féle enzimkinetikát követő modellről van szó. A modell a ragadozó kétfe tevékenységét veszi figyelembe: (1) a préda keresését és (2) a préda kezelését (vadászattól az emésztésig). A predátor fogyasztási rátája limitált, mert hiába áll annyi préda a ragadozó rendelkezésére, hogy a keresési idő nulla legyen, a kezelés akkor is időt igényel. Tehát a ragadozó összes zsákmányszerzéssel töltött ideje: T=Tsearch+Thandling Ha feltételezzük, hogy a ragadozó T idő alatt Ha zsákmányt ejt, akkor a kezelési idő (Thandling) az elejtett zsákmányok számával arányos: ΣThandling=HaTh ahol Th az egy prédára eső kezelési idő. A zsákmányejtést random folyamatnak tekintjük. A ragadozó az összes zsákmányt elejti az általa egységnyi idő alatt átvizsgált területen (felfedezési terület vagy keresési ráta; mértékegysége 1/időegység). Ha a ragadozó Tsearch időt töltött

el kereséssel akkor ez alatt az időtartam alatt aTsearch területet tud átvizsgálni és aHTsearch zsákmányt ejt. Ha=aHTsearch , így Behelyettesítve az egyenletet: 2 Ha-ra átrendezve az egyenletet az alábbi, a II. típusú funkcionális választ leíró egyenletet kapjuk: Az egyenletből a a Ha=f(H) görbe kiindulási meredekségét, míg T/Th az aszimptotát adja meg. Korong kísérlet: Kellékek: asztal= „vadászterület” korongok = zsákmány stopper óra műanyag edény (a megevett zsákmánynak) Kendő vagy sál (szem bekötéséhez) Csapattagok: a) predátor (bekötött szemmel) b) kezelési időt mérő személy c) az egyperces „futamot” mérő személy A prédaszám állandóságáért felelős személy lehet „c” vagy „d”. A predátor az asztalon vadászik, EGY UJJAL! CSAK TAPOGATNI LEHET, nem szabad az ujjhegyet az asztalon csúsztatni. Ha zsákmányt talál két ujjal veheti föl és a műanyag edénybe teszi (ez modellezi a kereséséi

időt), majd újra keresni kezd. Kísérlet menete: 1. c) indítja az időmérést, amit hangosan jelez, ezzel egyúttal a kísérlet is indul, 2. amikor a) zsákmányt ejt b) indítja az órát, 3. amíg a beteszi a korongot az edénybe b) méri az időt, 4. c) vagy d) új korongot helyez az asztalra, amíg a) az elejtett zsákmányt (=korongot) a műanyag edénybe teszi, 5. a) új keresésbe kezd (ujja ismét megérinti az asztalt) b) megállítja az órát (DE NEM NULLÁZA LE! Ő mérei az összes kezelési időt (ΣTh)), 6. c) jelzi az 1 perc és ezzel együtt a kísérlet végét Denzitásonként 3-3 ismétlés. Vizsgált denzitások: 4, 10, 60, 150 Válasz típusonként és denzitásonként kitöltendő táblázatok: 3 Futam 1. 2. 3. Átlag Ha ΣTh Th Hallgatói csoportok átlagainak összesítésére: H Ha ΣTh Th 4 10 60 150 Eltérés az egyes funkcionális válaszok modellezésében II. típusú funkcionális válasz: a préda elhelyezkedése a területen random,

minden prédaegyed egyedül (nem csoprotokban) helyezkedik el. I.típusú funkcionális válasz: a kezelési idő nagyon alacsony (Th>0) ezért az egyenlet nevezője 1-hez közelít. A grafikonon egy a meredekségű egyenes kell látszódjon A modellezéshez a kísérlet menetét módosítjuk: • amikor a) zsákmányt talál, jelzi ezt a cserélő személynek (c) vagy d)), aki kicseréli a zsákmányt, miközben a) tovább keres III. típusú funkcionális válasz: a zsákmány menedékbe húzódását csoportos eloszlással modellezzük, így a ragadozó megtanulja a zsákmány elhelyezkedését. Kis denzitásnál a hatékonyság, míg a denzitás növekedésével a kezelési idő limitál. A modellezéshez a kísérlet menetét módosítjuk: • a zsákmányt csoportokban kell elhelyezni az asztalon. Minél nagyobb a denzitás, annál nagyobb csoportokat hozunk létre. Kísérlet kiértékelése: Ábrázolni a felvett táplálék mennyiségét a táplálékdenzitás

függvényében, illetve a kezelési időt az elejtett zsákmány számának függvényében. 4