Informatika | Információelmélet » A JPEG veszteséges képtömörítő

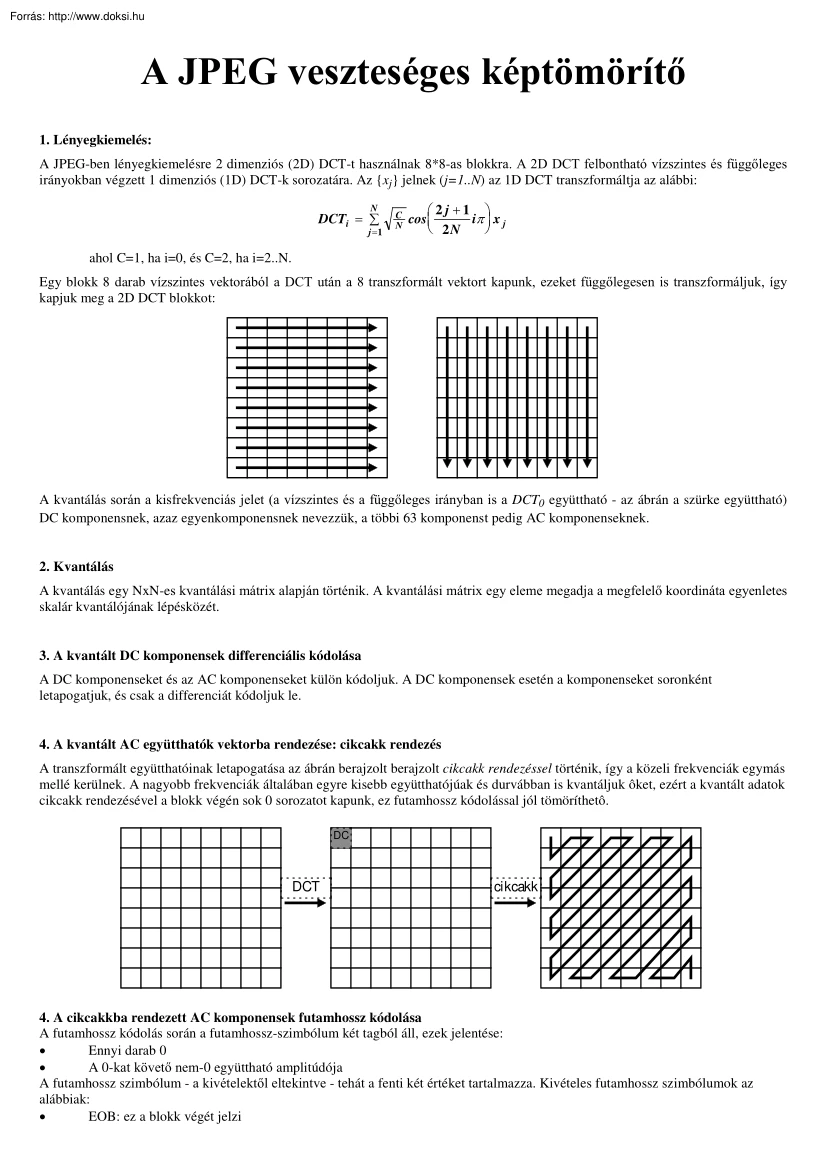
A JPEG veszteséges képtömörítő 1. Lényegkiemelés: A JPEG-ben lényegkiemelésre 2 dimenziós (2D) DCT-t használnak 8*8-as blokkra. A 2D DCT felbontható vízszintes és függőleges irányokban végzett 1 dimenziós (1D) DCT-k sorozatára. Az {xj} jelnek (j=1N) az 1D DCT transzformáltja az alábbi: N DCTi = ∑ j =1 C N 2j +1  iπ  x j cos  2N  ahol C=1, ha i=0, és C=2, ha i=2.N Egy blokk 8 darab vízszintes vektorából a DCT után a 8 transzformált vektort kapunk, ezeket függőlegesen is transzformáljuk, így kapjuk meg a 2D DCT blokkot: A kvantálás során a kisfrekvenciás jelet (a vízszintes és a függőleges irányban is a DCT0 együttható - az ábrán a szürke együttható) DC komponensnek, azaz egyenkomponensnek nevezzük, a többi 63 komponenst pedig AC komponenseknek. 2. Kvantálás A kvantálás egy NxN-es kvantálási mátrix alapján történik. A kvantálási mátrix egy eleme megadja a megfelelő koordináta egyenletes skalár

kvantálójának lépésközét. 3. A kvantált DC komponensek differenciális kódolása A DC komponenseket és az AC komponenseket külön kódoljuk. A DC komponensek esetén a komponenseket soronként letapogatjuk, és csak a differenciát kódoljuk le. 4. A kvantált AC együtthatók vektorba rendezése: cikcakk rendezés A transzformált együtthatóinak letapogatása az ábrán berajzolt berajzolt cikcakk rendezéssel történik, így a közeli frekvenciák egymás mellé kerülnek. A nagyobb frekvenciák általában egyre kisebb együtthatójúak és durvábban is kvantáljuk ôket, ezért a kvantált adatok cikcakk rendezésével a blokk végén sok 0 sorozatot kapunk, ez futamhossz kódolással jól tömöríthetô. DC DCT cikcakk 4. A cikcakkba rendezett AC komponensek futamhossz kódolása A futamhossz kódolás során a futamhossz-szimbólum két tagból áll, ezek jelentése: • Ennyi darab 0 • A 0-kat követő nem-0 együttható amplitúdója A futamhossz

szimbólum - a kivételektől eltekintve - tehát a fenti két értéket tartalmazza. Kivételes futamhossz szimbólumok az alábbiak: • EOB: ez a blokk végét jelzi • ESC szimbólumok: ekkor a fenti két értéket adott bitszámon követi a bitfolyamban ezt a szimbólumot - ez a szimbólum csak a gyakoriságfüggő kódolás egyszerűsítése miatt van lásd később) Példa: Kódoljuk le az alábbi kvantált blokkot: 0 0 0 0 0 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 DC 0 1 0 2 0 0 64 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 A példablokk cikcakk rendezésére A cikcakk rendezés után kapott sorozat: {1,0,0,1,2,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,64,0,.,0} Ennek a futamhossz kódolása: <0,1><2,1><0,2><0,-1><16,64><EOB> 5. Gyakoriságfüggő kódolás A futamhossz szimbólumokhoz egy Huffman kód kódszavai vannak hozzárendelve. Mivel a 0 futam hossza 0-tól 62-ig

változhat (6 biten írható le), illetve a kvantált együttható is 8 bites, így a futamhossz szimbólumokhoz egy 2 amelynek sok eleme valószínűleg elő sem fordulna. 14 méretű táblázatot kellene csatorni, Emiatt a következő egyszerűsítást vezették be: a leggyakoribb futamhossz szimbólumokhoz rendelnek hozzá Huffman kódot, és csinálnak néhány speciális szimbólumot, amely után külön bitszámon meg kell mondani a futamhossz szimbólum két értékét. Például a fenti példa Huffman-kódolása az alábbi (informatív értékekkel): Szimbólum Huffman kódszó indexe <0,1> <2,1> <0,2> <0,-1> <16,64> 3 12 7 4 nincs ilyen, helyette ESC1 és a 16 és 64 kiírása 8-8 bittel 0 <EOB> Huffman kódszó bitmintája 1001 11100101 110001 10001 az ESC1 mintája: 11111111110 00 A csatornára írt bitek 1001 11100101 110001 10001 11111111110 000010000 01000000 00