Fizika | Felsőoktatás » Fizika példatár

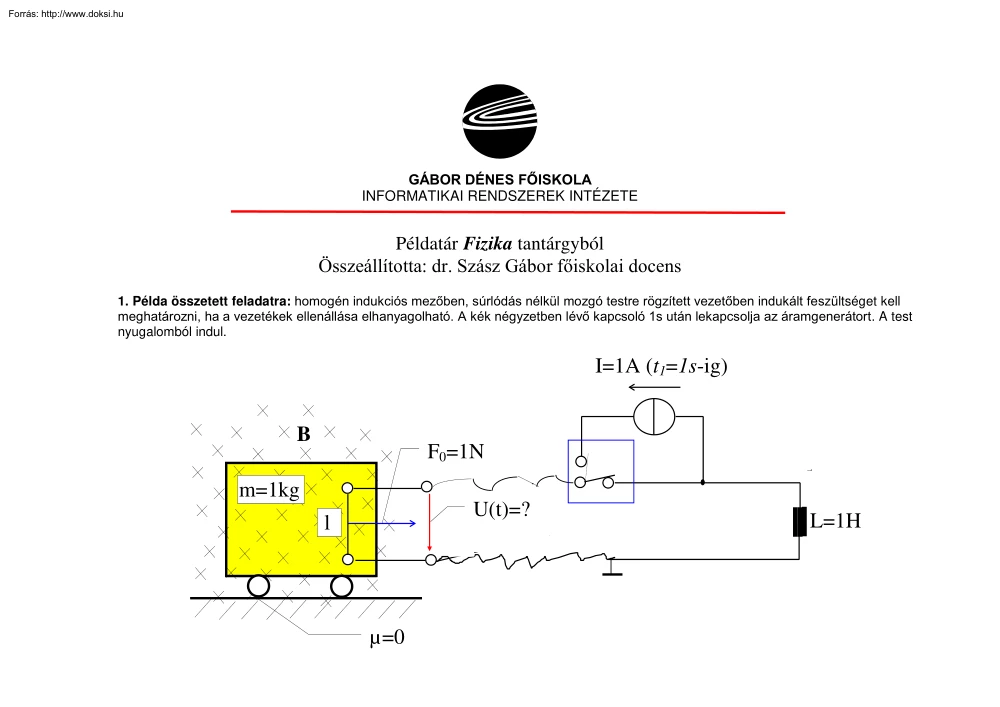
GÁBOR DÉNES FŐISKOLA INFORMATIKAI RENDSZEREK INTÉZETE Példatár Fizika tantárgyból Összeállította: dr. Szász Gábor főiskolai docens 1. Példa összetett feladatra: homogén indukciós mezőben, súrlódás nélkül mozgó testre rögzített vezetőben indukált feszültséget kell meghatározni, ha a vezetékek ellenállása elhanyagolható. A kék négyzetben lévő kapcsoló 1s után lekapcsolja az áramgenerátort A test nyugalomból indul. I=1A (t1=1s-ig) B F0=1N m=1kg U(t)=? l µ=0 L=1H Kidolgozás: F = BIl  Vs  ⇒ Bl = 1 U = Bvl  m F m a = =1 2 m s (kezdetben) m v = a ⋅ t ⇒ v1 = a ⋅ t1 = 1 , ha v0 = 0. s A feszültség 1 másodperc alatt 1V-ra növekszik. A villamos töltés: Q1 = I ⋅ t1 = 1Cb Éppen így viselkedik az 1F kapacitású kondenzátor A kapcsoló zárása után ( t ≥ t1 ) a rendszer az alábbi modellel helyettesíthető: C=1F L=1H Ez egy rezgőkör, melynek saját körfrekvenciáját Thomson kép1 ω = = 1 s −1 lete

alapján lehet meghatározni: LC [ ] Az első másodpercben u(t) grafikonja egy origón átmenő, egységnyi meredekségű egyenes. Ezután pedig egy Ux amplitúdójú, egységnyi körfrekvenciájú szinuszos jel: U ( t ) = U x sin( t + ϕ ), ha t ≥ t1 Tudjuk, hogy t1-nél a jel értéke és meredeksége is egységnyi: Ez éppen 1.  U x sin(1 + ϕ ) = 1   U x cos(1 + ϕ ) = 1 U x2 [sin 2 (1 + ϕ ) + cos2 (1 + ϕ )] = 2 ⇒ U x = ± 2[V ] tg(1 + ϕ ) = 1 ⇒ 1 + ϕ = π 4 ± k ⋅π π 5π ⇒ 1 + ϕ1 = 1 + ϕ2 = 4 4 Most már felírható a megoldás képlete:    ( ) U t =    0, t, ha t < 0 ha 0 ≤ t < 1 π  2 sin  t − 1 +  , ha t ≥ 1  4 A megoldás grafikonja: t[ s] 0 2. példa Forgó mozgás esetén, pl. egy szinkron motor üresjáratban, szintén kapacitásként terheli a villamos hálózatot, tehát javíthatja a fázistényezőt. Lássunk erre egy példát (Dr Pattantyús Ábrahám Géza:

Gépek üzemtana c. könyvéből)! Egy U=500V-os f=50Hz periódusú, váltakozó feszültségű, kétvezetékes (egyfázisú) hálózatból 150m távolságra, - tehát L=300m távolságú és A=16mm2 keresztmetszetű vörösréz vezetéken keresztül - villamos energiát viszünk át egy műhelybe, ahol két, egyenként P=11kW-os motor üzemel. A korszerűbb motor hatásfoka: η1=90%, teljesítménytényezője: cosϕ1=0,88; a másik motor hatásfoka: η2=0,84% és cosϕ2=0,78. Az első motor felvett teljesítménye: P 11 P1 = = = 12,2[ kW] η1 0,9 P1 12200 = ≅ 27,7[ A] , I1 = U ⋅ cos ϕ1 500 ⋅ 0,88 Az áramfelvétele: amely két komponens eredője: I1P = I1 ⋅ cos ϕ1 ≅ 24,4[ A] és I1r = I1 ⋅ sin ϕ1 ≅ 13,2[ A] . A másik motorra ugyanígy kiszámíthatóak a megfelelő villamos P 11 P2 13100 [ ] = ≅ 13 1 , kW I = = mennyiségek: , 2 U ⋅ cos ϕ2 500 ⋅ 0,78 ≅ 33,6[ A] , η2 0,84 I2 P = I2 ⋅ cos ϕ2 ≅ 26,2[ A] és I2 r = I2 ⋅ sin ϕ2 ≅ 21[ A] . P2 =

A vezeték feszültségesését ∆U=25V-ra korlátozzuk. A vezeték ellenállása = 0,0182 ⋅ pedig: ρ = 0,0182 300 ≅ 0,314[Ω] , 16 Ωmm2 m L R = ⋅ = ρ fajlagos ellenállás esetén A a megengedhető legnagyobb áramerősség ∆U 25 = ≅ 73[ A]〉 I1 + I 2 ≅ 61,3[ A]. I= R 0,341 A különbséget felhasználhatjuk világításra. Pl 100W-os izzóból beköthető: n≤ UIi 100 , ahol I i = I − ( ∑ I r ) − ∑ I P = 732 − 34,2 2 − 50,6 ≅ ≅ 64,5 − 50,6 = 13,9[ A] , tehát n = eredője: tg ϕ m = ∑ Ir ∑ IP = 2 2 500 ⋅ 13,9 ≅ 69db. 100 34,2 ≅ 0,676 ⇒ ϕ m ≅ 34  50,6 A teljesítménytényező ⇒ cos ϕ m ≅ 0,83 . IP  Ii { ∑I P I ϕm 0 Ir ∑ Ir Ha bekötünk a hálózatba egy üresen járó szinkronmotort, amely előállítja az indukciós motorok számára szükséges meddő teljesítményt, akkor a teljesítménytényező eredője 1 lesz. A szükséges meddő teljesítmény: QSr = U ⋅ ∑ I r =

500 ⋅ 34,2 = 17100[VAr ] A szinkron motor üresjáratban felvett Ii irányú áramát az üresjárási teljesítményből (PSp=1660W) lehet kiszámítani: I SP PSP 1660 = = ≅ 3,3[ A] U 500 Ilyenkor a világításra felhasználható áramerősség: I i = I − ∑ I P − I SP = 73 − 50,6 − 3,3 = 19,1[ A] , az izzólámpák lehetséges száma pedig: 95. Matematikai levezetés a teljesítménytényező és az effektív értékek magyarázatához Fél periódusra számított átlagteljesítmény, mint a p=ui pillanatnyi teljesítmény integrál-középértéke: p = u ⋅ i = U sin ωt ⋅ I sin(ωt − ϕ ) T P= 2 T 2 ∫ 0 T  2π  sin pdt = t ⋅ sin  t − ϕ  dt = ∫  T  T 0 T  2UI 2 2π T 2π 2π   t ⋅ sin t cos ϕ − cos t sin ϕ  dt = sin = ∫ T 0 T T T    2UI 2 2π 4π T T t   2 1 − cos  2 UI 2UI 2 2π 2π T t cos t sin ϕdt = cos ϕdt − sin = ∫ ∫ T 0 T T 2 T 0 =

  cos ϕ UI 2  UI 2π  sin ϕ sin + T π  T 2 t  = U ⋅ I ⋅ cos ϕ , 0  0 ahol U= U 2 és I = I 2 az effektív értékek. 3. példa: Egy légvédelmi ágyú csövének deformációját kell megm = 1000 v határozni. Tudjuk, hogy a lövedék torkolati sebessége: s , radian a lövedék tömege: m=2kg, az ágyúcső szögsebessége: ω = 2 s , a cső hossza l=3m, másodrendű nyomatéka nem állandó: cm4 I = 25 ⋅ (16m − x) és az anyagára jellemző rugalmassági modulus: m E = 2 ⋅ 10 7 N cm2 . Fontos szilárdságtani összefüggés van a hajlító nyomaték és az ún. rugalmas szál görbülete között: M ( x) y′′ 2 = , g ( x) = ahol y általában elhanyagolható az 1 mellett. ′ 2 EI ( x) 1 + y′ A hajlító nyomaték a következő ábra alapján írható fel: y F x l-x l M ( x) = − F ( l − x) = F ( x − 3) A rugalmas szál differenciálegyenlete: F ( x − 3) x − 16 + 13  13  y

′′ ≅ 1 A = ⋅ A = −  , 8  16 − x  16 − x 5 ⋅ 10 (16 − x) 2mvω 8 ⋅ 10 3 F −1 , 0 16 ahol A = m = = = [ ] 4 4 4 5 ⋅ 10 Coriollis-erő 5 ⋅ 10 5 ⋅ 10 A másodrendű differenciálegyenlet integrálása után megkapjuk a rugalmas szál meredekségét (a szögelfordulás tangensét): 16   y′ ≅ A[ − 13 ln(16 − x) − x] + c = A13 ln − x, mert 16 − x   y′( 0) = 0 ⇒ c = 13 Aln 16 A cső torkolatának szögelfordulása: 16  16    y ′( l ) = A13 ⋅ ln − 3 = 0,1613 ⋅ ln − 3 = −0,04811 = tg ∆ϕ   13  13  ⇒ ∆ϕ = −2°45′ 16 ′′ 1000m távolságon ez kb. 48m-nyi eltérést jelent, ami céltévesztést okoz, ha nem korrigálják Tehát ez a számítás fölhasználható a lőelemképzéshez, vagy a löveg szögsebességének korlátozásához. A legkisebb hatás elve, avagy a természet „lustasága” Például egy ferde hajítás során olyan

pályagörbe mentén halad az elhajított test, amelyre nézve az energiák különbségének időintegrálja minimális. Ez képletben a következő: t2 t2 t1 t1 ( ) I = ∫ ( Em − Eh )dt = ∫ L q, q, t dt , legyen min{ I } Ez nem hagyományos szélsőérték-feladat, hiszen egy q(t) skalár-vektor függvénnyel leírható pályagörbéhez minimális értéke. I-t funkcionálnak nevezzük, és azt matikai módszert, amellyel a feladatot megoldják számításnak hívják. E szerint I akkor minimális, ha optimális tartozik I a matevariáció- d ∂L ∂L = , dt ∂ q i ∂ qi Pl. L = mv2 2 pl. q1 = x, q1 = vx , q2 = y és q2 = v y − mgh, ahol v 2 = vx2 + v 2y és h = y ∂L ∂L ∂L ∂L = 0, = − mg, = mvx és = mv y ∂x ∂y ∂ vx ∂ vy d ( mvx ) = 0 ⇒ mvx = const. x − irányú egyenlet: dt d mv y = − mg y − irányú egyenlet: dt ( ) 4. példa: Síkbeli ferde hajítás légellenállással v Súlypont Fe G=mg F e = − ce ρ 2 v

⋅ v ⋅ A, ahol ∆x     x  lim ∆ t v =   =  ∆t 0 ∆y   y    lim ∆t 0 ∆t   A gyorsulás meghatározása komponensenként: x   a =  , y   v = x 2 + y 2 ρ  x = − ce A v ⋅ x 2m t t 0 0 ⇒ x (t ) = ∫  x(ξ ) dξ + x (0) ⇒ x(t ) = ∫ x (ξ ) dξ + x(0) t t ρ  y = − ce A v ⋅ y − g ⇒ y (t ) = ∫ y(ξ )dξ + y (0) ⇒ y(t ) = ∫ y (ξ )dξ + y(0) 2m 0 0 Numerikus integrátorokkal, digitális szimuláció módszerével oldjuk meg a feladatot a TUTSIM program segítségével. Összes mechanikai energia Mozgási energia Látszik, hogy a közegellenállás hatására a pályagörbe aszimmetrikussá válik, a röppálya magassága és távolsága is csökken, a becsapódás szöge növekszik, a mechanikai energiák összege viszont csökken. 5. példa: Egy folyó átlagos sebessége  m

5  . s A folyó sebességét vízlépcső alkalmazásával Egy szállító hajó, melynek a vízhez viszonyított átlagos sebessége  m 10   , s  m 2   -ra s lassítják. ingajáratban közlekedik a folyó 300 km-es szakaszán. A zsilipelés időszükséglete 5140” Mennyi a megtakarított idő a vízlépcsőzés előtti helyzethez képest? Kidolgozás: A zsilipelés ideje: tzs=60·51+40=3100[s]  m w = ± 10 A relatív sebességek: 1, 2  s   m v = 5  s A szállító sebességek:  m vzs = 2  s A folyón történő elmozdulások: s1, 2 = ±300[ km] A ciklusidők: 3 ⋅ 10 5 3 ⋅ 10 5 t1 = + = + = 8 ⋅ 10 4 [ s] w1 + v w2 + v 15 5 s1 s2 3 ⋅ 10 5 3 ⋅ 10 5 t2 = + = + = 62500[ s] w1 + vzs w2 + vzs 12 8 s1 s2 Az időkülönbség: ∆t = t1 − t 2 − t zs = 80000 ′′ − 62500 ′′ − 3100 ′′ = 14400 ′′ = 4 h . Tehát a vízlépcsőzés négy

órával csökkenti a fuvarozás ciklusidejét.  m  m 6. feladat: Egy folyó átlagos sebessége 3   A folyó sebességét vízlépcső alkalmazásával 1   -ra lassítják s s Egy szállító hajó, melynek a vízhez viszonyított átlagos sebessége  m 9 , s ingajáratban közlekedik a folyó 240 km-es szakaszán. A zsilipelés időszükséglete 40 Mennyi a megtakarított idő a vízlépcsőzés előtti helyzethez képest? Megoldás: 1h. 7. példa Instacionárius áramlás vizsgálata Egy nagyméretű tartályból kiáramló folyadék sebességének meghatározása a veszteségtaggal kiegészített, instacionárius Bernoulli-egyenlet alapján: 1 h A>>a A tartály keresztmetszete sokkal nagyobb, mint a csőé. Ezért h≈const. Egy áramvonal mentén integrálunk. 2 l Az instacionárius Bernoulli-egyenlet: ∂v ρ   dl +  pst + ρ gh + v 2  + ∆p ′ = 0, ∂t 2 1  1 l ρ 2 ahol ∆p′

= λ v csősúrlódási veszteség ( nyomásesés) d 2 λ = f ( Re) csősúrlódási tényező d a cső átmérője ρ a folyadék sűrűsége ∂v lokális gyorsulás, amely a tartályban elenyésző ∂t v a térfogatáram és a keresztmetszet hányadosa 2 ρ∫ 2 Ha összenyomhatatlan a folyadék, akkor a lokális gyorsulás a cső mentén azonos, ami egyszerűsítést tesz lehetővé: l dv ρ 2  v ρl + 1 + λ ⋅  = ρ gh d dt 2  dv  1 λ  v2 gh + +  = dt  l d  2 l dv ∫ gh  1 λ  v2 = t + c − +  l l d 2 l dv 2 = t +c ∫ l v gh   1 − 1 + λ ⋅   d  2 gh l d + λl αdv = t + c, ahol α = ghα ∫ 1 − (αv) 2 2 ghd Sikerült egy ún. alapintegrálra visszavezetni a feladat megoldását 2d l arth(α v) = t + c gl ( d + λ l ) α gh t+k arth(α v) = l e x − e− x  α gh  t + k th x = x − x és lim th x = 1 α v = th  x∞  l  e +e  α gh  t + k v( t ) = th 

 α  l 1 Ha v( 0) = 0, akkor v( t ) = v( ∞) = k = 0. 2 ghd  gh( d + λ l ) t  th  ⋅  d + λl  l 2d   2 ghd 1 = d + λl α Az áramlási sebesség diagramján jól követhető a tranziens jelenség. Az áramlási sebesség folyamatosan csökkenő meredekséggel v( ∞) -hez tart. 8. példa Egyenes körhenger alakú rúdból korongokat készítenek esztergapadon ún leszúró késsel A forgó korong egy vályúba hullik, és azután saját perdületének egy része lendületté alakul, majd tovagördül. A kezdeti mechanikai energia hányad része alakul hővé? ω0 d v FS Kidolgozás: Amíg a korong csúszik, a súlypontját a súrlódó erő gyorsítja: súlypont sebessége: FS FS = µmg a = = µ g . Ezért a m v = a ⋅ t = µ gt . A súrlódó erő nyomatéka ugyanekkor szöggyorsulást okoz (a szögsebesség abszolút értékét csökkenti, mert sgn ω 0 = −1 ). A tárcsa tehetetlenségi nyomatéka: Θ = mr 2 2 = md 2 8 ,

tehát a szöggyorsulás: µ mgd 4µ g ∆ω M 2 β = = = = md 2 d ∆t Θ 8 ω = ω0 + β ⋅ t = ω0 + 4µ g d ⋅t . v1 = − r ω1 = µ gt1 , tehát a két módon számított sebesség egyenlősége alapján: 2 µ gt1 4 µ gt1 − = ω0 + d d d ω0 − d ω0 = 6 µ gt1 ⇒ t1 = − 6 µg ω0 dω0 ⇒ v1 = 6 µ gt1 = − ⇒ ω1 = A gördülés kezdetén 6 3 A mozgási energia egy része hővé alakul. A kezdeti mozgási energia: Θω 02 md 2 ω 02 E0 = . = 2 16 Θω12 md 2ω02 md 2ω02 + = A gördülés pillanatában érvényes mozgási energia: E1 = 2 + 2 = 72 144 mv12 = md 2ω 02 48 . 2 2 ω md 1 1 2   0 2 2 ω = − = − = = ⋅ E0 Q E E md   0 1 0 A keletkezett hőmennyiség:  16 48  24 3 9. feladat Az előző példához hasonlóan, egy forgó korongot helyezünk egy vízszintes felületre A korong súlypontja fölgyorsul. a. Meg kell határozni a súlypont sebességét az idő függvényében: v(t)=? b. A tiszta gördülésig mennyi

hő keletkezik a súrlódás miatt? Adatok: a tárcsa átmérője a tárcsa tömege a tárcsa kezdeti szögsebessége a súrlódási tényező a nehézségi gyorsulás d = 1 [m] m = 2 [kg] ω0= -10 [s-1] µ = 0,2 g = 9,81 [ms-2] Megoldás: t1 ≅ 0,85[ s]  m v1 ≅ 1,67  Q ≅ 8,3[ J ] s v v1 m 1 s t O t1 1s 2s 10. példa Egy villamos kondenzátor körlap alakú fegyverzetének sugara: r=3 cm, a fegyverzetek közti távolság: d=0,1 mm, a rést kitöltő dielektrikum relatív permittivitása pedig εr=4. Mekkora a kondenzátor kapacitása? Kidolgozás: A r 2π , C = ε ⋅ = εr ε0 ⋅ d d ahol ε a permittivitás (dielektromos állandó) és F   m a vákuumbeli permittivitás, 4 9 ⋅10 − 4 π −9 ⋅ = tehát C = 10 [ F ] = 1nF . −4 9 4π ⋅ 9 ⋅10 10 1 ε0 = 4π ⋅ 9 ⋅109 11. példa Két koncentrikus egyenes körhengerből álló villamos kapacitás hossza: l=25 cm, a külső és a belső D átmérő viszonya: k =

1,2 , a köztük lévő rést εr=4 permittivitású dielektrikum tölti ki. Mekkora a Db kondenzátor kapacitása? Kidolgozás: 2πε r ε 0 l 2π ⋅ 4 ⋅ 0,25 1 l = = C = 2πε ⋅ = ≅ 3,05 ⋅ 10 −10 [ F ] = 305 pF 9 9 D D 4π ⋅ 9 ⋅ 10 ln 1,2 18 ⋅ 10 ln 1,2 ln k ln k Db Db 12. példa Az ábrán látható kapcsolási rajz egy váltakozó áramú villamos hálózatot ábrázol, melyben egy feszültségforrás, két ellenállás, egy kapacitás és egy önindukciós tekercs található. Állandósult állapotban mekkora amplitúdójú és fázisszögű áram folyik az R2-vel jelölt ellenálláson keresztül? U ( t ) = U 0 sin ωt R1 L i=? iL C U ~ R2 ( ) Kidolgozás: A megoldást a következő alakban keressük: i( t ) = I 0 sin ω t + ϕ Kirchhoff első törvénye (a csomóponti törvény) szerint a kondenzátor árama: iC=i-iL. Kirchhoff második törvénye (a huroktörvény) szerint: iC  =U R1iL + jωLiL +  jωC 2 = −1). j j , ahol a

képzetes egység (  iC = 0 R2 i −  jω C iL = ( CR2 jω + 1)i, melyet az első egyenletbe helyettesítve kapjuk: R1 ( CR2 jω + 1)i + jωL( CR2 jω + 1)i + R2 i = U [ ] R2 (1 − LCω 2 ) + R1 i + jω ( L + CR1 R2 )i = U i 1 = , s áttérve az amplitúdókra: 2 U R2 (1 − LCω ) + jω ( L + CR1 R2 ) i ⋅U0 = I0 = U R (1 − LCω 2 2 ) U0 2 2 + ( L + CR1 R2 ) ω 2 2 , A fáziskülönbség pedig: L + CR1 R2 )ω (  i ϕ = arc  = − Ar ctg  U R2 (1 − LCω 2 ) 13. példa Két proton tömegénél fogva vonzza, töltésénél fogva pedig taszítja egymást Melyik a nagyobb erőhatás? Ez hányszorosa a másiknak? −19 −27 Fizikai adatok: egy proton tömege m = 1,67 ⋅ 10 kg , villamos töltése Q = 1,6 ⋅ 10 Cb, a gravitációs 2 2 1 −11 Nm 9 Nm = 9 ⋅ 10 . állandó f = 6,67 ⋅ 10 kg 2 és a Coulomb-törvényben szereplő állandó 4πε 0 Cb 2 Kidolgozás: Fgrav −64 2 2 −54 ⋅ 5 , 55 10 Nm [ ] m2 ⋅ 1 , 67 10 −11 =

f ⋅ 2 = 6,67 ⋅ 10 ⋅ = 2 r r r2 Q 9 ⋅10 ⋅1,6 ⋅10 = 2 = r2 4πε0 r 2 Fvill 9 2 −38 = [ 2,3 ⋅10−28 Nm2 r2 ] , tehát a villamos kölcsönhatás sokkal nagyobb, mint a gravitációs, bár még ez is elképesztően kis erő a hétköznapi, vagyis makroszkopikus erőkhöz viszonyítva. A két erő aránya: Fvill = 4,1 ⋅ 10 35 . Fgrav 14. példa Mekkora gyorsítófeszültség hatására érheti el az elektron a vákuumbeli fénysebesség 90%-át? 8 m −31 Fizikai adatok: az elektron nyugalmi tömege m0 = 9,1 ⋅ 10 kg , a fény sebessége kb. c = 3 ⋅ 10 s Kidolgozás: A fénysebesség közelében már nem lehet eltekinteni a mozgó tömeg sebességtől való függésétől. Az elektromos erőtér által végzett munka az elektron teljes E=mc2 energiájának megváltozásával egyenlő. A mozgó elektron tömegét m-mel jelöljük Képlettel kifejezve: W = ∆E teljes Q ⋅ U = mc 2 − m0 c 2 , m0 ahol m = 2  v 1−    c A két

összefüggés alapján a feszültséget kifejezhetjük:     −31 2 16 m0 c  1  9,1 ⋅10 ⋅ 9 ⋅10 − 1 = U= −19  2 ⋅ Q , 1 6 10  1 −  v    c   = 511875 ⋅1,2941573 ≅ 662447 [V ] ≅ 662 kV   1 ⋅ − 1 = 2   1 − 0,9 15. példa Tudjuk, hogy a rádium felezési ideje 1600 év Egy bizonyos mennyiségű rádium hányad része bomlik el 800 év alatt? Kidolgozás: a bomlás sebessége arányos a meglévő atomok mennyiségével. Tömeggel kifejezve ez képletben a következő: dm = − χ ⋅ m, ahol χ a bomlási állandó. dt m t dx ∫m x = − χ ∫0 dy 0 m m0 m m = − χt ⇒ ln ≡ = − χt ln log 2 e m0 m0 m t = − log 2 e ⋅ χt = − log 2 m0 T log 2 t − m = 2 T , ahol T a felezési idő. m0 A keresett arány képletben kifejezve: t 800 − − m0 − m m 1 T 1600 = 1− = 1− 2 = 1− 2 = 1− ≅ 0,2929, m0 m0 2 tehát 800 év alatt a rádium kb. 30 %-a

elbomlik 16. Egy 235-ös tömegszámú urán izotóppal működő atomreaktor teljesítménye P=100 MW Tudjuk, hogy egy uránmag hasadásakor EU= 200 MeV energia szabadul fel. a. Határozzuk meg a maghasadás ütemét, vagyis az időegység alatt elbomlott atomok számát! b. Határozzuk meg azt az időt, amely alatt a reaktorba eredetileg töltött 250 kg uránból 10 kg elbomlik? Kidolgozás: a. 10 8 W P ∆N 18 −1 = = = ⋅ , 3 13 10 s [ ] ∆t EU 2 ⋅ 10 8 ⋅ 1,6 ⋅ 10 −19 J b. Az előző példában látszott, hogy a radioaktív bomlástörvény exponenciális függvénnyel írható le, azonban 4%-os csökkenés esetén a bomlás sebessége jó közelítéssel még állandónak tekinthető, tehát egyszerűsítéssel élünk a megoldás során. Tudjuk, hogy 235 g uránban 6 ⋅ 10 23 10000 atom van. Egyenes arányosság alapján 10000 g-ban 235 ⋅ 6 ⋅10 23 = 2,5532 ⋅10 25 darab uránatom van. Ennyi atom elbomlásához szükséges idő kb: 2,5532 ⋅ 10 25 6 [

s] ≅ 3 hónap . t≅ , = ⋅ 8 16 10 18 3,13 ⋅ 10 17. példa Egy négyütemű, hathengeres benzinmotor műszaki leírásában azt találjuk, hogy a g motor fajlagos fogyasztása: , a sűrítési viszony pedig ε=1:6. A benzin fűtőértéke LEh g alapján tudjuk, hogy 100%-os hatásfok esetén a fogyasztás 63 LEh lenne. A munkaközeg 160 adiabatikus kitevője κ=1,35. a. Mekkora a motor effektív hatásfoka? b. Mekkora a helyettesítő, ideális Ottó-körfolyamat termikus hatásfoka? Megoldás: 63 ⋅ 100% a. ηeff = ≅ 39,4% b. ηOtto = (1 − ε κ −1 ) ⋅ 100% ≅ 46,6% 160 18. példa Egy állandó keresztmetszetű csőben nitrogén gáz áramlik A csövet fűtik A belépő m = 40 w ϑ1 = 0C és a nyomása p1 = 1 MPa , a kilépő gáz hőközeg sebessége 1 , a hőmérséklete s mérséklete ϑ2 = 900  C . Az állandó nyomáson mért közepes fajhő 1kg közegre vonatkoztatva J  ,  kg  c p = 1040  J  = 297 R a gázállandó pedig N

 kgK  . Mekkora a kiáramló gáz nyomása és sebes2  sége? Mennyi hőt kell ehhez közölni a gázzal?  Kidolgozás: Fölírjuk a folyamatra érvényes fizikai törvényeket leíró egyenleteket. Áramló közeg esetén az energia-megmaradás törvénye sajátos formában írható fel, mert a belső energia mellett az ún. betolási és kitolási munkákat, valamint a mozgási energia megváltozását is figyelembe kell venni, amikor a hőt kiszámítjuk, de a mechanikai munkákat és a belső energia megváltozását együttesen is számba vehetjük, ha az állandó nyomáson vett fajhővel számolunk. Így jutunk el energia egyenlethez, amely egységnyi tömegre vonatkozik: w12 2 + c p T1 + q12 = w22 2 + c p T2 , (1) J  ahol q12 az egységnyi tömegre jutó hőmennyiség  .  kg  Érvényes a folytonosság tétele is, melyet a fajtérfogat segítségével írunk fel: w1 w2 = v1 v2 ( 2) Feltételezzük az egyesített gáztörvény

érvényesülését is: p1 v1 p 2 v2 = =R T1 T2 ( 3) Az impulzus-tétel mindig érvényes. Kihasználjuk a keresztmetszet állandóságát az egyenlet felírásakor: w12 w22 − + = p1 − p 2 v1 v2 ( 4) A (2) és a (4) egyenlet összevonásával kapjuk, hogy w1 w2 − w1 ) = p1 − p2 , ( v1 a (2) és (3) fölhasználásával pedig w1 w2 p 2 = v1 RT2 w1 RT2 w1T2 p1 ⇒ p2 = = , v1 w2 T1 w2 melyet a fenti egyenletbe helyettesítve, és figyelembe véve ismét, hogy v1 = RT1 , p1 a nitrogén gáz kilépő sebességére az alábbi másodfokúra vezető egyenletet kapjuk:  wT  w1 p1 1 2 w2 − w1 ) = p1 1 −  ( RT1  w2T1  RT1w2 /⋅ w1 p1  RT1  w −  w1 +  w2 + RT2 = 0, melynek megoldásrendszere: w1   2 2 2 w2 =  RT1 RT1  w1 + ±  w1 +  − 4 RT2 w1 w1   2 = 297 ⋅ 27315 , ,   297 ⋅ 27315 40 + , ±   − 4 ⋅ 297 ⋅117315   40 40 = = 2 2 2068,1388 ± 1698,0859 = = 2  m w2 +

≅ 1883  s  m w2 − ≅ 185  s A nagyobb sebesség kifejezhető a Mach-szám segítségével is, amely megmutatja, hogy a kialakuló sebesség hányszorosa a helyi hangsebességnek. A helyi hangsebesség:  m a 2 = κRT2 = 1,4 ⋅ 297 ⋅ 1173,15 ≅ 698,4 , s 1883 tehát a Mach - szám: M ≅ ≅ 2,7. 698,4 A folyamat megvalósulásához szükséges nyomások: 6 ⋅ ⋅ wT p 1 40 117315 10 1 , 1 2 1 ⋅ = ⋅ ≅ 91235[ Pa ] ≅ 912[ hPa ]; p2 + = T1 w2 + 27315 1883 , 6 wT p 1 40 117315 10 1 ⋅ , ⋅ 1 2 1 p2 − ⋅ = ⋅ ≅ 928626[ Pa ] ≅ 0,929[ MPa ]. T1 w2 − 27315 185 , A közölt hőmennyiség fajlagos értékei: 1883 + 40) ⋅ (1883 − 40) J   MJ  ( w22+ − w12 + c p (T2 − T1 ) = + 1040 ⋅ 900 = 2708044,5  ≅ 2,7  q1, 2+ = ; kg kg 2 2     q1, 2− = w22− − w12 2 + c p (T2 − T1 ) = J   MJ  225 ⋅145 . + 936000 = 952312,5  ≅ 0,95  2  kg

  kg  Mindkét hőmennyiség nagyobb, mint az állandó nyomáson végbemenő állapotváltozásé: q1, 2 p  kJ  = c p ( T2 − T1 ) = 936 .  kg  Az eltérő végnyomásokhoz tartozó két hőmennyiség közti eltérésnek a kisebb nyomás során kialakuló, hangsebesség fölötti áramlási sebesség az oka, mert a csőben keletkező lökéshullám „táplálása” nagy energia-felvétellel jár