Elektronika | Felsőoktatás » Zajok jellemzői

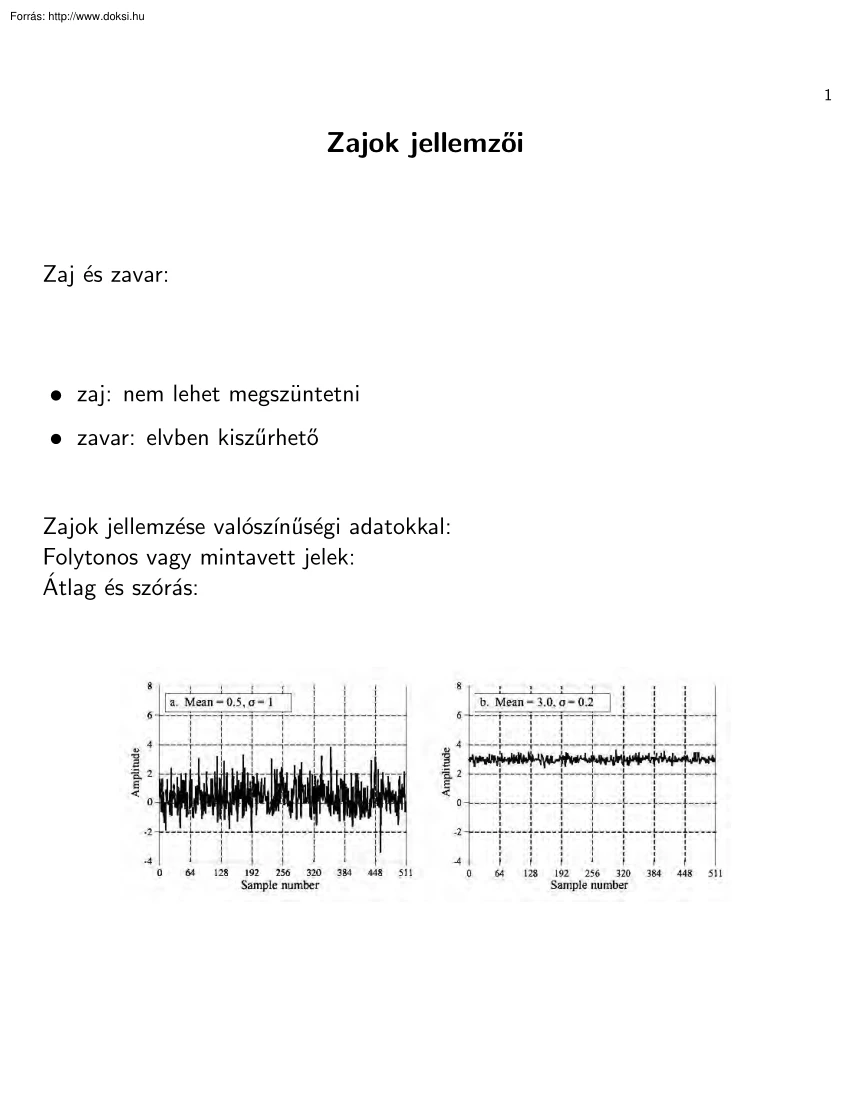
1 Zajok jellemzői Zaj és zavar: • zaj: nem lehet megszüntetni • zavar: elvben kiszűrhető Zajok jellemzése valószı́nűségi adatokkal: Folytonos vagy mintavett jelek: Átlag és szórás: 2 Zaj: effektı́v érték értelmes: λ egyenáramú jel + σ szórású Gauss eloszlású zaj a jel teljesı́tménye: Z ∞ 2 2 2 teljesı́tmény = (λ + x) G(x)dx = λ + σ = P= + P∼ −∞ A jel teljesı́tménye az egyen- és váltakozóteljesı́tmények összege! Ha λ = 0, a teljesı́tmény a szórásnégyzettel egyezik meg Fehérzaj: teljesı́tménysűrűség adott B sávszélességű fehér zaj teljesı́tménye: Pzaj = n0B . . 3 Integráló voltmérő Ha sokáig mérünk: kiátlagoljuk a jelet Milyen lesz ez a súlyfüggvény? T idejű integrálás + delta függvény T ideig integrálva: A súlyfüggvény: T széles impulzus Ha a bemenő zaj B sávszélességű és P

teljesı́tményű volt, akkor a kimeneti zaj: Pzaj = 2 σki = n0Bef f 2 σbe BT . Integráló voltmérők integrálási ideje általában a hálózati feszültség periódusidejének egészszámú többszöröse! 4 Kváziperiodikus jelek mérése zaj jelenlétében Ötlet: Nemperiodikus jelek tegyük kváziperiodikussá! Ezután integrálás/összegezés kisebb zaj. Fázis fontos - vagy pontos fázismérés, vagy saját trigger: 5 τ időközönként k-szor minta, N -szer megismételve: 6 Milyen lesz a jel/zaj viszony? Hasznos jel amplitudóját N -szeresére növeli N-szeresére növekszik a zaj teljesı́tménye (szórásnégyzete) √ jel/zaj javulás mértéke arányos N -vel! ů ÿ jel zaj 1mérés ů ÿ jel zaj Nmérés ÿ ů jel zaj javulás = = = v(i) √ σ2 N v(i) √ N σ2 1 √ N 7 Macska + trigger: 64 átlagolás után sokkal jobb a jel! Összegezés/átlagolás:

milyen lesz a frekvenciatartományban? N db egymást T időközzel követő delta frekvenciaspektruma: V (ω) = N −1 e−iωT N − 1 1 X −iωT e = N n=0 N (e−iωT N − 1) = 1 1 − e−iωT N eiωT N/2e−iωT /2 ( )( )( iωT N/2 −iωT /2 ) = N 1 − e−iωT e e 8 = =⇒ 1 i2 sin(ωN T /2) N i2 sin(ωT /2) |V (f )| = 1 sin(πf N T ) . N sin(πf T ) Minták számának növelése fésűszerű karakterisztika: 9 Minták számának növelése fésűszerű karakterisztika: fésűs szűrő Pl.: 2OO Hz-es négyszögjel + 2OO.1 Hz-es szinusz: 16OOO összegezés után csak a négyszögjel marad! 10 Ismert jelalak amplitudójának mérése Előzetes információ: ismerjük a jelalakot. Mekkora az amplitúdó? 11 t szélességű négyszögimpulzus + fehérzaj: keressük az amplitudót egy H ideális aluláteresztő szűrővel: H sávszélességének növelése: jel amplitudója egy darabig

nő, majd állandó H sávszélességének növelése: zaj amplitudója H -val arányosan nő Optimum?! 12 Bemenőjel alakja ismert: milyen legyen az optimális H a maximálisan pontos amplitúdó méréshez? S/N = Signal/Noise ratio = jel/zaj viszony maximuma h(t) függvényében R∞ 2 [ v(τ )h(t − τ )dτ ] S 0 −∞ R∞ = N n0 −∞ h2(τ )dτ 13 R∞ 2 [ v(τ )h(t − τ )dτ ] S 0 −∞ R∞ = N n0 −∞ h2(τ )dτ Ez maximális, ha h(t) = v(t0 − t) ! Ez az u.n illesztett szűrő Megvalósı́tás digitális szűrővel! Hálózat frekvenciakarakterisztikája: h(t) = v(t0 − t) ! 14 Mennyire optimális? τ szélességű impulzus + B sávszélességű aluláteresztő Jel/zaj az ideális esethez képest rosszabb Az ideális aluláteresztő szűrő kevésbé érzékeny az impulzus szélességére 15 Illesztett szűrő: Bemenőjel két Dirac-delta, relatı́v amplitúdóarány ismert

Milyen az optimális hálózatot ? Két jel + zaj egyetlen mérésből A Hálózat egyszerű digitális (FIR) szűrő + β paraméter: 16 S N ∂ ∂β ţ S N (n + βnT ) 2 = (A + Aαβ)2 n20(1 + β)2 = A2 (1 + αβ)2 n20 1 + β 2 ű ⇒ = 2 β=α 2 2 n + 2βnnT + β nT 17 szélsőérték: β = α 18 Wiener szűrés Dekonvolúció: H(ω) hálózat K(ω) = 1/H(ω) korrekció Probléma a zaj, és a H(ω) = 0 szakasz! Vki(ω) = Vbe(ω)H(ω) z(t) a mérés során megjelenő zaj Mérjük a vz (t) = vki + z(t) jelet ! Optimális K(ω) szűrő: mért Vz (ω) szűrve + dekonvolválva H(ω)-val a legjobban közelı́ti Vbe-t V (ω) = Vz (ω)K(ω)/H(ω) 19 Z ∞ 2 | V (ω) − Vbe(ω) | dω −∞ minimális! Z ∞ 2 | (Vki(ω) + Z(ω))K(ω)/H(ω) − Vki(ω)/H(ω) | dω −∞ Zaj és jel korrelálatlan keresztszorzatuk eltűnik: Z ∞ −2 | H(ω) | 2 2 2 2 (| Vki(ω) | | 1 − K(ω) | + |

Z(ω) | | K(ω) | )dω −∞ Minimális, ha K(ω) minden ω -ra minimális. Deriválva K(ω) : 2 2 2 K(ω) =| Vki(ω) | /(| Vki(ω) | + | Z(ω) | ) Optimális Wiener szűrő 20 Ahol Vki(ω) sokkal nagyobb, mint Z(ω) ≈ 1 ahol a zaj teljesı́tménye sokkal nagyobb kb. a jel/zaj viszony négyzetével esik Vki A Wiener szűrő nem tartalmazza a rendszer súlyfüggvényét, csak a zaj és a jel teljesı́tményspektrumát! Optimális szűrő kell a zaj teljesı́tményspektruma Pl.: Z(ω) = konstans Nagyobb pontosság: elég Z(ω) durva megadása a Wiener-szűrő másodrendben tartalmazza Vki-t és Z -t! Zajos eredeti kép Fourier-transzformált 21 Wiener-szűrő szűrt kép 22 Főkomponens analı́zis Mérési adatok dimenziós vektor φi ortonormális (φiφj = δij ) bázis: X= n X yiφi = ΦY i=1 itt Φ = [φ1 . φn] és Y = [y1 yn]T Az ortonormalitás miatt yi = φiX Y X elforgatottja φi:

tulajdonság, yi méri Keressük m(< n) olyan φ-t, amelyik X-et legjobban közelı́ti! Y nem használt tagjait (előre meghatározandó) bi konstansokkal helyettesı́tjük: X̂(m) = m X i=1 yiφi + n X i=m+1 biφi 23 Minimalizálás χ2 eltérés-négyzet 2 χ = = EkX − X̂(m)k E n X n X T (yi − bi)(yj − bj )φi φj i=m+1 j=m+1 = n X E(yi − bi) 2 i=m+1 E(): várható érték operátor Minimum: deriválni kell χ2-t bi szerint! bi = E yi. Ezt visszaı́rva χ2-be: χ 2 = n X E(yi − E[yi]) 2 i=m+1 = n X T i=m+1 = n X i=m+1 T φi E(X − E[X])(X − E[X]) φi T φi ΣX φi 24 ΣX az adatok kovariancia mátrixa! Bebizonyı́tható, hogy φi-re az optimum ΣX φi = λiφi φi a λi sajátértékhez tartozó sajátvektor 2 χ = n X λi i=m+1 Azt az eredményt kaptuk tehát, hogy a (a χ2 közelı́tés értelemben) Legjobb lineáris reprezentáció: kovariancia mátrix sajátvektorai

szerinti ortogonális transzformáció alapján! Ha i monoton csökken, λi ≥ λj , ha i > j m(< n) fő” komponens minimalizálja az eltérést! ” 25 A φ1 és φ2 sajátvektorok az eloszlás fő tengelyei λ1 és λ2 sajátértékek: φ1 és φ2 mentén az eloszlás varianciája Mivel yi = φTi X, ezért y1 és y2 lesz X vetületei φ1 és φ2 tengelyekre. 26 A yi tulajdonságok ha töröljük az yi tulajdonságot, akkor a közelı́tés hibája λi-vel nő meg. Veszteséges tömörı́tés: csak a legnagyobb m sajátkomponenst és az arra vett vetületek alapján! Visszaállı́tás: átlagos eltérés értéke n X λi i=m+1 ha lesz. Ha ez sokkal kisebb, mint m X λi i=1 , és m sokkal kisebb, mint n, akkor jelentős tömörı́tés! Egyes tulajdonságok egymástól függetlenek: yi egymás közötti korrelációja 0. Adatok entrópiájára is szélsőérték: az összes lineáris

transzformáció közül ez a transzformáció minimalizálja a transzformációk Y terében mért entrópiamaximumot (minimax viselkedés)! Stacionárius idősorok + főkomponens analı́zis 27 yi tulajdonság-függvényei ejωit alakúak ! Visszakapjuk a Fourier-transzformációt! Főkomponens analı́zis hátrányai: nem mindig (fizikailag) értelmes levonni E[X]-t Csak lineáris tulajdonságok! Ellenpélda: adott sı́kban körı́vet leı́ró adatok Ezt a hátrányt az adatok Normalizálás: xi adatok kxk szerint normálva a főkomponens analı́zis rendben végrehajtható! Pn zi = xi/ j=1 xj normálás ΣX szinguláris!