Agricultural science | Studies, essays, thesises » Csapadékmaximum-függvény számítása

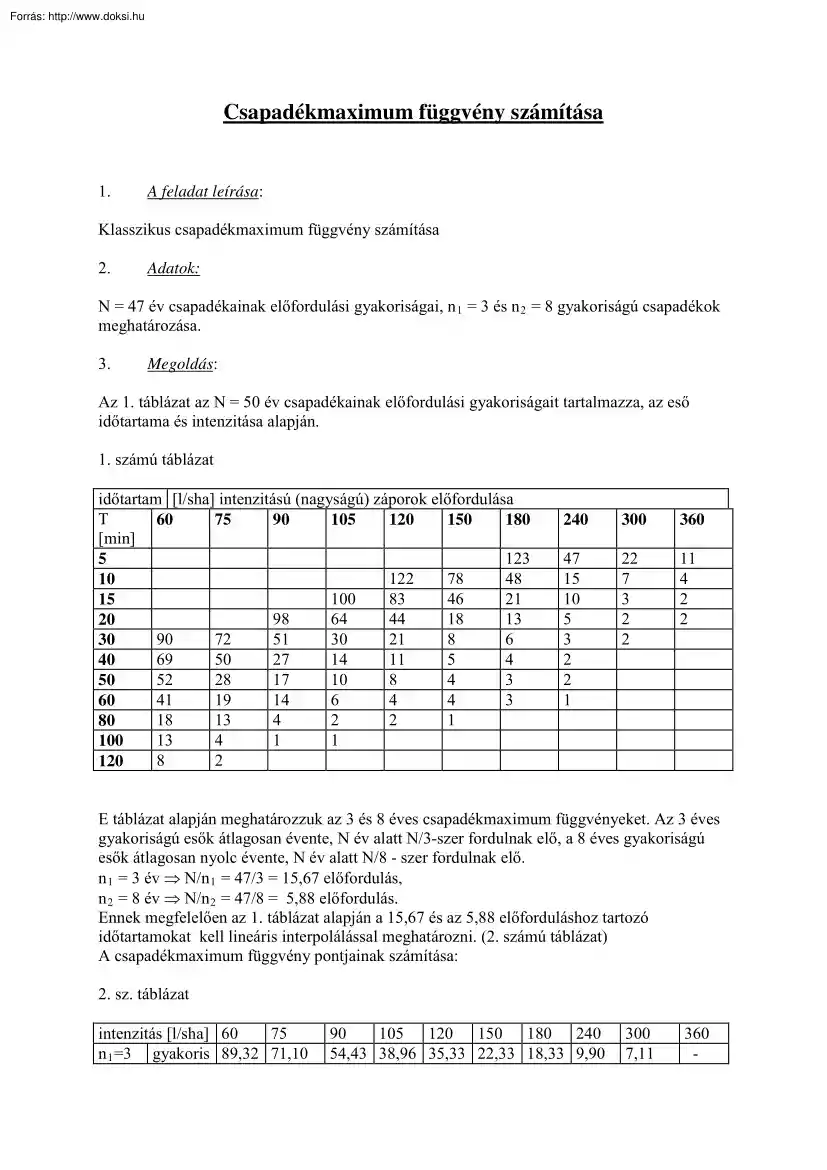
Csapadékmaximum függvény számítása 1. A feladat leírása: Klasszikus csapadékmaximum függvény számítása 2. Adatok: N = 47 év csapadékainak előfordulási gyakoriságai, n 1 = 3 és n 2 = 8 gyakoriságú csapadékok meghatározása. 3. Megoldás: Az 1. táblázat az N = 50 év csapadékainak előfordulási gyakoriságait tartalmazza, az eső időtartama és intenzitása alapján. 1. számú táblázat időtartam [l/sha] intenzitású (nagyságú) záporok előfordulása T 60 75 90 105 120 150 180 [min] 123 5 122 78 48 10 100 83 46 21 15 98 64 44 18 13 20 90 72 51 30 21 8 6 30 69 50 27 14 11 5 4 40 52 28 17 10 8 4 3 50 41 19 14 6 4 4 3 60 18 13 4 2 2 1 80 13 4 1 1 100 8 2 120 240 300 360 47 15 10 5 3 2 2 1 22 7 3 2 2 11 4 2 2 E táblázat alapján meghatározzuk az 3 és 8 éves csapadékmaximum függvényeket. Az 3 éves gyakoriságú esők átlagosan évente, N év alatt N/3-szer fordulnak elő, a 8 éves gyakoriságú esők átlagosan nyolc évente, N év

alatt N/8 - szer fordulnak elő. n 1 = 3 év ⇒ N/n 1 = 47/3 = 15,67 előfordulás, n 2 = 8 év ⇒ N/n 2 = 47/8 = 5,88 előfordulás. Ennek megfelelően az 1. táblázat alapján a 15,67 és az 5,88 előforduláshoz tartozó időtartamokat kell lineáris interpolálással meghatározni. (2 számú táblázat) A csapadékmaximum függvény pontjainak számítása: 2. sz táblázat intenzitás [l/sha] 60 75 n 1 =3 gyakoris 89,32 71,10 90 105 120 150 180 240 54,43 38,96 35,33 22,33 18,33 9,90 300 7,11 360 - n 2 =8 ágú esők időtarta ma 95,82 76,24 60,60 55,30 37,07 30,60 19,12 11,40 8,66 A táblázatban szereplő adatokat aritmetikus és szemilogaritmikus koordináta rendszerben kell ábrázolni. A szemilogaritmikus ábrázolás esetén a függvény grafikonja két párhuzamos egyenes, melyeknek az egyenletét kell meghatározni a meredekségük és az egyperces időtartamhoz tartozó csapadék intenzitása alapján. -m = b/c = 0,55/0,90 = 0,61 a 1 = 1100 l/sha a 2 = 1480

l/sha 4. i 1 = a 1 x T -m = 1100 T -0,61 3 éves gyakoriság esetén i 2 = a 2 x T -m = 1480 T -0,61 8 éves gyakoriság esetén. Megállapítás: m <0, azaz a csapadékmaximum függvény mindig degresszív, tehát n - szeres időtartam alatt statisztikus n - szeresnél mindig kevesebb mennyiségű, azaz az eredetinél kisebb intenzitású csapadék várható. 5. Irodalomjegyzék: Kontur István, Koris Kálmán, Winter János: HIDROLÓGIAI SZÁMÍTÁSOK Akadémiai Kiadó, Budapest, 1993 Dr. Koris Kálmán: HIDROLÓGIAI SZÁMÍTÁSI SEGÉDLET Tankönyvkiadó, Budapest 1992