Language learning | English » Exponential and logarithm functions

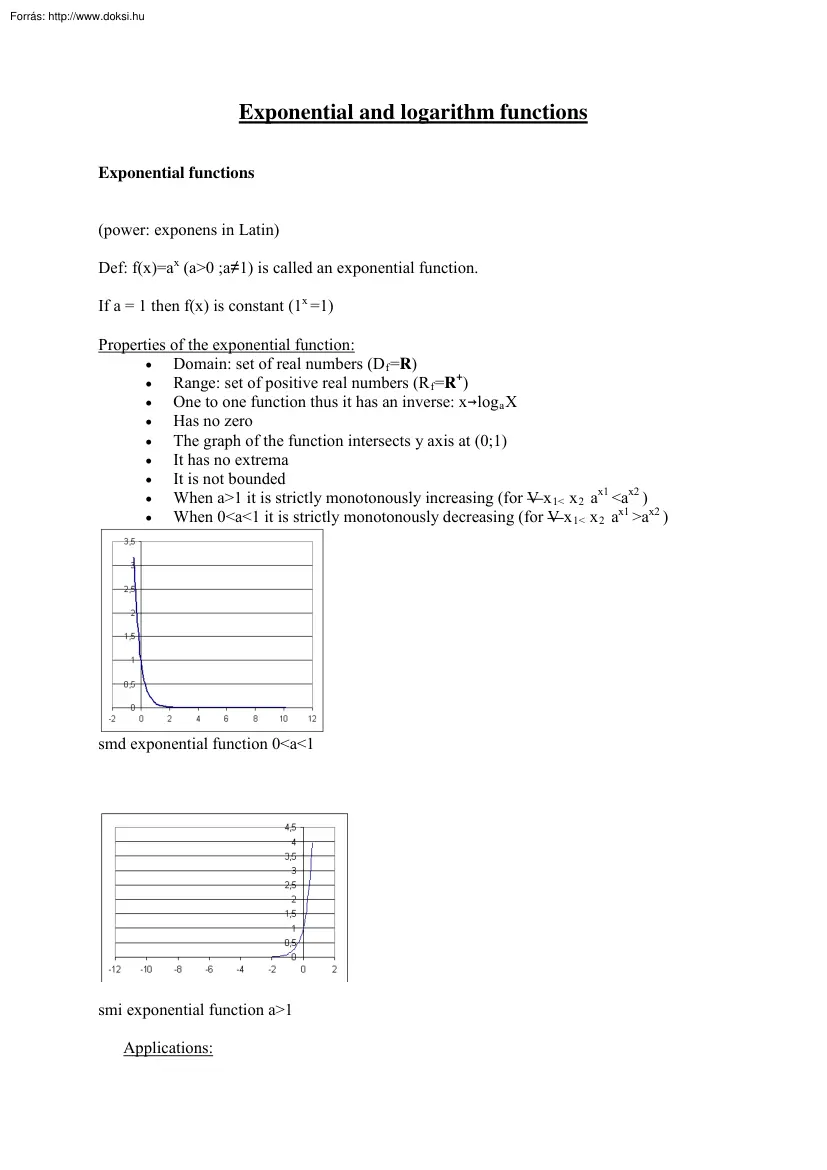
Exponential and logarithm functions Exponential functions (power: exponens in Latin) Def: f(x)=ax (a>0 ;a≠1) is called an exponential function. If a = 1 then f(x) is constant (1x =1) Properties of the exponential function: • Domain: set of real numbers (D f =R) • Range: set of positive real numbers (R f =R+) • One to one function thus it has an inverse: xlog a X • Has no zero • The graph of the function intersects y axis at (0;1) • It has no extrema • It is not bounded • When a>1 it is strictly monotonously increasing (for V x 1< x 2 ax1 <ax2 ) • When 0<a<1 it is strictly monotonously decreasing (for V x 1< x 2 ax1 >ax2 ) smd exponential function 0<a<1 smi exponential function a>1 Applications: • Compound interest (kamatos kamat) • Pressure (nyomás számítás) • Hangintenzitás • Oldódási idő Logarithm Def: The log a b is a unique real exponent, indicating the power to which the base must be raised to produce the

number b while b>0 ; a>0 ; a≠1 (alogab =b) Properties of function: • Domain: set of positive real numbers (D f =R+) • Range: set of real numbers (R f =R) • It is a one to one function thus it has an inverse function (x ax) • Zero: x=1 • The graph of the function intersects the x axis at point (1;0) • When a>1 it is smi • When 0<a<1 it is smd • It has no extrema a>1 smi log function log a 1=0 log a a=1 Identities: 1. log a bc=log a b+log a c 2. log a (b/c) = log a b-log a c 3. log a bn=nlog a b 4. log a b= log c b/ log c a Theorem: log a bc=log a b+log a c Proof: 1. alogabc=bc ↑ by definition 2. alogab+logic =alogab x alogac=bc ↑identities for power 0<a<1 smd log function logabc ↓↓ logab+logic =a ↕ because f(x)= ax is smi log a bc=log a b+log a c a Q. e d