Egészségügy | Biofizika » Röntgen sugárzás keletkezése, abszorpciója, röntgen krisztallográfia

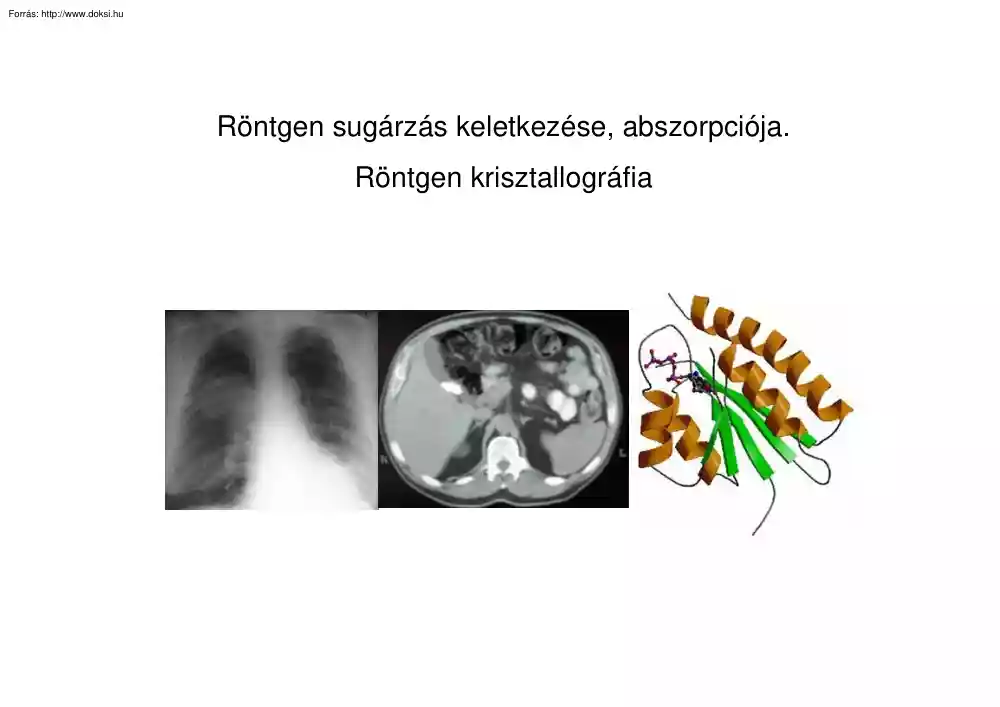
Röntgen sugárzás keletkezése, abszorpciója. Röntgen krisztallográfia Röntgensugárzás előállítása + - anód fűtött katód (elektronforrás) röntgensugarak (fékezési+karakterisztikus) Fékezési röntgensugárzás keletkezése gyorsított elektronok anód (antikatód) röntgenfoton gyorsított elektron E foton = hf + Ekin = 1 2 mv 2 atommag Az atommag által eltérített elektron 1 2 Ekin = mv mozgási energiája megváltozik a 2 mozgási energiaváltozásnak megfelelő energia fotonná alakul 1 2 1 mv − mv2 = hf 2 2 intenzitás Fékezési röntgensugárzás spektruma 20 kV 1. Miért nem egy éles csúcs a spektrum? Mert az elektron több lépésben véletlenszerű eloszlásban adja le az energiáját. 2. Miért csökken a határhullámhossz növekvő feszültség esetén? Mert növekszik az elektron maximális kinetikus energiája. hf1 = 10 kV λ 10 kV λmin, 20min, kV hf 3 = 1 1 2 2 mv1 − mv2 2 2 λ 1 1 2 2 mv4 − mv3 2 2 + 1 2

mv3 2 1 2 mv4 2 1 2 mv1 2 + hf 2 = + 1 1 2 2 mv2 − mv3 2 2 1 2 mv2 2 fmaxazaz azazλλminakkor akkorészlelhető, észlelhető, fmax min haaz azelektron elektronegy egylépésben lépésben ha lassulle. le. lassul + hf max = 1 2 mv1 = eU 2 intenzitás Karakterisztikus röntgensugárzás keletkezése I. 1. a gyorsított elektron üresedést hoz létre egy belső héjon 25 kV 2. az üresedés egy felső héjról betöltődik 20 kV Kα 3. a két héj közötti energia röntgen foton formájában kisugárzódik: Kβ hf = EL − EK 10 kV λ Ekin 1 2 = mv 2 gyorsított elektron + K L M Karakterisztikus röntgensugárzás keletkezése II. N M L Lα, Lβ K Kα, Kβ, Kγ Auger elektronok keletkezése 1. A gyorsított elektron által létrehozott üresedés egy felső elektronhéjról betöltődik. 2. A betöltődés során felszabaduló energia nem foton formájában sugárzódik ki, hanem egy környező elektron veszi fel, ami elhagyja az atomot. + K

L Gyorsított elektron által létrehozott üresedés M Röntgensugárzás abszorpciója I. I Io 1 0 0.8 -2 I ln Io 0.6 0.4 0.36 0.2 0 0 -4 -6 -8 1/μ 0.5 I = I oe 1 1.5 2 -10 0 A görbe meredeksége: -μ 0.5 1 1.5 x x − μx ha x=1/μ I = e − μx Io I = e −1 = 0.3679 Io A gyengítési tényező annak a távolságnak a reciproka, amely alatt a sugárzás intenzitása e-1 szeresére csökken. 2 ln I = − μx Io Io – belépő intenzitás I – intenzitás az x pontban μ – gyengítési tényező ([μ]=1/m) Röntgensugárzás abszorpciója II. A röntgensugárzás abszopciójához vezető legfontosabb kölcsönhatások: 1. Fotoeffektus: a röntgenfoton teljes kinetikus energiáját átadja az atomnak, ennek hatására egy elektron kilép az atomból. röntgenfoton + K kilökött fotoelektron hf = Ekötési + Ekinetikus L M Röntgensugárzás abszorpciója III. A röntgensugárzás abszopciójához vezető legfontosabb

kölcsönhatások: 2. Compton effektus: A röntgenfoton egy külső elektronnak átadja energiája egy részét. Az elektron kilökődik, a foton kisebb frekvenciával, irányváltozást szenvedve halad tovább. Compton elektron röntgenfoton (f) 1 2 hf = hf + A + me ve 2 + K L M szórt röntgenfoton (f’) Röntgensugárzás abszorpciója IV. A röntgensugárzás abszopciójához vezető legfontosabb kölcsönhatások: 3. Párképződés: a röntgenfoton egy nehéz atommag közelében elektronpozitron párrá alakul elektron Az atommag meglökődik, ezáltal átveszi a röntgenfoton lendületének egy részét. + K L M elektron pozitron hf min = (melektron + m pozitron ) c 2 a foton energiájának fedezni kell az elektron és a pozitron nyugalmi tömegének megfelelő energiát annihilláció: pozitron elektronnal ütközve két gamma fotonná alakul. Röntgendiffrakció I. γ2 γ1 c Δs = c ⋅ cos γ 2 = 2 ⋅ λ Δs = c ⋅ cos γ 1 = 1 ⋅ λ

Röntgensugárzás atomok, ionok, molekulák (szórócentrumok) Δs = c ⋅ cos γ = l ⋅ λ Röntgendiffrakció II. Az útkülönbség ferdén beeső röntgensugárzás esetén γ γ0 Δs1 Δs2 Δs = Δs1 − Δs2 = c(cos γ 0 − cos γ ) Röntgendiffrakció III. Laue egyenletrendszer háromdimenzióban a(cos α 0 − cos α ) = hλ b(cos β 0 − cos β ) = kλ c(cos γ 0 − cos γ ) = lλ cos 2 α + cos 2 β + cos 2 γ = 1 Az egyenletrendszer túlhatározott (3 ismeretlen (a,b,c), 4 egyenlet), megoldást csak speciális esetekben lehet találni. 1. Forgó kristály módszer 2. Porított kristály módszer Röntgendiffrakció IV. Bragg-féle értelmezés α d Δs = 2d cos α Röntgendiffrakció V. Visszaverődés különféle síkokról 2 dimenziós vetület és a síkok jelölése (h,k,l): (1,1,0) síkok (2,1,0) síkok Röntgendiffrakció VI. A síkok jelölése segít távolságuk meghatározásában (2,1,0) síkok h=2 k=1 l=0 b 1 h2 k 2 l 2 = 2+

2+ 2 2 d a b c ha a=b=c: 1 h2 + k 2 + l 2 = 2 d a2 a a/2 d 2d cos γ = λ 2a cos γ h +k +l 2 cos γ = 2 2 =λ λ h2 + k 2 + l 2 2a Mivel a (h,k,l) számok kombinációi nem képesek minden egész számot generálni, az interferencia-mintázatban jellegzetes hiányok mutatkoznak. Ezek a hiányok jellemzőek az adott rácstípusra Röntgendiffrakció VII. Molekulák szerkezetének meghatározása • Az eddigi módszerekkel csak a rácspontok távolságát lehet meghatározni, de pl. molekulák, proteinek szerkezetét nem • Molekulakristályok esetében a rácspontokban maguk a molekulák helyezkednek el, tehát egy rácspont belső szerkezetét kell meghatározni. Δs1 rácspont Δs = Δs1 − Δs2 Δs2 A reflexiók intenzitását befolyásolja a rácspontok struktúrája. Röntgendiffrakció VIII. A hemoglobin háromdimenziós szerkezete