Matematika | Középiskola » Vörös József - Elsőfokú függvények

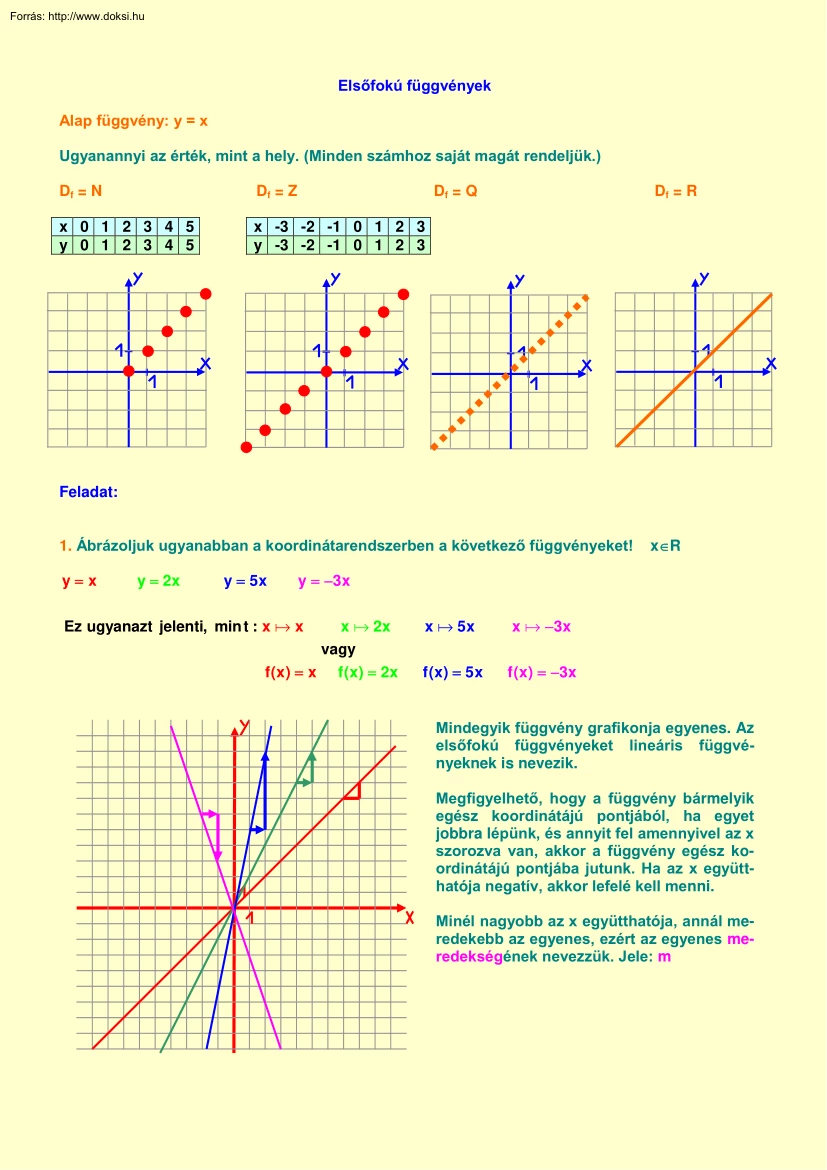
Elsőfokú függvények Alap függvény: y = x Ugyanannyi az érték, mint a hely. (Minden számhoz saját magát rendeljük) Df = N Df = Z Df = Q x 0 1 2 3 4 5 y 0 1 2 3 4 5 x -3 -2 -1 0 1 2 3 y -3 -2 -1 0 1 2 3 Df = R Feladat: 1. Ábrázoljuk ugyanabban a koordinátarendszerben a következő függvényeket! yx y  2x y  5x xR y  3x Ez ugyanazt jelenti, min t : x  x x  2x vagy f (x)  x f(x )  2x x  5x x  3x f(x)  5 x f(x)  3x Mindegyik függvény grafikonja egyenes. Az elsőfokú függvényeket lineáris függvényeknek is nevezik. Megfigyelhető, hogy a függvény bármelyik egész koordinátájú pontjából, ha egyet jobbra lépünk, és annyit fel amennyivel az x szorozva van, akkor a függvény egész koordinátájú pontjába jutunk. Ha az x együtthatója negatív, akkor lefelé kell menni Minél nagyobb az x együtthatója, annál meredekebb az egyenes, ezért az egyenes meredekségének nevezzük. Jele: m 2.

Ábrázoljuk ugyanabban a koordinátarendszerben a következő függvényeket! f  x   2x f  x   2x  3 xR f  x   2x  5 –3 –2 –1 0 1 2 3 f(x) = 2x –6 –4 –2 0 2 4 6 f(x) = 2x+3 –3 –1 3 5 7 8 x 1 f(x) = 2x– 5 –11 – 9 – 7 – 5 – 3 – 1 1 Ha az f(x) = 2x függvény grafikonját 3-mal feltoljuk, akkor az f(x) = 2x + 3 függvény grafikonjához jutunk. Naná! Ha minden helyen hárommal növeljük az f(x) = 2x függvény értékét, akkor az f(x) = 2x + 3 függvény értékeit kapjuk. f(x) = 2x + 3 ha x = 0  f(0) = 2·0 + 3 = 3 A függvény 3-nál metszi az y tengelyt. f(x) = 2x – 5 ha x = 0  f(0) = 2·0 – 5 = – 5 A függvény – 5-nél metszi az y tengelyt. Az elsőfokú függvények általános alakja: y  mx  b m a meredekség x  0  f(x)  m  0  b  b b az egyenes y tengelymetszete Ábrázoljuk az f  x   2x  5 függvényt! Kapásból is ábrázolhatjuk!

A függvény 5-nél metszi az y tengelyt, és a meredeksége –2. 2 x  4 függ3 vényt! A függvény 4-nél metszi az y 2 tengelyt, és a meredeksége . 3 3. Ábrázoljuk az f  x   Mit lehet tenni, ha a meredekség tört? 2 -t nem tudunk felfelé menni. 3 De ha az y tengely metszettől hármat megyünk jobbra és kettőt fel, az ugyanaz, mintha egyet megyünk jobbra és kétharmadot fel. (Hasonló háromszögek!) Ha a függvény y tengely metszete sem egész szám, akkor keresni kell a függvénynek egy egész koordinátájú pontját (ha van) és abból kell kiindulni a meredekséggel! A továbbiakban tudnod kell, hogy mi az elsőfokú függvény meredeksége, és az y tengely metszete. Összefoglalás: Az elsőfokú függvények általános alakja: y  mx  b , ahol m a meredekség és b az egyenes y tengelymetszete. Ha a függvény bármelyik egész koordinátájú pontjából, egyet jobbra lépünk, és a meredekséggel fel (ha m>0), akkor a függvény

egész koordinátájú pontjába jutunk. Ha a meredekség negatív, akkor lefelé kell menni Az elsőfokú függvényeket úgy ábrázoljuk, hogy az y tengelymetszetéből indulunk a meredekséggel (ha a b egész szám). Feladatok: 1. Ábrázolja az f(x) = – 2x és az f(x) = 3x függvényeket! Mennyi a függvény értéke az x = 2 helyen? Melyik helyen (hol?) 12 a függvény értéke? 1 4 3 2. Ábrázolja az f(x)  x , x  x , y   x függvényeket! 2 3 2 3. Ábrázolja az x  2x  3 , f(x) = 3x – 6 függvényeket! Mennyi a függvény értéke az x = 2 helyen? Melyik helyen (hol?) 12 a függvény értéke? 4. Ábrázolja az f  x   3 x  4, 2 és az f  x    1 x  2 függvényeket! 4 5. Adott a függvény grafikonja Adja meg a függvények képletét! Megoldások: 1. Ábrázolja az f(x) = – 2x és az f(x) = 3x függvényeket! Mennyi a függvény értéke az x = 2 helyen? f(x) = – 2x  f(2) = – 2·2 = – 4 Melyik helyen

(hol?) 12 a függvény értéke? f(x) = – 2x 2. Ábrázolja az f(x)  1 x, 2 x 3 x, 2 y  12 = – 2x  x=–6 4 x függvényeket! 3 f(x) = 3x – 6 függvényeket! Mennyi a függvények értéke az x = 3. Ábrázolja az x  2x  3 , 2 helyen? Melyik helyen (hol?) 12 a függvények értéke? Mennyi a függvények értéke az x = 2 helyen? f(x) = 3x – 6  f(2) = 3·2 – 6 = 0 f(x) = – 2x + 3  f(2) = – 2·2 + 3 = – 1 Melyik helyen (hol?) 12 a függvények értéke? f(x) = 3x – 6  12 = 3x – 6 x = 6 f(x) = – 2x + 3  12 = – 2·x+ 3  x = – 4,5 4. Ábrázolja az f  x   3 x4, 2 és az f  x    1 x  2 függvényeket! 4 5. Adott a függvény grafikonja Adja meg a függvények képletét! A fekete grafikonnal megadott függvény képlete: y = x + 4 A kék grafikonnal megadott függvény képlete: y = 3x + 1 A lila grafikonnal megadott függvény 1 képlete: y  x  2 4 A zöld

grafikonnal megadott függ2 vény képlete: y   x  3 5