Fizika | Középiskola » Illy Judit - Impulzus momentum

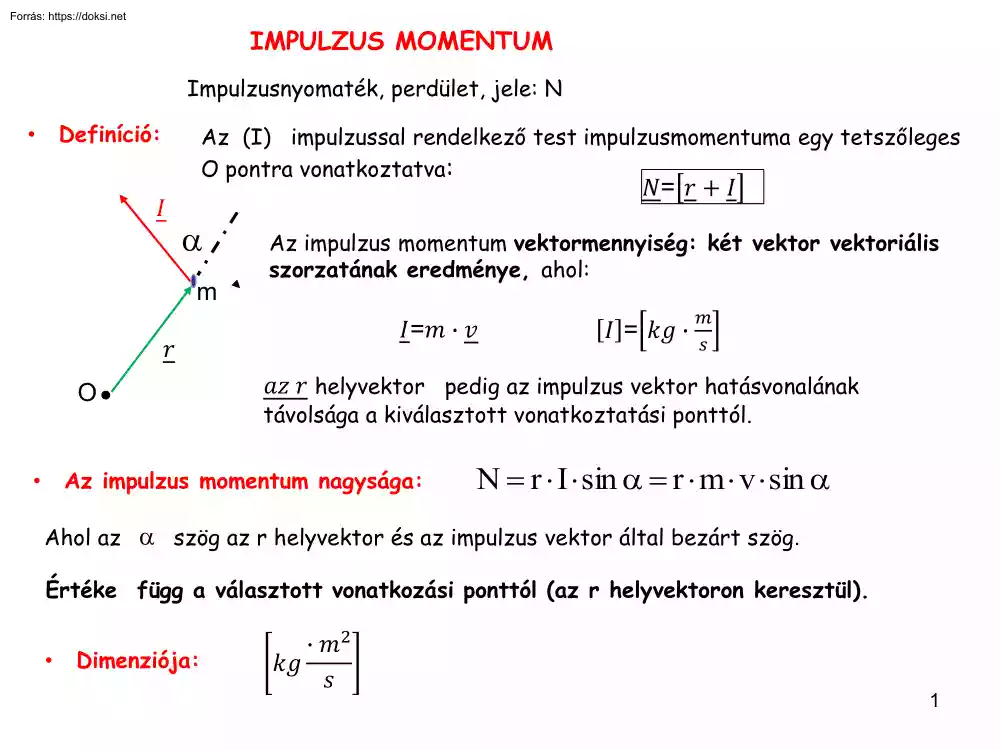
IMPULZUS MOMENTUM Impulzusnyomaték, perdület, jele: N Definíció: • Az (I) impulzussal rendelkező test impulzusmomentuma egy tetszőleges O pontra vonatkoztatva: � �= � + �  m Az impulzus momentum vektormennyiség: két vektor vektoriális szorzatának eredménye, ahol: �=� ∙ � � O � � �� � helyvektor pedig az impulzus vektor hatásvonalának távolsága a kiválasztott vonatkoztatási ponttól. Az impulzus momentum nagysága: • � = �� ∙ N  r  I  sin   r  m  v  sin  Ahol az  szög az r helyvektor és az impulzus vektor által bezárt szög. Értéke függ a választott vonatkozási ponttól (az r helyvektoron keresztül). • Dimenziója: ∙ �2 �� � 1 •Iránya: A helyvektor és az impulzusvektor által kifeszített síkra a jobb kéz szabály szerint merőleges. A sorrend számít! �= � + � � �  � �= � × � A sorrend felcserélésével az � vektor

iránya 180 fokkal megváltozik. Az impulzus momentum idő szerinti megváltozása  dN d    rI dt dt   Idő szerinti változás: deriválás idő szerint ahol I mv    A deriválást a szorzat deriválási szabályának megfelelően elvégezzük: �� �� = �� × �� + � × �� Ahol: �� =� �� és � �∙� �� � �∙� �� =� N. II Törvény 2 Ezek behelyettesítésével: �� �� =� ×�∙� +� ×� De az első tag nulla, mivel v és I párhuzamos vektorok, így a vektorszorzat értéke nulla: �×�∙� =0 így a végeredmény: �� �� =� ×� A helyvektor és az erő vektoriális szorzata a forgatónyomaték, M A forgatónyomaték definíciója: az erő hatásvonalának helyvektora és az erővektor vektoriális szorzata r F  M    Impulzus momentum tétel a forgatónyomatékkal megfogalmazva: dN  dt M  •Az impulzus

momentum idő szerinti megváltoztatásához forgatónyomaték kell. •Ha a forgatónyomaték nulla, az impulzus momentum irány és nagyság szerint is állandó.3 Impulzus momentum megmaradásának tétele: dN Ha a testre ható erők eredő forgatónyomatéka nulla, akkor a test az impulzusmomentuma állandó. Ha �=0, akkor  dt 0 � = állandó Forgató nyomaték: Definíció: Az F erőnek az O pontra vonatkoztatott forgatónyomatéka: M  r F    Ahol r az O vonatkoztatási pontból az F erő támadáspontjába húzott helyvektor. F  Vektoriális szorzat: •Nagysága:  r  M  r  F  sin   az erő és a helyvektor által bezárt szög •Iránya: jobb kéz szabály szerint a helyvektor és az erővektor által kifeszítette síkra merőleges O •Mértékegysége: M   N  m 4 Forgatónyomaték a középiskolában: M  F k F k - erőkar: az erő hatásvonalának távolsága a

forgástengelytől Az O pontból merőlegest kell bocsátani az erő hatásvonalára: ez lesz az erőkar    r k  r  sin  M  F  k  F  r  sin   � Az erőkar kifejezhető az r helyvektor és az  szög segítségével: k M  r F    Visszakapjuk a forgatónyomaték általános kifejezését. Az irány miatt a vektoriális szorzatban a vektorok sorrendjét meg kell tartani! 5 Impulzus momentum megmaradásának tétele: Ha a testre ható erők forgatónyomatékainak összege nulla, akkor a test impulzus momentuma állandó. Ha M=0, akkor N=állandó Példa: centrális erő: pl: bolygómozgás Centrális erő mindig a két testet összekötő egyenes mentén hat, így mindig párhuzamos lesz a helyvektorral. A gravitációs erő centrális erő. A Naptól a bolygóhoz húzott helyvektor minden pillanatban párhuzamos az erővel, és ellentétes irányú. r  Nap F bolygó  M0 mert  De r 0 Fg

 0  r ll F   A gravitációs erő és a helyvektor mindig párhuzamos egymással, így vektoriális szorzatuk nulla. 6 Az impulzus momentum ilyen esetben tehát irány és nagyság szerint is állandó. • N Nagysága: N  m  r  v  sin   állandó Az impulzus momentum nagysága a Napközeli és a Naptávoli pontban egyenlő:   90 m  rp  vp  m  ra  va Kepler II. tv: a területi sebesség állandó A bolygók a Nap közelében felgyorsulnak: rp � vp 0 v p  va � va ra Kepler II. törvényének dinamikai igazolása •N Iránya: a keringés síkjára végig merőleges. A sebesség mindig ugyanabban a síkban marad, a bolygók síkmozgást végeznek. A mozgás megtartja a síkját. Ugyanez történik biciklizés közben is Ha a forgó kerekekre nem hat forgatónyomaték, a biciklikerék is megtartja forgási síkját, is kell a kormányt tartani. 7