Matematika | Analízis » Függvények deriválása, megoldással

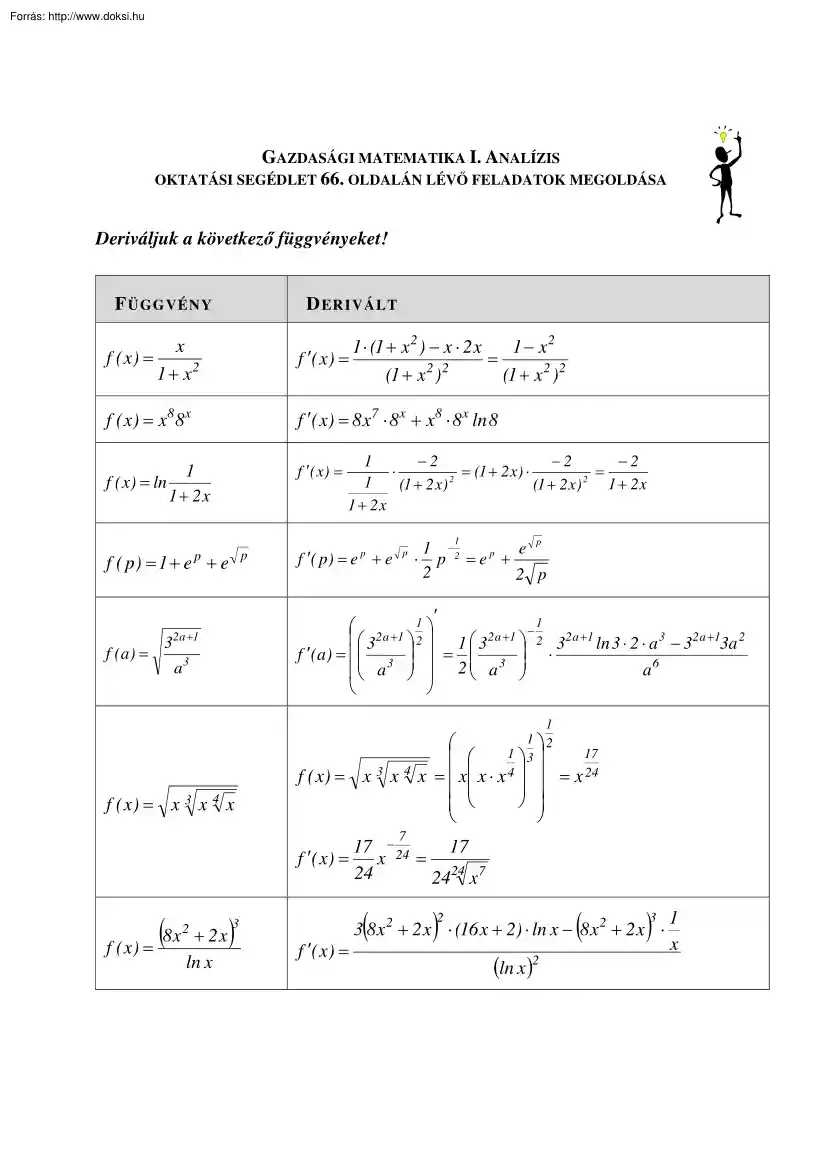
GAZDASÁGI MATEMATIKA I. ANALÍZIS OKTATÁSI SEGÉDLET 66. OLDALÁN LÉVŐ FELADATOK MEGOLDÁSA Deriváljuk a következő függvényeket! F ÜGGVÉNY D ERIVÁLT x f ( x) = 1 + x2 1 ⋅ (1 + x 2 ) − x ⋅ 2 x 1 − x2 f ′( x) = = (1 + x 2 ) 2 (1 + x 2 ) 2 f ( x ) = x8 8 x f ′( x) = 8 x 7 ⋅ 8 x + x8 ⋅ 8 x ln 8 1 f ( x) = ln 1 + 2x f ′( x) = f ( p) = 1 + e + e p p f (a ) = −2 −2 1 −2 ⋅ = (1 + 2 x) ⋅ = 2 2 1 1 + 2x (1 + 2 x) (1 + 2 x ) 1 + 2x f ′( p) = e + e p 1 p 1 − e p ⋅ p 2 =ep + 2 2 p ′ 1  2 a +1 1  − a + 2 1  3  2  2 32 a +1 ln 3 ⋅ 2 ⋅ a 3 − 32 a +13a 2 13 f ′(a) =   3   =  3  ⋅ a6  a   2  a    32 a+1 a3 1 f ( x) = x 3 x 4 f ( x) = x 3 x 4 x 1 2  1 3  17     4  = x 24 x =x x⋅x          7 17 − 24 17 f ′( x) = x = 24 2424 x 7 (8x f ( x) = + 2x ln x 2 ) 3 f ′( x) = ( )

( 2 ) 3 3 8 x 2 + 2 x ⋅ (16 x + 2) ⋅ ln x − 8 x 2 + 2 x ⋅ (ln x )2 1 x 4 ln 3 p ⋅ ln 4 p f ( p) = p 3 f ′( p ) = ( f ( x) = e x x 2 + 3 x5 f (a ) = 2 +a a a ) 1 ⋅ p − ln 4 p ⋅ 1 4 ln 3 p − ln 4 p p = p2 p2 ( 3 ) ( ) ( a a 2 2 x ( f ( x) = e x x 2 − 2 x + 2 1 + ex x + 2x f ( x) = 3e − x 2 ln x 2 f ( x) = x +6x−4 2 1 1 − 2 f ( x) = x − = x 3 − 2x 2 x 3 f ( x) = 3 ) ) 1 −2 2 ln 2 + 2a a − 2 + a a 2 ′ f (a) = a 2 f ( x) = 3 x 2 − ( 3 f ′( x) = e x 3x 2 ⋅ x 2 + 3x 5 + e x ⋅ 2 x + 15 x 4 2 1 3 − 2 − 2 1 f ′( x) = x 3 + x 2 = 3 + 3 3 x x3 ) ( e ( f ′( x) = ) f ′( x) = e x x 2 − 2 x + 2 + e x (2 x − 2 ) = e x x 2 x 3 ) x + 2 x − (1 + e x )(1 3 x − 2 3 + 2 x ln 2) ( 3 f ′( x) = 3e − x 1 f ′( x) = x 2 2 +6x−4 x + 2x 2 ⋅ (− 2 x + 6 ) ⋅ 2 x ⋅ x − ln x 2 ⋅ 1 x2 ) = 2 − ln x 2 x2