Medical knowledge | Biophysics » Hipotézis vizsgálat

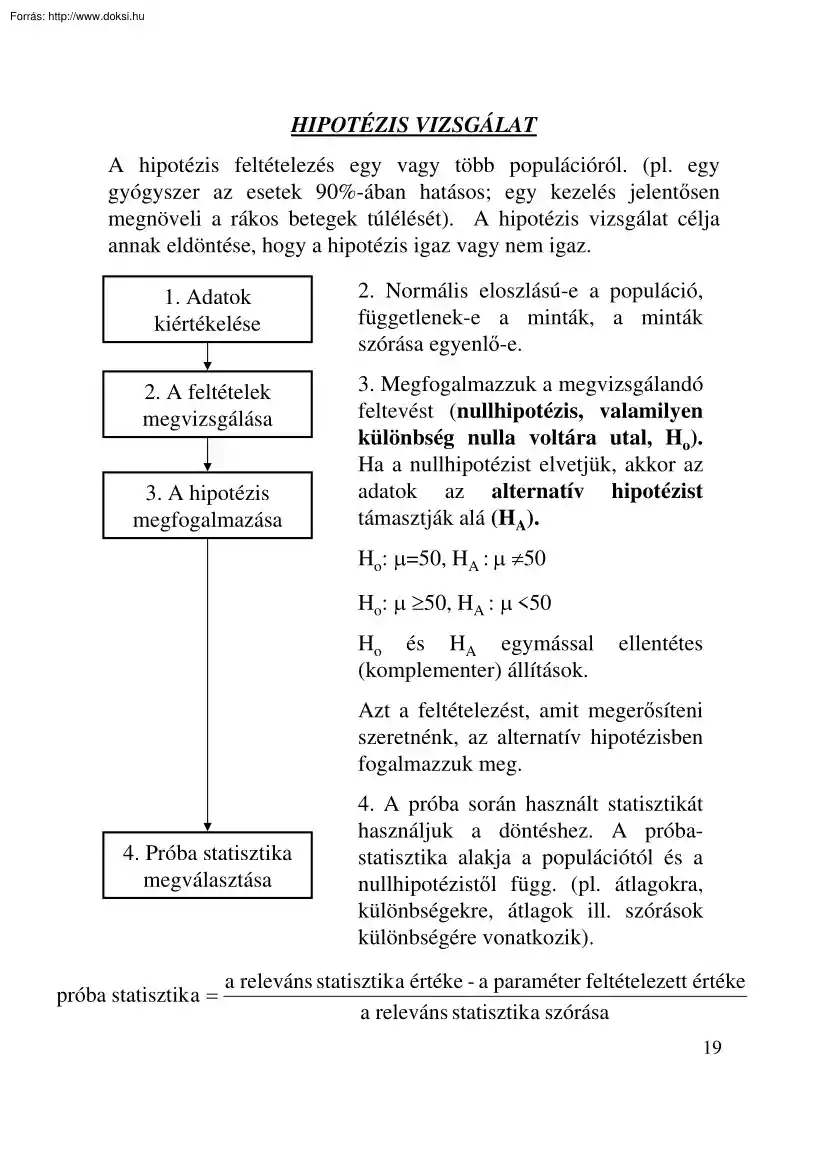
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat célja annak eldöntése, hogy a hipotézis igaz vagy nem igaz. 1. Adatok kiértékelése 2. Normális eloszlású-e a populáció, függetlenek-e a minták, a minták szórása egyenlő-e. 2. A feltételek megvizsgálása 3. Megfogalmazzuk a megvizsgálandó feltevést (nullhipotézis, valamilyen különbség nulla voltára utal, Ho). Ha a nullhipotézist elvetjük, akkor az adatok az alternatív hipotézist támasztják alá (HA). 3. A hipotézis megfogalmazása Ho: μ=50, HA : μ ≠50 Ho: μ ≥50, HA : μ <50 Ho és HA egymással (komplementer) állítások. ellentétes Azt a feltételezést, amit megerősíteni szeretnénk, az alternatív hipotézisben fogalmazzuk meg. 4. Próba statisztika megválasztása próba statisztik a = 4. A próba során

használt statisztikát használjuk a döntéshez. A próbastatisztika alakja a populációtól és a nullhipotézistől függ. (pl átlagokra, különbségekre, átlagok ill. szórások különbségére vonatkozik). a releváns statisztik a értéke - a paraméter feltételezett értéke a releváns statisztik a szórása 19 6. A statisztika lehetséges értékeit két csoportba osztjuk: az elfogadási és az elutasítási tartományokra. Az elutasítási tartomány értékei kisebb valószínűséggel következnek be, ha a nullhipotézis igaz. A döntési szabály azt mondja ki, hogy a nullhipotézist el kell vetnünk, ha a statisztika értéke az elutasítási tartományba esik, és el kell fogadni, ha az elfogadási tartományba esik. 5. Meghatározni a használt próbastatisztika eloszlását 6. Megfogalmazni a döntés kritériumát 0.45 Kétoldali próba 0.4 A próba statisztika eloszlása, ha a nullhipotézis igaz sűrűségfüggvény 0.35 0.3 0.25 0.2 0.15 kis

valószínűséggel előforduló értékek, ha a nullhipotézis igaz 0.1 0.05 0 a próba statisztika értékei elutasítási tart. elfogadási tartomány elutasítási tart. Kétoldali próbák: az elutasítási tartomány az eloszlás két széle közt van szétosztva. A statisztikának mind a túl nagy, mind a túl kis értékei esetén elvetjük a nullhipozézist. Ho: μ=20, HA: μ ≠20 20 0.45 0.4 A próbastatisztika eloszlása, ha a nullhipotézis teljesül One-sided test Egyoldali próba sűrűségfüggvény 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0 a próbastatisztika értékei elfogadási tartomány elutasítási tart. Egyoldali próba: az egész elutasítási tartomány az eloszlás valamelyik széléhez tartozik. Ho: μ≤20, HA: μ >20 Szignifikancia szint (α): megadja az eloszlás sűrűségfüggvényének görbe alatti területét az elutasítási tartományban. Mivel az igaz nullhipotézis elutasításának valószínűsége éppen α, α értékét kicsinek

választjuk, hogy ez a valószínűség csekély legyen. Az igaz nullhipotézis elutasítása az ún. elsőfajú hiba (valószínűsége α). A hamis nullhipotézis megtartása az ún. másodfajú hiba 21 7. A próbastatisztika kiszámítása 8. Statisztikai döntés 8. Ha a statisztika kiszámított értéke az elutasítási tartományban van, a nullhipotézist elutasítjuk. A statisztika táblázata megadja az elfogadási és az elutasítási tartomány határán lévő számértéket (kritikus érték). 9. Ha Ho-t elutasítjuk, alternatív hipotézis igaz. Elutasítjuk Ho -t akkor az Következtetés: HA igaz Nem utasítjuk el Ho -t Következtetés: H0 lehet, hogy igaz A hipotézis vizsgálat nem jelenti a nullhipotézis igaz vagy hamis voltának egyértelmű bizonyítását. Csupán azt jelzi, hogy a rendelkezésre álló adatok alátámasztják-e a hipotézist. 22 Hipotézis vizsgálat: egyetlen populáció átlaga 1. Ismert szórás esetén Példa: A kutatók egy

enzim szintjének átlagos értékére kíváncsiak. Levonhatják-e azt következtetést egy 10 elemű minta alapján, melynek átlagértéke 22, szórásnégyzete pedig 45, hogy a populáció várható értéke eltér 25-től (0.05 szignifikancia szint mellett)? Feltételezés: a minta normális eloszlású populációból származik. Hipotézis: Ho: μ=25, HA: μ≠25 Próba statisztika: u= x−μ σ/ n A próba statisztika eloszlása: standard normális (μ=0, σ=1). Döntési szabály: kétoldali próba (u-nak mind elegendően nagy, mind elegendően kicsiny értékei esetén elvetjük a nullhipotézist). Meg kell keresnünk a standard normális eloszlás legfelső és legalsó 5/2=2.5 %-ának megfelelő kritikus értéket 0.45 sűrűségfüggvény 0.4 a próba statisztika eloszlása a nullhipotézis teljesülése esetén (standard normális eloszlás) kétoldali próba 0.35 0.3 0.25 0.2 7.9 % 0.15 0.1 7.9 % 2.5 % 2.5 % 0.05 0 -1.96 -1.41 0 a próba statisztika

értékei 1.96 23 A próba statisztika értékének kiszámítása az adott minta esetén: u= 22 − 25 = −1.41 45 / 10 Statisztikai döntés: mivel -1.41 az elfogadási tartományban van, nem vetjük el a nullhipotézist. Következtetés: lehetséges, hogy μ értéke egyenlő 25-tel. A próba p értéke annak valószínűsége, hogy Ho teljesülése esetén a próba statisztika értéke legalább olyan szélsőséges (legalább annyira eltér a várható értéktől a megfelelő irányban), mint a megfigyelt érték. A fenti próba p értéke 0.079+0079=0158 Példa 2: A kutatók egy enzim szintjének átlagos értékére kíváncsiak egy sokaságban. Levonhatják-e azt a következtetést egy 10 elemű minta alapján, melynek átlagértéke 22, szórásnégyzete pedig 45, hogy a populáció várható értéke kisebb mint 25 (0.05 szignifikancia szint mellett)? 0.45 0.4 a próba statisztika eloszlása a nullhipotézis teljesülése esetén (standard normális eloszlás)

Egyoldali próba sűrűségfüggvény 0.35 0.3 0.25 0.2 7.9 % 0.15 0.1 5% 0.05 0 -1.96 -1.41 -1.645 0 a próba statisztika értékei 1.96 24 Ho: μ≥25, HA:μ<25 A próba statisztika az előbbivel azonos, de a kritikus érték -1,645. Mivel -1,41>-1,65, nem vetjük el a nullhipotézist. A próba p értéke 0.079 2. A sokaság szórása ismeretlen (ez a gyakoribb eset) Ilyenkor a populáció szórását a minta korrigált empírikus szórásával közelítjük. A próba statisztika: t n −1 = x−μ = Sn / n x−μ ∑ ( x − x) 2 i n(n − 1) Eloszlása ún. Student-féle t eloszlás n-1 szabadsági fokkal Két sokaság átlagának eltérése A mintát normál eloszlású, független, ismeretlen, de egyenlő szórású sokaságokból vesszük Próba statisztika tn+ m−2 = x− y (n − 1) ⋅ S x2 + (m − 1) ⋅ S y2 ⎛ 1 1 ⎞ ⋅⎜ + ⎟ n+m−2 ⎝n m⎠ Mely n+m-2 szabadsági fokú t eloszlást követ. (n és m a minták elemszáma, Sx és Sy a

minták korrigált empirikus szórása. Ezen próba elvégzése előtt a sokaságok szórásának egyenlőségét ellenőrizni kell (F-próbával). 25 Önkontrollos (egymintás) t-próba Az önkontrollos kísérlet célja az, hogy minél több olyan külső tényezőtől megszabaduljunk, ami a mintaelemek értékét befolyásolhatja. Ezért olyan összetartozó értékpárokat hasonlítunk össze, melyek közt különbséget legfőként az alkalmazott kezelés okozhat. Ugyanazon egyedeken végzünk mérést egy bizonyos kezelés előtt és után. Majd nem a két mintát, hanem az összetartozó értékpárok különbségét (d) vetjük alá a vizsgálatnak. A próba statisztika: t= d − μd Sn / n ahol Sn a különbségek alkotta minta szórása és elméleti várható értéke. PÉLDA: 12 egyén koleszterin szintjét vizsgálták meg egy különleges étrenddel együtt alkalmazott edzés előtt és után. Kellően alátámasztják-e az adatok a kezelés hatásosságát? 1 2

3 4 5 6 7 8 9 10 11 12 SZÉRUM KOLESZTERIN kezelés előtt kezelés után 201 200 231 236 221 216 260 233 228 224 237 216 326 296 235 195 240 207 267 247 284 210 201 209 különbség -1 5 -5 -27 -4 -21 -30 -40 -33 -20 -74 8 26 Ho: μd≥0, HA: μd<0 d= Sn = ∑ (d i − d ) 2 n −1 = ∑d n i = ∑ d i2 − nd ( n − 1) t= − 242 = −20.17 12 2 10766 − 12 ⋅ (−20.12) 2 = = 23.13 11 − 20.17 − 0 = −3.02 23.13 / 12 A t kritikus értéke -1.7959 005 szignifikancia szint mellett Mivel -3.02<-17959 (t az elutasítási tartományba esik), elvetjük a nullhipotézist. (Azaz az adatok alátámasztják a feltevést, hogy a koleszterin szint szignifikánsan csökkent.) Két populáció szórásnégyzetének aránya A próba statisztika S x2 F= 2 Sy ún. F eloszlású nx-1 szabadsági fokkal a számlálóban és ny-1 szabadsági fokkal a nevezőben. Kétoldali próba elvégzésekor (pl ha a kétmintás t-próba előtt a szórások egyenlőségét

szeretnénk megvizsgálni), a nagyobbik szórásnégyzetet tesszük a nevezőbe. A VI. és VII táblázat a jegyzet végén csak az 1-nél nagyobb értékeket tartalmazza, és p=2,5% és 1%-ra van megadva. Ezek segítségével így voltaképpen 5, ill. 2% szignifikancia szint melletti kétoldali próbák végezhetők. Egyoldali a próba esetén a megfelelő próba statisztika az Sx2 / Sy2 ha a nullhipotézis σx≤ σy. 27