Please log in to read this in our online viewer!
Please log in to read this in our online viewer!
No comments yet. You can be the first!
Content extract
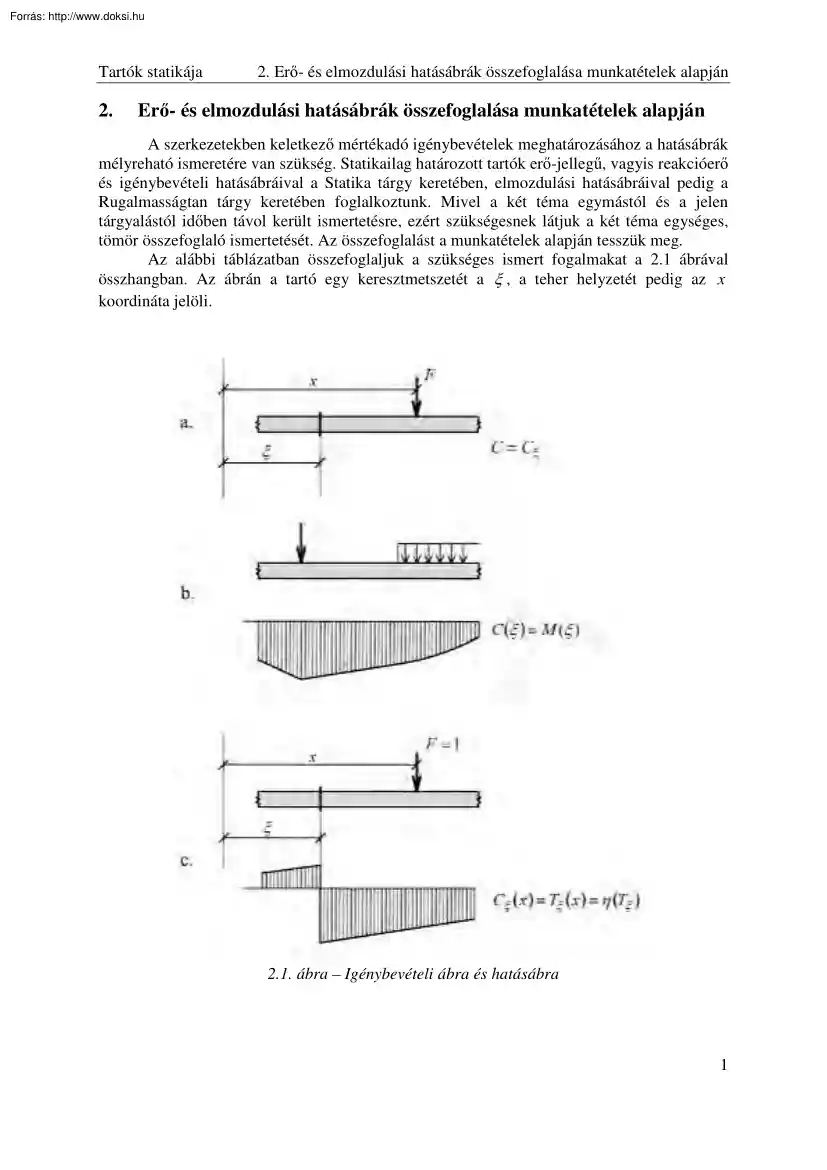
Tartók statikája 2. 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A szerkezetekben keletkez mértékadó igénybevételek meghatározásához a hatásábrák mélyreható ismeretére van szükség. Statikailag határozott tartók er -jelleg&, vagyis reakcióer és igénybevételi hatásábráival a Statika tárgy keretében, elmozdulási hatásábráival pedig a Rugalmasságtan tárgy keretében foglalkoztunk. Mivel a két téma egymástól és a jelen tárgyalástól id ben távol került ismertetésre, ezért szükségesnek látjuk a két téma egységes, tömör összefoglaló ismertetését. Az összefoglalást a munkatételek alapján tesszük meg Az alábbi táblázatban összefoglaljuk a szükséges ismert fogalmakat a 2.1 ábrával összhangban. Az ábrán a tartó egy keresztmetszetét a , a teher helyzetét pedig az x koordináta jelöli. 2.1 ábra –
Igénybevételi ábra és hatásábra 1 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Mechanikai jellemz k ábrái és hatásábrái Fogalom Jelölés Definíció Hatáson minden olyan mérhet mechanikai mennyiséget (reakcióer , igénybevétel, elmozdulás) értünk, amely a tartó egy rögzített keresztmetszetében ( ) a teher helyzetének (x) a függvényében adható meg (2.1a ábra) Az igénybevételi vagy elmozdulási függvény/ábra (C ( )) leírja egy rögzített helyzet (álló) teheregyüttes hatására az adott mechanikai jellemz (C ) változását a keresztmetszet helyzetének ( ) változása függvényében (2.1b ábra) A hatásfüggvény (C ( x)) leírja a tartónak egy rögzített helyzet ( ) Hatás C Igénybevételi és elmozdulási függvény, ábra C( ) Hatásfüggvény C (x) keresztmetszetében keletkez küls vagy bels hatás változását (C ) , a (C ) mozgó egységer$ helyzetének (x) változása
függvényében (2.1c ábra) C (x) Hatásábra (C ) A hatásábra a hatásfüggvény képe. Az er - és elmozdulási hatásfüggvényeket munkatételekb l származtatjuk. Ennek rendjét foglalja össze az alábbi táblázat: Hatásfüggvények származtatása Er -hatásfüggvények Virtuális elmozdulások tétele alapján Elmozdulási hatásfüggvények Virtuális er k tétele alapján 2.1 Statikailag határozott tartók er -hatásfüggvényei a virtuális elmozdulások tétele alapján A virtuális elmozdulások tételét a Rugalmasságtan tárgy keretében tárgyaltuk. A tétel ismertetése az alkalmazásokkal együtt Kaliszky, Kurutzné és Szilágyi Szilárdságtan cím& tankönyvében található [4]. A virtuális elmozdulások tétele szerint egy er$rendszer akkor és csak akkor statikailag lehetséges (egyensúlyi), ha bármely virtuális elmozdulásrendszeren végzett munkája zérus. Er -hatásábrák készítésekor a mozgó egységteher és az általa okozott, vele
egyensúlyban lév küls és bels er k változását vizsgáljuk. A tétel értelmében az egységteher és a következtében fellép küls és bels er k tetsz leges virtuális elmozdulásrendszeren végzett munkájának összege az egységteher minden helyzetében zérus. A virtuális munka felírásához a tartón tetsz leges virtuális elmozdulásrendszert kell felvenni. A virtuális elmozdulásrendszer alapvet tulajdonsága, hogy kompatibilis, azaz 2 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján geometriailag lehetséges, vagyis elemei a geometriai egyenletek által megszabott összefüggésben állnak egymással. Ezt az elmozdulásrendszert úgy kell felvennünk, hogy a vizsgált er hatás feltétlenül munkát tudjon végezni rajta, ugyanakkor elégítse ki a tartón érvényes geometriai kerületi feltételeket. Az egységteher pedig a tartón így létrejöv virtuális elmozdulásrendszeren végez munkát. A kétféle
virtuális munka összegének - mivel az er rendszer az egységteher minden helyzetében egyensúlyban van - zérust kell adnia. Ha a vizsgált er$hatás küls$ jelleg (reakcióer$), akkor virtuális elmozdulást, ha pedig bels$ jelleg (igénybevétel), akkor virtuális alakváltozást (relatív elmozdulást) iktatunk be. Hogy a beiktatandó elmozdulásnak vagy alakváltozásnak helyet csináljunk, a tartót minden esetben át kell alakítani. Virtuális elmozdulás beiktatásához az elmozdulásnak megfelel eredeti kényszer-komponenst el kell távolítani, virtuális alakváltozás beiktatásához pedig az alakváltozási komponens jellegének megfelel en a tartón egy-szabadságfokú bels „átvágást” kell végrehajtani. Ez a beavatkozás a tartó elmozdulási (kinematikai) szabadságfokát minden esetben eggyel növeli, azaz a tartót egy fokkal fellazítja. A virtuális elmozdulás vagy alakváltozás beillesztésekor általános esetben a fellazított tartó mentén
virtuális elmozdulás-alakváltozás-rendszer jön létre. Ha a tartó statikailag határozott volt, akkor a fellazítás következtében egy-szabadságfokú, kényszermozgású láncolattá alakul, amelynek elmozdulását a beiktatott elmozdulás vagy alakváltozás egyértelm&en meghatározza. Virtuális elmozdulás beiktatása esetén a láncolat mentén csak elmozdulások jönnek létre, alakváltozások nem. Virtuális alakváltozás beiktatásakor ugyanez a helyzet, kivéve a beiktatás keresztmetszetét, ahol a beiktatott virtuális alakváltozás szinguláris alakváltozásként van jelen (csak a beiktatás helyén van alakváltozás, máshol nincs). Az egyensúlyban lév tartón a küls és bels virtuális munkaösszeg zérust ad. A virtuális küls$ munka két részb l állhat: a vizsgált küls er hatásnak (reakcióer ) a beiktatott virtuális elmozduláson végzett munkájából, valamint a tartón mozgó egységtehernek a hatásvonalába es virtuális elmozdulásokon
végzett munkájából. A virtuális bels$ munka is két részb l állhat: a vizsgált bels er hatásnak (igénybevétel) a beiktatott virtuális alakváltozáson végzett munkájából, valamint a tartón mozgó egységteherb l keletkez bels er knek (igénybevételek) a virtuális alakváltozás-rendszeren végzett munkájából. Statikailag határozott tartó esetén, amikor a beavatkozás eredményeként kialakult láncolaton nem keletkeznek virtuális alakváltozások, ez az utóbbi bels munka zérus. Mivel a tartószerkezetek terhei tipikusan gravitációs terhek, a tartón mozgó egységteher függ leges er , amely függ leges eltolódásokon végez munkát. Statikailag határozatlan tartók er -hatásfüggvényeinek az el állítása a virtuális elmozdulások tétele alapján a bels virtuális munka kiszámítása miatt nehézkes. Ezért az alábbiakban csak a statikailag határozott tartók esetével foglalkozunk. Ugyanakkor a statikailag határozatlan tartók er
hatásábráival foglalkozó fejezetekben utalni fogunk a virtuális elmozdulások tétele alapján nyerhet megoldásra is. 2.11 Küls er k (reakcióer k) hatásfüggvényei Legyen a tartón mozgó egységer F , helyzetének koordinátája x . Határozzuk meg a C küls reakcióer (C ) hatásfüggvényét! Távolítsuk el a reakcióer nek megfelel kényszerkomponenst, és iktassuk be a helyén a reakcióer vel munka-kompatibilis e virtuális elmozdulást. Ez a terhel egységer hatásvonalában v e ( x) virtuális eltolódást okoz A teljes virtuális munka most csak küls részb l áll, azaz W = Wk = F v e ( x) + C e = 0 . 3 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Figyelembe véve, hogy F = 1 , továbbá, hogy a e virtuális elmozdulás tetsz leges, ezért egységnyinek is felvehet , így a küls er hatásfüggvényére az alábbi kifejezést nyerjük (C ) = v e=1 ( x) = v e= 1 ( x) . Eszerint: Egy küls$ er$
(reakcióer$) hatásfüggvénye a támasz helyén beiktatott, a reakcióer$vel munka-kompatibilis, azzal ellentett irányú egységnyi virtuális elmozdulásból kapott, egységteher-irányú eltolódásfüggvénnyel azonos. Mivel az egységteher a gravitációs terhek esetén függ leges er , és a tartószerkezetek terhei legtöbbször ilyenek, függ leges eltolódási ábráról van szó. A beiktatott egységnyi virtuális elmozdulás pedig abszolút, így kimondhatjuk, hogy: A küls$ reakcióer$ hatásábrája a támasz helyén beiktatott, a reakcióer$vel munkakompatibilis, azzal ellentett irányú egységnyi abszolút elmozdulásból kapott függ$leges eltolódási ábra. Küls reakcióer hatásábrája esetén tehát az egységnyi abszolút elmozdulást az er pozitív irányával ellentétesen kell felvenni, hogy el jelhelyes hatásábrát kapjunk. Példaként határozzuk meg a 2.2 ábrán látható tartón a B reakcióer hatásábráját Mivel a pozitív B reakcióer felfelé
mutat, a vele munka-kompatibilis e = 1 virtuális eltolódást - a támasz eltávolítása után - lefelé vesszük fel. Az eredményként kapott függ leges eltolódási ábra az (B ) hatásábra. 2.2 ábra – Küls$ er$k hatásfüggvényei 4 Tartók statikája 2.12 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Bels er k (igénybevételek) hatásfüggvényei A helyen rögzített keresztmetszethez tartozó (C ) bels er (igénybevételi) hatásfüggvény esetén a keresztmetszetnél a bels er vel (igénybevétellel) munka-kompatibilis virtuális alakváltozást (relatív elmozdulást) iktatunk be, miután az ehhez szükséges egyszabadságfokú bels átvágást végrehajtottuk. A beiktatott virtuális alakváltozás hatására a terhel F er hatásvonalában v (x) virtuális eltolódás keletkezik. A teljes virtuális munka most küls és bels részb l áll, azaz, mivel a bels virtuális munka negatív W = Wk + Wb = F v ( x) C = 0. virtuális
alakváltozás tetsz leges, tehát egységnyinek is felvehet , így a Mivel F = 1 , és a bels er hatásfüggvénye az alábbi formát ölti (C ) = v =1 ( x ) . Eszerint: Egy keresztmetszet bels$ er$ (igénybevételi) hatásfüggvénye a keresztmetszetben beiktatott, a bels$ er$vel munka-kompatibilis egységnyi virtuális alakváltozásból kapott függ$leges eltolódásfüggvénnyel azonos. 2.3 ábra – Bels$ er$k hatásfüggvényei 5 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Mivel a beiktatott szinguláris alakváltozás nem más, mint koncentrált relatív elmozdulás, kimondhatjuk, hogy: Az igénybevételi hatásábra a keresztmetszetben beiktatott, az igénybevétellel munkakompatibilis, azzal egyez$ irányú egységnyi relatív elmozdulásból kapott függ$leges eltolódási ábra. Igénybevételi hatásábra esetén tehát az egységnyi relatív elmozdulást az igénybevétel pozitív irányával megegyez en kell
felvenni, hogy el jelhelyes hatásábrát kapjunk. Példaként határozzuk meg a 2.3 ábrán látható tartó koordinátájú K keresztmetszetének nyomatéki hatásábráját. Ehhez a keresztmetszetnél csuklót iktatunk be, majd létrehozzuk a pozitív nyomatékkal egyez irányú = 1 relatív elfordulást. Az így létrejött függ leges eltolódási ábra a keresett ( M K ) hatásábra. Az ábrán feltüntettük a gerendának a keresztmetszetben elképzelt differenciálisan kicsiny hosszúságú szakaszát, a Szilárdságtanból jól ismert rúdelemet, amelynek mindkét véglapjára felrajzoltuk a pozitív keresztmetszeti nyomatékot. Látható, hogy a beiktatott relatív elfordulás el jele a nyomatékéval megegyezik. Az egyes igénybevételi fajtáknak megfelel en beiktatandó egy-szabadságfokú bels kapcsolatokat és relatív elmozdulásokat az alábbi táblázatban foglaljuk össze a 2.4 ábrával összhangban, ahol ugyancsak a keresztmetszetnél kimetszett rúdelemre
rajzoltuk fel a pozitív igénybevételeket. 2.4 ábra - A relatív elmozdulásnak megfelel$ egy-szabadságfokú bels$ kapcsolat 6 Tartók statikája Hatásfüggvény, hatásábra 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Jele A beiktatott alakváltozás (relatív elmozdulás) Az egy-szabadságfokú bels átvágást biztosító kapcsolat Normáler Nyíróer Hajlítónyomaték Rúder 2.13 kizárólag tengelyirányú relatív eltolódást engedélyez görg (TK ) kizárólag tengelyre mer leges relatív eltolódást engedélyez görg kizárólag relatív elfordulást (M K ) engedélyez csukló ( S ij ) kizárólag tengelyirányú relatív eltolódást engedélyez görg (N K ) egységnyi koncentrált relatív eltolódás a rúd tengelye (érint je) irányában egységnyi koncentrált relatív eltolódás a rúd tengelyére (érint jére) mer legesen egységnyi koncentrált relatív elfordulás (érint k törése), forgáspont a rúd
tengelyében egységnyi koncentrált relatív eltolódás a rúd tengelye irányában Egy-szabadságfokú láncolatok eltolódási ábrái Amint láttuk, a statikailag határozott síkbeli tartók er -hatásábrái egy-szabadságfokú síkbeli láncolatok függ leges eltolódási ábráira vezetnek. A síkbeli láncolatok több merev tárcsából állnak, amelyeket síkbeli kényszerekkel, legtöbbször csuklókkal kapcsolunk egymáshoz és az aljzathoz. Egyszer& feladatok esetén felírhatjuk a függ leges eltolódási ábra függvényét is, amely a hatásfüggvénnyel azonos. Minthogy a hatásábra poligon, a keresztmetszetnél szingularitással, a vonatkozó hatásfüggvény nem folytonos, azaz ún. nemsima függvény Az ilyen függvényeket szakaszonként külön-külön függvényekkel adják meg, a függvényt alkotó rész-függvények halmazát kapcsos jellel rendelve egymáshoz. Az alkalmazási gyakorlatban azonban a kézi számításokhoz közvetlenül a hatásábrát
állítják el , míg magára a hatásfüggvényre a számítógépes algoritmusok készítésénél van szükség. A láncolatok függ leges eltolódási ábráit számítással és szerkesztéssel határozhatjuk meg. A számítással történ megoldás a Statika és a Szilárdságtan tantárgyakban tanult módon történik [3,4]. Az elmozdulásokra vonatkozó alapösszefüggések szerint Valamely keresztmetszet (j) abszolút elmozdulásai ( keresztmetszet (i) abszolút elmozdulásainak ( ( ij , u kl ) az együttesével. i j , e j ) egyenérték ek egy megel$z$ , ei ) és a köztük lév$ relatív elmozdulásoknak A zárt vonal relatív elmozdulásai együtt ( ij , u kl ) egyenérték ek nullával. E két összefüggés alapján a vizsgált láncolat tetszés szerinti elemének, pontjainak elmozdulásai kiszámíthatók, és maga az eltolódási ábra is felrajzolható. Ha a láncolatok függ leges eltolódási ábráit szerkesztéssel kívánjuk meghatározni, akkor a fenti
összefüggéseket szerkesztéshez szükséges formában kell megfogalmaznunk. A szerkesztés a láncolati pólusok közötti összefüggéseken alapszik. A keresztmetszet abszolút elmozdulásának ( i , ei ) elfordulás-középpontját abszolút pólusnak (i), relatív elmozdulásának 7 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján ( jk , u jk ) elfordulás-középpontját relatív pólusnak (j,k) nevezzük. Az elmozdulásoknál megszokott módon az abszolút pólust egy jellel (bet&vel, számmal), a relatív pólust két jellel jelöljük, a vonatkozó tárcsák jelére utalva. A jeleket kerek zárójelbe tesszük A pólusokra vonatkozó összefüggések az elmozdulásokra vonatkozó összefüggésekkel összhangban: Az i-edik tárcsa (i ) abszolút pólusa és a j-edik tárcsa ( j ) abszolút pólusa a két tárcsa (i, j ) relatív pólusával egy egyenesen van. Az (i, j ) , ( j , k ) és (i, k ) relatív pólusok egy
egyenesen vannak. Az els állítás jelölése: (i ), ( j ) (i, j ) vagy (i ), (i, j ) ( j) vagy ( j ), (i, j ) (i ) A második állítással egyenérték& jelölések: (i, j ), ( j , k ) (i, k ) , vagy (i, j ), (i, k ) ( j , k ) , vagy (i, k ), ( j , k ) (i, j ) E két összefüggés segítségével a láncolat elmozdulási ábrája megszerkeszthet , azaz a szerkesztéshez szükséges hiányzó abszolút vagy relatív pólusok megkereshet k. A szerkesztés során a hatásábra jellemz ordinátái geometriai úton meghatározhatók. További, a fentiekb l következ állítások: - Az abszolút pólus nem mozdul el, ezért képe az eltolódási ábra zérustengelyén van. - Az a tárcsa, amelyen egynél több abszolút pólust lehet kimutatni, nem mozdul el, képe a zérustengellyel esik egybe. - Ha egy tárcsa abszolút pólusa a végtelenben van, a tárcsa önmagával párhuzamosan tolódik el. - Ha két tárcsa relatív pólusa a végtelenben van, a két tárcsa
egymással párhuzamosan mozdul el. - Abszolút eltolódás pólusa az eltolódásra mer leges egyenesen van. - Relatív eltolódás pólusa az eltolódásra mer legesen a végtelenben van. Az egy-szabadságfokú láncolatok abszolút és relatív pólusai közötti összefüggéseket illusztrálja a 2.5a, b, c és d ábra 8 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.5 ábra - Egy-szabadságfokú láncolatok abszolút és relatív pólusai közötti összefüggések 2.14 Mintapéldák: Er -hatásábrák a virtuális elmozdulások tétele alapján Amint láttuk, a hatásábra-készítés lényegében a beiktatott egységnyi abszolút vagy relatív elmozdulás hatására a láncolat függ leges eltolódási ábrájának elkészítéséb l áll. Ez számítással és szerkesztéssel történhet. Láncolatok elmozdulásainak számítással történ meghatározását a Statikában és a Szilárdságtanban részletesen
ismertettük. Az alábbiakban a számítással és szerkesztéssel történ megoldás lépéseit foglaljuk össze. Statikailag határozott tartók küls és bels er -jelleg& hatásábráinak virtuális elmozdulások tétele (vagy a gyakorlatban elterjedt kifejezéssel: kinematikai módszer) alapján történ meghatározása lépéseit számítás és szerkesztés alapján az alábbi táblázatokban foglaljuk össze. Az er -hatásábra-készítés lépései számítással 1. 2. 3. A meghatározandó küls , vagy bels er nek megfelel en átalakítjuk a tartót: vagy eltávolítjuk a reakcióer nek megfelel küls kényszerkomponenst, vagy beiktatjuk az igénybevételnek megfelel egy-szabadságfokú bels átvágást biztosító kapcsolatot. Ezáltal kialakítottuk az egy-szabadságfokú láncolatot. Az így kialakult láncolaton kinematikai teherként beiktatjuk az egységnyi abszolút elmozdulást a pozitív küls er vel ellentétesen, illetve az egységnyi relatív elmozdulást a
pozitív igénybevétellel megegyez en. A láncolatok elmozdulásaira vonatkozó egyenérték&ségek alapján kiszámítjuk a függ leges eltolódási ábra – a keresett hatásábra – jellemz ordinátáit. Ha szükséges, az ordináták segítségével felírhatjuk a hatásfüggvény szakaszonként lineáris függvényét is. 9 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Az er -hatásábra-készítés lépései szerkesztéssel 1. 2. 3. 4. 5. 6. 7. A meghatározandó küls , vagy bels er nek megfelel en átalakítjuk a tartót: vagy eltávolítjuk a reakcióer nek megfelel küls kényszerkomponenst, vagy beiktatjuk az igénybevételnek megfelel egy-szabadságfokú bels átvágást biztosító kapcsolatot. Ezáltal kialakítottuk az egy-szabadságfokú láncolatot. Az így kialakult láncolaton beszámozzuk a tárcsákat, és a hozzájuk tartozó – közvetlenül megállapítható – abszolút és relatív
pólusokat. Szabadon felvesszük egy olyan tárcsa kimozdult képét, amelyik a kívánt egységnyi elmozduláshoz kapcsolódik. A kimozdított tárcsához viszonyítva beillesztjük az egységnyi abszolút elmozdulást a pozitív küls er vel ellentétesen, illetve az egységnyi relatív elmozdulást a pozitív igénybevétellel megegyez en. Megszerkesztjük a láncolat, pontosabban a „pályát” alkotó tárcsák elmozdult képét, (azon tárcsákét, amelyeket a mozgó egységer útja során érint). Ehhez megkeressük a szükséges abszolút és relatív pólusokat, felhasználva a pólusokra vonatkozó összefüggéseket. Végül megszerkesztjük a zérustengelyt, amely az abszolút pólusok képének geometriai helye. A hatásábrát a pályát alkotó tárcsák képe és a zérustengely közötti tartomány alkotja. Az így el állított hatásábrának számszer&en meghatározzuk a szükséges jellemz ordinátáit. M-2.11 Kéttámaszú konzolos tartó igénybevételi
és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a kéttámaszú tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.11a ábra 10 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A küls és bels virtuális munkák összege zérus (a bels mindig negatív): F v( x) M K ( x) K = 0, ahol F a tartón mozgó, x helyzet& egységer , v(x) a K keresztmetszetben beiktatott K virtuális relatív elfordulásból keletkez függ leges eltolódási ábra, és M K ( x) a keresztmetszeti nyomaték F er helyzetét l függ en változó értéke, maga a hatásábra: M K ( x) = ( M K ) . Mivel F = 1, és K = 1 , így a keresztmetszet nyomatéki hatásábrája a keresztmetszeti nyomatékkal munka-kompatibilis egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos: ( M K ) =
v( x) . A nyomatéknak megfelel en tehát átalakítjuk a tartót: csuklót teszünk be a keresztmetszetnél, hogy a relatív elfordulást beiktathassuk. Ekkor a tartó egy-szabadságfokú láncolattá alakul Beszámozzuk a tárcsákat, és a közvetlenül megállapítható abszolút és relatív pólusokat. A fix támasz csuklója a II. jel& tárcsa (2) abszolút pólusa, a két tárcsát összekapcsoló csukló pedig az (1,2) relatív pólus. Az (1) abszolút pólus a görg s megtámasztásnál keletkez abszolút eltolódásra mer leges egyenesen helyezkedik el, ugyanakkor a (2) abszolút és az (1,2) relatív pólusok által meghatározott egyenesen is rajta kell lennie, azaz (2), (1,2) (1) , így az (1) abszolút pólus a két egyenes metszéspontjában, a görg s megtámasztási pontban van. Ezután szabadon felvesszük például az I. tárcsa képét, azaz elmozdult helyzetét, amelyre levetítjük az (1,2) relatív pólust. Itt beiktatjuk a K = 12 = 1 relatív elfordulást
úgy, hogy a II. tárcsát a pozitív nyomatéknak megfelel el jellel fordítjuk el az I tárcsához képest Mivel az II. tárcsa a bal oldali tartórész, a balról számított igénybevételek el jelszabálya szerint a pozitív nyomatéknak megfelel en ez az óra járásával megegyez elfordítást jelenti. (Ha a II. tárcsa képét vesszük fel kiindulásként, és ehhez képest az I tárcsát fordítjuk el, amely a jobb oldali tartórésznek felel meg, akkor a jobb oldali el jelszabály szerint az óra járásával ellentétes elfordítást kell alkalmaznunk. Ez természetesen ugyanazt az alakzatot eredményezi.) Ekkor tehát megkapjuk a tárcsák elmozdult alakját, már csak a nullvonalat kell megszerkesztenünk. Az eltolódási ábra nullvonala a helyben maradó, el nem mozduló pontok geometriai helye. Az abszolút pólusok nem mozdulnak el, így azokat levetítve, majd összekötve, megkapjuk a nullvonalat és egyben a függ leges eltolódási ábrát, azaz az ( M K )
hatásábrát. A szerkesztéssel kapott ábra ordinátáit a 12 = 1 elfordulásból számíthatjuk, hiszen távolságra a támasz alatt ugyancsak nagyságú eltolódás keletkezik, amelyb l már attól bármely ordináta számítható. b) Határozzuk meg a kéttámaszú tartó K keresztmetszetének (TK ) hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer A küls és bels virtuális munkák összege most (a bels mindig negatív): F v( x) TK ( x) u K = 0 , ahol v(x) most a K keresztmetszetben beiktatott u K virtuális relatív eltolódásból származó függ leges eltolódási ábra. Mivel F = 1, u K = 1 és TK ( x) = (TK ) , így a keresztmetszet nyíróer hatásábrája a keresztmetszeti nyíróer vel munka-kompatibilis egységnyi relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos: (TK ) = v( x) . 11 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.11b ábra
Most tehát a nyíróer nek megfelel en alakítjuk át a tartót: görg s kapcsolatot teszünk be a keresztmetszetnél úgy, hogy a nyírásirányú relatív eltolódást beiktathassuk. Ekkor a tartó ugyancsak egy-szabadságfokú láncolattá alakul. Beszámozzuk a tárcsákat, és a közvetlenül megállapítható abszolút és relatív pólusokat. A fix támasz csuklója most is a II jel& tárcsa (2) abszolút pólusa, azonban az (1,2) relatív pólus most a u K eltolódásra mer legesen a végtelenben van, mivel a két tárcsa párhuzamosan mozdul el. Az (1) abszolút pólus most is a görg s támasz támasztási felületére mer leges egyenesen helyezkedik el, ugyanakkor a (2) abszolút és az (1,2) relatív pólusok által meghatározott egyenesen is rajta kell lennie, vagyis (2), (1,2) (1) , így az (1) abszolút pólus a két egyenes metszéspontjában, a görg s megtámasztási pontban van. Vegyük fel az I. tárcsa képét, azaz elmozdult helyzetét Ez után beiktatjuk a
u K = u12 = 1 relatív eltolódást úgy, hogy a bal oldali II. tárcsát a pozitív nyíróer nek megfelel el jellel párhuzamosan eltoljuk az I. tárcsához képest Mivel a II tárcsa a bal oldali tartórész, az igénybevételek el jelszabálya szerint ez a II. tárcsa felfelé való eltolását jelenti (Ha a II. tárcsa képét vesszük fel kiindulásként, akkor a jobb oldali I tárcsát a jobboldali el jelszabály szerint lefelé kell eltolni, amely természetesen ugyanazt az alakzatot eredményezi.) Ezáltal megkapjuk a tárcsák elmozdult alakját, majd az abszolút pólusokat levetítve és összekötve megkapjuk a nullvonalat, és egyben a függ leges eltolódási ábrát, azaz az (TK ) hatásábrát. A szerkesztéssel kapott ábra bármely ordinátája egyszer&en számítható c) Határozzuk meg a kéttámaszú tartó A támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! ( A) A virtuális munkaösszeg most
csak küls munkákból áll: F v( x) + A( x) u A = 0 , ahol v(x) a függ leges eltolódási ábra az A támasznál beiktatott u A virtuális abszolút eltolódásból. Mivel F = 1, u A = 1 és A( x) = ( A) , így az A támaszer hatásábrája a támaszer vel munka-kompatibilis egységnyi abszolút eltolódásból rajzolt függ leges eltolódási ábra ellentettjével azonos: ( A) = v( x) , 12 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.11c ábra ezért a pozitív reakcióer vel ellentétesen, lefelé mutatóan kell beiktatni a virtuális eltolódást. Most a reakcióer nek megfelel en alakítjuk át a tartót: eltávolítjuk a megtámasztást, hogy az abszolút eltolódást beiktathassuk. Ekkor a tartó olyan egy-szabadságfokú láncolattá alakul, amely mindössze egyetlen tárcsából áll. Az (1) abszolút pólus most is a görg s megtámasztás megtámasztási felületére mer leges egyenesen helyezkedik el, ezt
levetítve a kimozdított tárcsa képére megkapjuk a tárcsa helyben maradó, nullvonalon lév pontját. A nullvonal másik pontját az A támasznál beiktatott egységnyi eltolódás kezd pontja jelöli ki. Ezáltal megkapjuk a függ leges eltolódási ábrát, azaz az ( A) hatásábrát. A szerkesztéssel kapott ábra bármely ordinátája egyszer&en számítható. M-2.12 Gerber-tartó igénybevételi és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a Gerber-tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! A keresztmetszet nyomatéki hatásábrája a keresztmetszeti nyomatékkal munkakompatibilis egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél csuklót teszünk be, hogy a relatív elfordulást beiktathassuk. Ekkor a tartó három tárcsából álló egy-szabadságfokú
láncolattá alakul. Beszámozzuk a tárcsákat A fix támasz csuklója a középs , II. jel& tárcsa (2) abszolút pólusát adja meg, míg a két széls tárcsához csatlakozó csukló az (1,2) és a (2,3) relatív pólusokat jelöli ki. Az (1) és (3) abszolút pólusok a megfelel görg s megtámasztások megtámasztási felületére mer leges egyenesen helyezkednek el. Ugyanakkor az (1) pólusnak a (2) abszolút és az (1,2) relatív, a (3) pólusnak pedig a (2) abszolút és a (2,3) relatív pólusok által meghatározott egyenesen is rajta kell lennie, azaz (2), (1,2) (1) , illetve (2), (2,3) (3) . Így az (1) és (3) abszolút pólusok a megfelel görg s megtámasztási pontokban vannak. 13 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.12a ábra Szabadon felvesszük vagy a II., vagy a III tárcsa képét, majd beiktatjuk a = K 23 = 1 virtuális relatív elfordulást a pozitív nyomatéknak megfelel en. Ezután
levetítjük a (2) és (3) abszolút pólusokat a II. és III tárcsák képére, ezáltal megkapjuk a nullvonalat. A nullvonalra levetítve az (1) abszolút pólust, az I tárcsa egy pontját kapjuk, míg a másik pontját a II. tárcsa képére levetített (1,2) relatív pólus adja E két pontot összekötve megkapjuk az I. tárcsa képét is, és ezáltal el állítottuk az ( M K ) hatásábrát A hatásábra ordinátáit a 23 = 1 elfordulásból kiindulva számíthatjuk. b) Határozzuk meg a Gerber-tartó egy másik keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (TK ) nyíróer 2.12b ábra A keresztmetszet nyíróer hatásábráját a keresztmetszeti nyíróer vel munkakompatibilis egységnyi relatív eltolódásból rajzolt függ leges eltolódási ábra adja. Most tehát a nyíróer nek megfelel görg s kapcsolatot teszünk be a keresztmetszetnél. Ekkor a tartó ugyancsak három tárcsából álló egy-szabadságfokú
láncolattá alakul. Beszámozzuk a tárcsákat. Mivel a III tárcsa két pontjában is meg van támasztva, nem mozdul el, vagyis minden pontja abszolút pólus. Ezért a III tárcsa tetsz legesen felvett képe a nullvonallal esik 14 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján egybe. A u K = u 23 = 1 virtuális relatív eltolódás beiktatásakor a jobbra lév II tárcsát lefelé kell párhuzamosan eltolni. Az I tárcsa képét a II tárcsa képére levetített (1,2) relatív, és a nullvonalra levetített (1) abszolút pólusok összekötése adja meg. Ezáltal megkaptuk a függ leges eltolódási ábrát, azaz az (TK ) hatásábrát. A hatásábra bármely ordinátája egyszer&en számítható. c) Határozzuk meg a Gerber-tartó befüggesztett tartórészén lév keresztmetszetének (TK ) nyíróer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.12c ábra A keresztmetszetnél beiktatott
görg s kapcsolatot a tartót ugyancsak három tárcsából álló egy-szabadságfokú láncolattá alakítja. A III tárcsa most is mozdulatlan, mivel két pontjában is meg van támasztva, tehát minden pontja abszolút pólus. A tárcsa tetsz legesen felvett képe tehát a nullvonal, amelyen most a (2,3) relatív pólus is rajta van. A u K = u12 = 1 virtuális relatív eltolódás beiktatásakor az I. és II tárcsákat egymástól egységnyire párhuzamosan eltoljuk, majd az (1) abszolút és a (2,3) relatív pólusok nullvonalra való levetítésével megkapjuk a hatásábrát. A hatásábra bármely ordinátája ezután egyszer&en számítható. d) Határozzuk meg a Gerber-tartó B támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (B ) 2.12d ábra 15 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A B támaszer hatásábrája a támaszer vel ellentett,
azzal munka-kompatibilis egységnyi abszolút eltolódásból rajzolt függ leges eltolódási ábrával azonos. A reakcióer nek megfelel en eltávolítjuk a megtámasztást, ekkor a tartó két tárcsából álló egy-szabadságfokú láncolattá alakul. Az (1) és (2) abszolút pólusok a görg s megtámasztás megtámasztási felületére mer leges egyenesen helyezkednek el. Vegyük fel a II tárcsa képét a pozitív reakcióer vel ellentétesen, a lefelé mutatóan beiktatott e B = e B = 1 virtuális eltolódásnak megfelel en. A (2) pólust levetítve a tárcsa képére, megkapjuk a tárcsa helyben maradó, nullvonalon lév pontját. A nullvonal másik pontját a B támasznál beiktatott egységnyi eltolódás kezd pontja jelöli ki. Megrajzolva a nullvonalat, és levetítve rá az (1) pólust, az I tárcsa egyik pontját kapjuk meg. A másik pontját az (1,2) relatív pólus II tárcsára levetített képe adja. Így megkapjuk a függ leges eltolódási ábrát, azaz az (B )
hatásábrát Az ordináták az e B = 1 eltolódás alapján számíthatók. M-2.13 Háromcsuklós tartó igénybevételi hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a háromcsuklós tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13a ábra A keresztmetszet nyomatéki hatásábrája a keresztmetszetben beiktatott egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott csukló hatására a tartó három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói az I., illetve a III tárcsa megfelel abszolút pólusát adják meg, míg az eredeti és a beiktatott közbens csuklók az (1,2) és a (2,3) relatív pólusokat jelölik ki. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a levetített (2,3) relatív forgáspontban a pozitív
nyomatéknak megfelel en elfordítjuk hozzá képest a másik tárcsát K = 23 = 1 értékkel. A nullvonalhoz a (3) abszolút póluson kívül a (2)-re is szükségünk van. Ezt az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések által meghatározott egyenesek metszéspontja adja meg. Levetítve az abszolút pólusokat a 16 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét a nullvonalon lév (1) abszolút és a II. tárcsára levetített (1,2) abszolút pólus összekötése adja meg, és ezáltal el állítottuk az ( M K ) hatásábrát. A hatásábra ordinátáit a 23 = 1 elfordulásból kiindulva számíthatjuk. b) Határozzuk meg a háromcsuklós tartó K keresztmetszetének (TK ) nyíróer hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13b ábra A keresztmetszet nyíróer hatásábrája a
keresztmetszetben beiktatott egységnyi nyírásirányú relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó ugyancsak három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói most is az I, illetve a III tárcsa megfelel abszolút pólusát adják meg, míg a közbens csukló alkotja az (1,2) relatív pólust, azonban a (2,3) relatív pólus a beiktatott görg s kapcsolat által meghatározott elmozdulási irányra mer legesen a végtelenben van, mivel a II. és a III tárcsa csak egymással párhuzamosan mozdulhat el. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, a görg s kapcsolat mentén eltolva ket egymáshoz képest a pozitív nyíróer nek megfelel en u K = u 23 = 1 értékkel. Mivel azonban nekünk az alkalmazott munkatétel értelmében a függ leges eltolódások ábrájára van szükségünk, az ábrán a tárcsákat u Ky
= u 23, y = 2 / 2 mértékben toljuk el egymáshoz képest függ legesen. A nullvonalhoz most is szükségünk van a (2) pólusra, amelyet most is az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések által meghatározott egyenesek metszéspontja határoz meg. Levetítve az abszolút pólusokat a megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét most is a nullvonalon lév (1) abszolút és a II. tárcsa képére levetített (1,2) relatív pólus összekötése adja meg, és ezáltal megkapjuk az (TK ) hatásábrát. Ezután kiszámítjuk a hatásábra ordinátáit. 17 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján c) Határozzuk meg a háromcsuklós tartó K keresztmetszetének ( N K ) normáler hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13c ábra A keresztmetszet normáler hatásábrája a keresztmetszetben beiktatott egységnyi tengelyirányú
relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó most is három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói most is az I, illetve a III tárcsa megfelel abszolút pólusát adják meg, míg a közbens csukló alkotja az (1,2) relatív pólust, de most a (2,3) relatív pólus a beiktatott görg s kapcsolatnál a rúd tengelyére mer legesen a végtelenben van, mivel a II. és a III tárcsa tengelyirányban mozdul el egymással párhuzamosan. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén tengelyirányban eltoljuk ket egymáshoz képest a pozitív normáler nek megfelel en u K = u 23 = 1 értékkel. Az alkalmazott munkatétel értelmében a függ leges eltolódások ábrájára van szükségünk, ezért az ábrán a tárcsákat u Ky = u 23, y = 2 / 2 mértékben toljuk el egymáshoz képest függ
legesen. A nullvonalhoz most is szükségünk van a (2) pólusra, amely azonban az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések szerint most a végtelenben van, ami azt jelenti, hogy a II. tárcsa a nullvonallal párhuzamos kell legyen Mivel azonban a III. tárcsa képére levetített (3) abszolút pólusnak a nullvonalon kell lennie, és a III. tárcsa a II tárcsával párhuzamos, következésképpen a III tárcsa maga a nullvonal Így a levetített (1) pólus is rajta van, amelyb l a II. tárcsára levetített (1,2) relatív pólus segítségével az I. tárcsa képét, és így az ( N K ) hatásábrát is megkapjuk Ezután kiszámítjuk a hatásábra ordinátáit. 18 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.14 Rácsos tartó rúder hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján Határozzuk meg az alsópályás rácsos tartó jelölt három rúder szerkesztéssel!
hatásábráját 2.14a ábra a) Határozzuk meg az alsópályás rácsos tartó ( S1 ) rúder hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.14b ábra Ehhez átvágjuk a rudat, és a rúd átvágott végei között egységnyi pozitív relatív eltolódást hozunk létre, majd ebb l meghatározzuk a tartón végigmen egységer pályájának, az alsó pályának a függ leges eltolódási ábráját, amely a keresett hatásábrát adja. Az átvágás a rácsos tartót két merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A II tárcsa (2) abszolút pólusa a fix támasz csuklóközéppontja, az (1,2) relatív pólus a két tárcsát összeköt csuklóban van. Az (1) abszolút pólus a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van, de mivel (2), (1,2) (1) , így a görg s támasz csuklóközéppontjában van. Az átvágott rúd két vége között úgy tudjuk legegyszer&bben beiktatni az egységnyi
pozitív relatív eltolódást, ha az (1,2) relatív elfordulás-középpontban az I. és a II tárcsát elfordítjuk egymáshoz képest olymódon, hogy a rúdban éppen a u = u1 = 1 pozitív eltolódás (nyúlás) keletkezzék. Ehhez a relatív elfordulásnak éppen 12 = u1 / 4 = 1 / 4 nagyságúnak kell 19 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján lennie. Vegyük fel tetsz legesen például az I (vagy a II) tárcsa képét, és fordítsuk el hozzá képest a másik tárcsát a 12 = 1 / 4 értékkel úgy, hogy a rúdban nyúlást okozzon. Ezután levetítjük a tárcsákra az abszolút pólusaikat, és berajzoljuk a nullvonalat. Ezáltal megkaptuk a hatásábrát. b) Határozzuk meg az (S 2 ) elmozdulások tétele alapján! rúder hatásábrát is szerkesztéssel, a virtuális 2.14c ábra A ferde rácsrúd átvágása a rácsos tartót négy merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A IV
tárcsa (4) abszolút pólusát a fix támasz csuklóközéppontja adja, míg az (1) abszolút pólus a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2), (1,3), (2,4) és (3,4) relatív pólusokat. Mivel az alsó pálya mentén (2,4), (1,2) (1,4) , ugyanott (4), (1,4) (1) , így az (1) abszolút pólus a görg s támasz csuklóközéppontjában van. Most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be az átvágott rúd két vége között az egységnyi pozitív relatív eltolódást: vagy az (1,2), vagy a (3,4) pólusban. A szükséges relatív elfordulásnak 12 = 34 = u 2 / k = 1 / k nagyságúnak kell lennie, ahol k = 3 / 2 az (1,2) vagy (3,4) pólusok mer leges távolsága az átvágott rúdtól. Mivel alsópályás tartóról van szó, vegyük fel tetsz legesen az I. tárcsa képét, és fordítsuk el hozzá képest a II. tárcsát a 12 = 2 / 3 értékkel úgy,
hogy a rúdban nyúlást okozzon A nullvonal meghatározásához szükségünk van a (2) abszolút pólusra is. A (4), (2,4) (2) és az (1), (1,2) (2) összefüggésekb l megtudjuk, hogy a (2) abszolút pólus az alsó öv vonalán helyezkedik el valahol. Hogy pontosan hol, azt a (3) abszolút pólus segítségével tudhatjuk meg. A (3) pólus helyét a (4), (3,4) (3) és az (1), (1,3) (3) összefüggésekb l kapjuk meg Az (1,2), (1,3) (2,3) és a (2,4), (3,4) (2,3) összefüggésekb l megtudjuk, hogy a (2,3) relatív pólus függ legesen a végtelenben van, ami arra utal, hogy a II. és a III tárcsa párhuzamosan mozdul el. Ugyanakkor most már a (3), (2,3) (2) összefüggés kimetszi a (3) pólus függ legesében a (2) pólus keresett helyét az alsó övön. Ezután levetítjük az I és II tárcsákra az abszolút pólusaikat, és berajzoljuk a nullvonalat. A IV tárcsa hiányzó képét a (4) és (2,4) pólusok levetítéséb l kapjuk meg. Ezáltal megkaptuk az alsópályás
tartó keresett 20 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján rúder hatásábráját. Fels pályás esetben ugyanezt a hatásábrát kapjuk, mivel a II és a III tárcsa képe megegyezik. c) Határozzuk meg az ( S 3 ) rúder elmozdulások tétele alapján! hatásábrát is szerkesztéssel, a virtuális 2.14d ábra A tartó szimmetriatengelyében lév oszlop átvágása révén a rácsos tartó most is négy merev tárcsából álló egy-szabadságfokú láncolattá alakul. A IV tárcsa (4) abszolút pólusát a fix támasz csuklóközéppontja adja. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2), (1,4), (2,3) és (3,4) relatív pólusokat. Az (1) abszolút pólus most is a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van, de most a (4), (1,4) (1) összefüggésb l feljebb, a tartó felett helyezkedik el. Az átvágott rúd két vége között az egységnyi pozitív relatív
eltolódást most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be: vagy az (1,2), vagy a (3,4) pólusban. A szükséges relatív elfordulásnak most 12 = 34 = u3 / 3 = 1 / 3 nagyságúnak kell lennie. Vegyük fel tetsz legesen az I tárcsa képét, és fordítsuk el hozzá képest a II tárcsát a 12 = 1 / 3 értékkel úgy, hogy a rúdban nyúlást okozzon. A nullvonal meghatározásához szükségünk van a (2) abszolút pólusra is. A (4), (3,4) (3) és a (3), (2,3) (2) összefüggésekb l megtudjuk, hogy a (2) abszolút pólus az alsó öv vonalán helyezkedik el. Pontos helyét az (1), (1,2) (2) összefüggésb l kapjuk meg, amely szerint egybeesik az (1,2) relatív pólussal. Ez azt jelenti, hogy az I tárcsa képén az (1) és a (2) abszolút pólus egyaránt rajta van, tehát az I. tárcsa képe a nullvonal A (4), (3,4) (3) , (1,4), (3,4) (1,3) és az (1), (1,3) (3) állításokból megkapjuk, hogy a (3) pólus egybeesik a (3,4) pólussal, tehát a
IV. tárcsa képe is a nullvonalon van A (23) és a (3,4) pólusok levetítésével megkapjuk a III tárcsa képét, és ezzel a keresett hatásábrát is. Látható, hogy alsópályás esetben a hatásábra a pálya vonalának, azaz az I., II, III és IV tárcsák elmozdulási alakzatából áll Fels pályás esetben azonban csak az I. és II tárcsa elmozdulási vonala kell, amely a nullvonalat alkotja Valóban, fels pályás esetben a vizsgált rúd vakrúd. 21 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.15 Vonórudas tartó igénybevételi hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján (TK ) a) Határozzuk meg a vonórudas tartó K keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer 2.15a ábra A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó négy tárcsából álló egy-szabadságfokú láncolattá alakul. A
fix támasz csuklója a III tárcsa (3) abszolút pólusát adja meg, míg a közbens csuklók alkotják az (1,2), (1,4) és (3,4) relatív pólusokat. A (2,3) relatív pólus a beiktatott görg s kapcsolat által meghatározott elmozdulási irányra mer legesen a végtelenben van. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén eltoljuk ket egymáshoz képest a pozitív nyíróer nek megfelel en u K = u 23 = 1 értékkel. A függ leges eltolódási ábrában ez u 23, y = cos vetületként jelenik meg, ahol a vizsgált tartószakasz vízszintessel bezárt szöge. A nullvonalhoz szükségünk van a (2) pólusra, amelyet a (3), (2,3) (2) és az (1), (1,2) (2) összefüggések által meghatározott egyenesek metszéspontja határoz meg. Ehhez azonban el z leg az (1) pólus helyét meg kell határoznunk a görg s megtámasztás függ legesében. Ezt a (3,4), (1,4) (1,3) és az (1,2), (2,3) (1,3) , majd a (3), (1,3) (1) metszéspontok
adják meg. Levetítve a (2) és (3) abszolút pólusokat a megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét a nullvonalon lév (1) és a II. tárcsa képére levetített (1,2) pólus összekötése adja meg, így megkapjuk az (TK ) hatásábrát. 22 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján b) Határozzuk meg a vonórudas tartó K keresztmetszetének ( N K ) normáler hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.15b ábra A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó most is négy tárcsából álló egy-szabadságfokú láncolattá alakul, most azonban a (2,3) relatív pólus a beiktatott görg s kapcsolatnál a rúd tengelyére mer legesen van a végtelenben. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén tengelyirányban eltoljuk ket egymáshoz képest a pozitív
normáler nek megfelel en u K = u 23 = 1 értékkel, ami a függ leges eltolódási ábrában u 23, y = sin értékben jelenik meg. A nullvonalhoz most is szükségünk van a (2) pólusra, amelyet az alábbi összefüggések alapján szerkeszthetünk meg: (1,4), (3,4) (1,3) és (1,2), (2,3) (1,3) , majd (3), (1,3) (1) , végül (1), (1,2) (2) és (3), (2,3) (2) . A (2) és (3) abszolút pólusok levetítésével megkapjuk a nullvonalat, majd az (1) és (1,2) pólusok levetítésével az I. tárcsa képét. Ezzel elkészült a keresett ( N K ) hatásábra c) Határozzuk meg a vonórúdban keletkez er virtuális elmozdulások tétele alapján! (S ) hatásábráját is szerkesztéssel, a A vonórúd átvágásával a tartó most is négy tárcsából álló egy-szabadságfokú láncolattá alakul, most azonban a (3,4) relatív pólus a vonórúd tengelyére mer legesen van a végtelenben. 23 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek
alapján 2.15c ábra A vonórúdban beiktatásra kerül egységnyi pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük az I vagy a II. tárcsa kimozdult alakját, és elfordítjuk egymáshoz képest ket 12 = 1 / h szöggel úgy, hogy a vonórúdban egységnyi nyúlás keletkezzen. Az (1) és (2) abszolút pólusok levetítésével megrajzoljuk a nullvonalat, és ezzel kész a keresett (S ) hatásábra. M-2.16 Rácsos konzol rúder hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján Határozzuk meg a fels pályás rácsos konzol jelölt rúder hatásábráit szerkesztéssel! a) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S1 ) hatásábráját szerkesztéssel, a virtuális Az ( S1 ) hatásábrához a rúd átvágása a rácsos konzolt két merev tárcsából álló egyszabadságfokú láncolattá alakítja át. A II tárcsa mereven kapcsolódik a
falhoz, ezért nem mozdul el, tehát képe a nullvonal. Az (1) abszolút pólus az (1,2) relatív pólussal egybeesik A rúdban beiktatásra kerül egységnyi pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük a II tárcsa képét, azaz a nullvonalat, és az (1,2) pólusban elfordítjuk az I. tárcsát 12 = 4 / 3b szöggel úgy, hogy a rúdban egységnyi nyúlás keletkezzen. Ezzel kész a keresett ( S1 ) hatásábra 24 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.16a ábra b) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S 2 ) hatásábráját szerkesztéssel, a virtuális 2.16b ábra Az ( S 2 ) hatásábrához a rúd átvágása a rácsos konzolt ugyancsak két merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A II tárcsa most is mereven kapcsolódik a falhoz, nem mozdul el, tehát képe
a nullvonal. Az (1) abszolút pólus az (1,2) relatív pólussal egybeesik. A rúdban beiktatásra kerül egységnyik pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük a II tárcsa 25 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján képét, azaz a nullvonalat, és az (1,2) pólusban elfordítjuk az I. tárcsát 12 = 1 / k szöggel úgy, hogy a rúdban egységnyi nyúlás keletkezzen. Ezzel kész a keresett ( S1 ) hatásábra c) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S 3 ) hatásábráját szerkesztéssel, a virtuális 2.16c ábra Az ( S 3 ) hatásábrához a rúd átvágása a rácsos konzolt négy merev tárcsából álló egyszabadságfokú láncolattá alakítja át. Most a IV tárcsa kapcsolódik mereven a falhoz, tehát képe a nullvonal. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2),
(1,3), (2,4) és (3,4) relatív pólusokat. Most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be az átvágott rúd két vége között az egységnyi pozitív relatív eltolódást: vagy az (1,3), vagy a (2,4) pólusban. Vegyük fel tetsz legesen az IV tárcsa képét, vagyis a nullvonalat, és fordítsuk el hozzá képest a II. tárcsát a 12 = 1 / k értékkel úgy, hogy a rúdban nyúlást okozzon. A hiányzó I tárcsa képét az (1,2) és (1,4) pólusok levetítésével szerkesztjük meg Az (1,4) pólust az (1,2), (2,4) (1,4) és az (1,3), (3,4) (1,4) összefüggésekb l a konzolvégen kapjuk meg, és a IV. tárcsa képére, a nullvonalra vetítjük le Ezáltal megkaptuk a keresett rúder hatásábrát. 26 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.17 Befogott Gerber-tartó igénybevételi és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján (TK )
a) Határozzuk meg a Gerber-tartó jelölt keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer 2.17a ábra A nyíróer nek megfelel görg s kapcsolat révén a tartó három tárcsából álló egyszabadságfokú láncolattá alakul. Mivel az I tárcsa mereven befogott, így nem mozdul el, minden pontja abszolút pólus. Ezért az I tárcsa képe a nullvonal, és az (1,2) relatív pólus egyben a (2) abszolút pólus is. A II és III tárcsát párhuzamosan eltoljuk egymáshoz képest egységnyivel, majd levetítjük a (2) és (3) pólusokat, és berajzoljuk a nullvonalat. Ezáltal megkaptuk a keresett hatásábrát. b) Határozzuk meg a Gerber-tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.17b ábra 27 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A keresztmetszetnél csuklót
teszünk be, ekkor a tartó ismét három tárcsából álló egyszabadságfokú láncolattá alakul, ahol a mozdulatlan befogott I. tárcsa képe ismét nullvonal Szabadon felvesszük vagy a II., vagy a III tárcsa képét, majd beiktatjuk a 23 = 1 relatív elfordulást a nyomatéki el jelszabály szerint pozitív el jellel. Ezután levetítjük a (2), illetve (3) abszolút pólusokat a megfelel tárcsák képére, és berajzoljuk a nullvonalat. Ezzel el állítottuk az ( M K ) hatásábrát. c) Határozzuk meg a Gerber-tartó A támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (A) 2.17c ábra A reakcióer nek megfelel en eltávolítjuk a megtámasztást, hogy az abszolút eltolódást beiktathassuk. Ekkor a tartó két tárcsából álló egy-szabadságfokú láncolattá alakul, ahol ismét az I. tárcsa képe a nullvonal Ehhez képest vesszük fel a II tárcsa képét úgy, hogy a pozitív reakcióer vel
ellentétesen, lefelé mutató egységnyi eltolódás keletkezzen a támsz helyén. Így megkapjuk az (A) hatásábrát. d) Határozzuk meg a Gerber-tartó befogott tartórészén lév keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.17d ábra 28 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A keresztmetszetnél csuklót teszünk be, ekkor a tartó ismét három tárcsából álló egyszabadságfokú láncolattá alakul, ahol a mozdulatlan befogott I. tárcsa képe ismét a nullvonal, és az (1,2) relatív pólus egyben a (2) abszolút pólus is. E pontban forgatjuk el a II tárcsát az I.-hez képest egységnyi szöggel, majd a III tárcsa képét a (2,3) és (3) pólusok levetítése útján kapjuk meg. Ezzel el állítottuk az ( M K ) hatásábrát 2.2 Statikailag határozott tartók elmozdulási hatásfüggvényei a virtuális er k tétele
alapján A virtuális er k tételét a Rugalmasságtan tárgy keretében tárgyaltuk. A tétel ismertetése az alkalmazásokkal együtt a Szilárdságtan tankönyvben [4] található. A virtuális er$k tétele szerint egy elmozdulásrendszer akkor és csak akkor geometriailag lehetséges (kompatibilis), ha bármely virtuális er$rendszeren végzett (kiegészít$) munkája zérus. Elmozdulási hatásábrák készítésekor a mozgó egységer és az általa okozott, kompatibilis elmozdulás- és alakváltozás-rendszer változását vizsgáljuk. A tétel értelmében az egységer következtében fellép elmozdulások és alakváltozások tetsz leges virtuális er rendszeren végzett kiegészít munkájának összege az egységer minden helyzetében zérus. A virtuális kiegészít munka felírásához a tartón tetsz leges virtuális er rendszert kell felvenni. A virtuális er rendszer alapvet tulajdonsága, hogy egyensúlyi, azaz statikailag lehetséges, vagyis elemei a statikai
egyenletek által megszabott összefüggésben állnak egymással. Ezt az er rendszert tehát úgy kell felvennünk, hogy a vizsgált elmozdulási hatáson feltétlenül munkát tudjon végezni, ugyanakkor elégítse ki a tartón érvényes egyensúlyi feltételeket, amelyek a tartó virtuális igénybevételeihez vezetnek. Ezek a virtuális igénybevételek pedig az egységer b l származó valódi alakváltozásokon (relatív elmozdulásokon) végeznek kiegészít munkát. A kétféle virtuális kiegészít munka összegének – mivel az elmozdulások és alakváltozások kompatibilisek – zérust kell adnia. A virtuális er k tételének ezen felírása alapján megkapjuk a vizsgált elmozdulásnak a mozgó egységer egy adott helyzetéhez tartozó értékét. Ahhoz, hogy a mozgó egységer minden helyzetéhez megkapjuk a vizsgált elmozdulás értékét, azaz az elmozdulás hatásfüggvényét, a virtuális er k tételének két speciális alakját, Betti és Maxwell ún.
felcserélhet ségi tételét kell alkalmaznunk. 2.21 Betti és Maxwell felcserélhet ségi tételei Betti tételének megértéséhez tekintsük az 2.6 ábrán látható rugalmas anyagú, kis elmozdulást végz tartót, amelyre külön a (P), majd külön a (Q) er rendszer m&ködik. Mindkét teherhez meghatározzuk az igénybevételeket és az elmozdulásokat is. A 26a és b ábrán a függ leges eltolódások ábráit t&ntettük fel. 29 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.6 ábra – Betti és Maxwell felcserélhet$ségi tétele Alkalmazzuk kétféleképpen a virtuális er k tételét: el ször a (P), majd a (Q) er rendszert tekintve virtuálisnak, míg a másikat, és az abból származó elmozdulásokat és alakváltozásokat valódinak. A (P) er rendszert tekintve virtuálisnak, a tétel a ~ ~ ~ ~ ~ W = Wk + Wb = Wk , P ,Q + Wb, P ,Q = 0 alakot ölti, míg a (Q) er rendszert tekintve virtuálisnak, a
tétel ~ ~ ~ ~ ~ W = Wk + Wb = Wk ,Q, P + Wb,Q, P = 0 alakját kapjuk, ahol az indexek sorrendjében a munka küls , illetve bels jellege, a munkát végz dinám (illetve a munkavégzés helye), végül a munkában részt vev elmozdulást okozó ~ ~ dinám jut kifejezésre. A Wb, P ,Q és a Wb,Q , P bels kiegészít munkák az integrálkifejezéseikben szerepl igénybevételi függvények szorzatának felcserélhet sége ~ ~ következtében megegyeznek egymással, azaz Wb, P ,Q = Wb,Q , P , következésképpen a küls kiegészít munkák is megegyeznek ~ ~ Wk , P ,Q = Wk ,Q , P . 30 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Eszerint a virtuális (P) er rendszernek a valódi (Q) er rendszerb l származó elmozdulásokon végzett küls kiegészít munkája megegyezik a virtuális (Q) er rendszernek a valódi (P) er rendszerb l származó elmozdulásokon végzett küls kiegészít munkájával. Mivel pedig bármely tényleges
er rendszer virtuálisnak tekinthet , az állítás két valódi er rendszer esetére is igaz. Betti felcserélhet$ségi tétele szerint két dinámrendszer egymás hatására végzett küls$ idegen munkája egyenl$. Írjuk most fel Betti tételét az 2.6c ábrán látható tartóra, amikor a (P), illetve (Q) er rendszer egyetlen P, illetve Q er b l áll: P eP ,Q = Q eQ , P , ahol az els index a hely, a második az ok jelzésére szolgál. Ha mindkét er rendszer egységer kb l áll, azaz P = 1 és Q = 1 , akkor eP ,Q = eQ , P , vagyis a két elmozdulás felcserélhet . Maxwell felcserélhet$ségi tétele szerint két egységdinám által egymás támadáspontján okozott munka-kompatibilis elmozduláskomponensek felcserélhet$k. Más szóval megfogalmazva: két egységdinám esetén az elmozdulás helye és oka felcserélhet . Természetesen Betti és Maxwell tételei érvényesek bármilyen irányú er k és er párok esetén. Elmozdulási hatásábra készítésekor azonban az egyik
er a tartón mozgó – a gravitációs terheket képvisel – függ leges egységer . 2.22 Elmozdulási hatásfüggvények Az elmozdulási hatásfüggvények és hatásábrák készítése munkatételekre, Betti és Maxwell tételeire épül. 2.7 ábra – Elmozdulási hatásábrák 31 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Legyen a tartón mozgó egységer jele F = 1 , helyzetének koordinátája x . Jelölje C a helyen rögzített keresztmetszethez tartozó azon elmozdulást, amelynek (C ) hatásfüggvényét keressük (2.7 ábra) Mivel a C elmozdulást az F er okozza, a „hely-ok” index-sorrend értelmében C = C ,F . Iktassunk be a keresztmetszetben a vizsgált elmozdulással munka-kompatibilis Q = 1 egységdinámot. Ez a terhel F egységer hatásvonalában v F ,Q eltolódást okoz. A végzett küls munkák egyenl sége szerint F v F ,Q = Q C , F . Mivel F = 1 és Q = 1 , C , F = v F ,Q , azaz Maxwell
felcserélhet ségi tétele értelmében: A tartón mozgó egységer$ által okozott keresztmetszeti elmozdulás és a keresztmetszetben beiktatott, az elmozdulással munka-kompatibilis egységdinám által okozott eltolódás az egységer$ hatásvonalában felcserélhet$. A tétel az egységer helyzetét l függetlenül igaz. Mivel tehát az egységer mozog a tartón, és így a Q egységdinám által okozott vF ,Q = vQ=1 ( x) eltolódásfüggvénynek mindig más-más ordinátája fölé kerül, ezért (C ) = vQ=1 ( x) , vagyis a keresett elmozdulási hatásábra megegyezik a beiktatott egységdinám-okozta eltolódási ábrával. Eszerint: Az elmozdulási hatásfüggvény a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú egységdinámból kapott egységteher-irányú eltolódásfüggvénnyel azonos. Mivel a tartón mozgó egységer általában függ leges, az elmozdulási hatásábrakészítés egy függ leges eltolódási ábra
készítésére egyszer&södik. A statikailag határozott és határozatlan tartók elmozdulási hatásfüggvényeinek az el állítása azonos elvek alapján történik, azonban a beiktatott egységdinám hatására készítend függ leges eltolódási ábra meghatározása a statikailag határozatlan tartók esetén a tartó teljes vizsgálatát igényli. Ezért az alábbiakban csak a statikailag határozott tartók esetével foglalkozunk, és a határozatlan tartókra vonatkozó elmozdulási hatásábrákra a statikailag határozatlan tartók megoldásával foglalkozó fejezetekben térünk ki. 2.23 Abszolút és relatív elmozdulások hatásfüggvényei Abszolút eltolódás, illetve elfordulás hatásábráihoz a beiktatott egységdinám az elmozdulás pozitív el jelének megfelel er , illetve er pár. Abszolút elmozdulás hatásábrája a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú egységdinámból kapott függ$leges
eltolódási ábra. 32 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Relatív eltolódás, illetve elfordulás hatásábráihoz a beiktatott egységdinám az elmozdulás pozitív el jelének megfelel kett s er , illetve kett s er pár. A relatív elmozdulás értelmezése szerint a viszonyítási pontok lehetnek távol is egymástól, de egybe is eshetnek. A beiktatott kett s egységdinámoknak a munka-kompatibilitás miatt a viszonyítási pontokat követniük kell. Relatív elmozdulás hatásábrája a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú kett$s egységdinámból kapott függ$leges eltolódási ábra. Elmozdulási hatásábra esetén tehát az egységdinámot az elmozdulás pozitív irányával megegyez en kell felvenni, hogy el jelhelyes hatásábrát kapjunk. Az egyes elmozdulás-fajtáknak megfelel en beiktatandó egységdinámokat az alábbi táblázatban foglaljuk
össze. Hatásfüggvény, hatásábra abszolút eltolódás Jele A beiktatott alakváltozás (relatív elmozdulás) egységnyi koncentrált er az eltolódás irányában relatív eltolódás (eK ) ( K) (u jk ) két ellentett egységnyi koncentrált er az eltolódás irányában relatív elfordulás ( ij ) két ellentett egységnyi koncentrált er pár az elfordulás irányában abszolút elfordulás 2.24 egységnyi koncentrált er pár az elfordulás irányában Mintapéldák: Elmozdulási hatásábrák a virtuális er k tétele alapján Amint láttuk, a hatásábra-készítés a beiktatott egységdinámból származó függ leges eltolódási ábra elkészítéséb l áll. Statikailag határozott és határozatlan tartók elmozdulási hatásábrái egyaránt görbe vonalú ábrák, hiszen a tartó rugalmas vonalával azonosak. Ennek függvényét, az elmozdulási hatásfüggvényt megadni meglehet sen körülményes, hiszen az a rugalmas vonal differenciálegyenletének
megoldását igényelné. Kézi számítások céljára tehát csak a hatásábrát szokták elkészíteni, a függvény felírása nélkül, a függvény meghatározott ordinátáinak a kiszámításával. Az abszolút és relatív eltolódások és elfordulások hatásábráinak számítással történ meghatározása lépéseit az alábbi táblázatban foglaljuk össze. Az elmozdulási hatásábra-számítás lépései 1. 2. Beiktatjuk az elmozdulással munka-kompatibilis egységdinámot a pozitív elmozdulással megegyez en. Meghatározzuk a tartó függ leges eltolódási ábráját, magát a hatásábrát. Ennek módjai lehetnek: a. Eltolódási ábra a Szilárdságtanban tanult nyomatéki teher módszerével: a nyomatéki ábra el állítása után a szükséges támaszelfordulások meghatározása, a közbens (nyomatéki ábra-területekkel arányos) relatív elfordulások meghatározása, az eltolódási ábra el írt ordinátáinak kiszámítása. b. Eltolódási ábra a
Rugalmasságtanban tanult virtuális er k tétele alapján munkatétellel: a hatásábra el írt ordinátáinak közvetlen kiszámítása mindenegyes ordinátára külön alkalmazott munkatétellel. c. Eltolódási ábra kombinált módszerrel: a szükséges támaszelfordulások meghatározása munkatétellel, majd az el írt ordináták számítása a nyomatéki teher módszerével. 33 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.21 Kéttámaszú tartó elmozdulási hatásábrái a) Határozzuk meg a kéttámaszú tartó K keresztmetszetének (eK ) függ leges eltolódási hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . 2.21a ábra A keresztmetszetben beiktatunk egy olyan QK er t, amely a kérdéses eltolódáson munkát tud végezni. A Maxwell-féle felcserélhet ségi tétel értelmében ugyanis ennek a QK er nek a mozgó egységer által okozott, folytonosan változó érték&
keresztmetszeti eltolódáson végzett munkája megegyezik a mozgó egységer nek - bármely helyzetében - a QK er által okozott eltolódásokon végzett munkájával: QK eFK ( x) = F e y ,QK ( x) , ahol eFK ( x) = (eK ) . Mivel QK = 1 és F = 1 , így (eK ) = e y ,QK ( x) , vagyis a keresett eltolódási hatásábra a QK = 1 er hatására keletkez függ leges eltolódási ábrával egyenl . A hatásábra, azaz a függ leges eltolódási ábra görbevonalú. Ezért csak az el re kijelölt keresztmetszetekhez tartozó ordinátáit számítjuk ki, és ennek alapján közelít leg rajzoljuk meg a hatásábrát. A kijelölt ordinátákat valamely tanult módszer szerint számítjuk ki A nyomatéki teher módszere szerint a QK = 1 er b l megrajzolt nyomatéki ábra alapján elegend a B támaszelfordulást kiszámítani, majd a B támasztól kiindulva a keresett eltolódások számíthatók. Az e Ay = 0 feltételb l nagyított értékben B = 2,5 m 2 adódik, amelyb l az (eK ) hatásábra
ordinátáira az alábbi táblázat szerinti értékeket kapjuk: i (eK ) i nagyított [m 3 ] (eK ) i valódi [m / kN ] 0 6,0 10 3 A 1 2,5 6 4,5 2 = 0 6,0 2 2,5 4 2,0 1,333 = 7,33 7,33 10 3 3 2,5 2 0,5 0,667 = 4,67 4,67 10 3 0 B 34 (eK ) i számítása 0 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján b) Határozzuk meg a kéttámaszú tartó K keresztmetszetének hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . ( K ) elfordulási 2.21b ábra A keresztmetszetben beiktatunk egy olyan M K er párt, amely a kérdéses elforduláson munkát tud végezni. A Maxwell-féle felcserélhet ségi tétel értelmében ugyanis ennek az M K er párnak a mozgó egységer által okozott, folytonosan változó érték& keresztmetszeti elforduláson végzett munkája megegyezik a mozgó egységer nek - bármely helyzetében - az M K er pár által okozott eltolódásokon végzett munkájával: M K
FK ( x) = F e y ,M K ( x) , ahol FK ( x) = ( K ) . Mivel QK = 1 és F = 1 , így ( K ) = e y ,M K ( x) , vagyis a keresett elfordulási hatásábra az M K = 1 er pár hatására keletkez függ leges eltolódási ábrával egyenl . A görbevonalú hatásábra ordinátáit az el re kijelölt keresztmetszeteknél számítjuk ki, és ennek alapján rajzoljuk meg a hatásábrát. A kijelölt ordinátákat valamely tanult módszer szerint számítjuk ki. A nyomatéki teher módszere szerint az M K = 1 er párból megrajzolt nyomatéki ábra alapján elegend a B támaszelfordulást kiszámítani, abból kiindulva a keresett eltolódások számíthatók. Az e Ay = 0 feltételb l nagyított értékben B = 1,083 m 2 adódik, amelyb l az ( K ) hatásábra ordinátáira az alábbi táblázat szerinti értékeket kapjuk: i ( K ) i számítása ( K ) i nagyított [m 2 ] ( K ) i valódi [radián / kN ] A 1 1,083 6 2,25 2 = 0 2,0 0 2,0 10 3 2 1,083 4 1,0 1,333 = 3,0 3,0 10 3 3 1,083 2
0,25 0,667 = 2,0 2,0 10 3 0 B 0 35 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján c) Határozzuk meg a kéttámaszú tartó B támasz-keresztmetszetének hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . ( B ) elfordulási 2.21c ábra Mint tudjuk, a keresett elfordulási hatásábra a támasz-keresztmetszetben beiktatott M B = 1 er pár hatására keletkez függ leges eltolódási ábrával egyenl . A görbe vonalú hatásábra ordinátáit most is az el re kijelölt keresztmetszeteknél számítjuk ki, és ennek alapján rajzoljuk meg a hatásábrát. A nyomatéki teher módszere szerint az M B = 1 er párból megrajzolt nyomatéki ábra alapján most a A támaszelfordulást kiszámítjuk ki, majd az A támasztól kiindulva nyerjük a keresett eltolódásokat. Az eBy = 0 feltételb l nagyított értékben A = 1,333 m 2 adódik, amelyb l az ( B ) hatásábra ordinátáira az alábbi táblázat
szerinti értékeket kapjuk: ( B ) i számítása ( B ) i nagyított [m 2 ] ( B ) i valódi [radián / kN ] A 1 1,333 2 + 0,25 0,667 = 0 2,5 0 2,5 10 3 2 1,333 4 + 1,0 1,333 = 4,0 4,0 10 3 3 1,333 6 + 2,25 2 = 4,5 4,5 10 3 0 i B 0 M-2.22 Összetett tartó elmozdulási hatásábrái a) Határozzuk meg az összetett tartó K keresztmetszetének (eKy ) függ leges eltolódási hatásábráját! A tartó hajlítási merevsége a csuklótól balra EI1 = 10 4 kNm 2 , a csuklótól jobbra pedig EI 2 = 1,5 10 4 kNm 2 . A két támasztórúd húzó-nyomó merevsége megegyezik: EA1 = EA2 = 4 10 4 kN . 36 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.22 ábra Legyenek az alapul választott merevségek az alábbiak: EI 0 = EI1 = 10 4 kNm 2 , EI 2 = 1,5 EI 0 , továbbá EA0 = EA1 = EA2 = 4 10 4 kN . Eszerint i02 = EI 0 / EA0 = 0,25 m 2 37 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása
munkatételek alapján A Maxwell-féle felcserélhet ségi tétel értelmében a keresett eltolódási hatásábra a mozgó egységer által érintett tartószakasz, a „pálya” QKy = 1 er hatására keletkez függ leges eltolódási ábrájával egyenl . Ennél az összetett szerkezetnél a függ leges eltolódási ábra meghatározása nem túl egyszer&. A feladatnak többféle megoldási menete lehetséges, itt az alábbi eljárást követjük: meghatározzuk az A támasznál keletkez A abszolút, és a C csuklónál keletkez C relatív elfordulást, majd az A támasztól kiindulva számítjuk ki a pálya jelölt keresztmetszeteiben a függ leges eltolódásokat. Az elmozdulások számítására a Szilárdságtanban és a Rugalmasságtanban tanult módszereket alkalmazzuk. Most például a A támaszelfordulás meghatározására munkatételt választunk, majd annak ismeretében a C relatív elfordulást a nyomatéki teher módszerével határozzuk meg. A b) ábrán
felrajzoltuk a QKy = 1 er b l keletkez nyomatéki ábrát. Látjuk, hogy ekkor a támasztórudakban – kivételesen – nem ébrednek er k. Mivel a A támaszelfordulást munkatétellel határozzuk meg, az A támasznál beiktatunk egy M A = 1 virtuális nyomatékot, amelyhez tartozó nyomatéki ábrát és rúder ket a c) ábra mutatja. A támaszelfordulás értéke: Si Si M M 3 3 2 ds + i02 si = 0,5 = 2,121 m 2 ( ), A = ( s) 2 1 , 5 i amelyben a rúder knek nem volt szerepe. A A támaszelfordulás ismeretében az A támasztól a B támaszig terjed zárt vonalon a C relatív elfordulást abból a feltételb l számítjuk ki, hogy a B támasz az S1 rúd irányában nem mozdul el. A d) ábra értelmében: 12 8 3 = 0 , azaz 2,121 12 4,243 8 C 3 = 0 A 1 C 2 2 2 amelyb l C = 2,831 m 2 . Ezek után az (eKy ) hatásábra jelölt keresztmetszetekhez tartozó ordinátáit az A támasztól kiindulva az alábbi táblázat szerint kapjuk: i (eKy ) i számítása (eKy ) i nagyított [m 3 ] (eKy
) i valódi [mm / kN ] 1 2 3 4 5 6 2,121 0 + 4,243 2 + 3,0 2 = 2,121 3 4,243 1 = 2,121 6 4,243 4 = 2,121 9 4,243 7 + 2,831 3 = 2,121 12 4,243 10 + 2,831 6 = 2,121 15 4,243 13 + 2,831 9 = 14,486 2,120 -4,246 -2,119 0 2,135 1,4486 0,2120 -0,4246 -0,2119 0 0,2135 Megjegyezzük, hogy ugyanezt az eredményt többféle úton is megkaphatjuk. Például úgy, hogy a C relatív elfordulást is munkatétellel határozzuk meg, majd utána az eddigiekhez hasonlóan számítjuk ki a hatásábra ordinátáit. Teljesen eltér megoldási út, ha a hatásábra valamennyi ordinátáját külön-külön alkalmazott munkatétellel határozzuk meg. A tanulság ebb l az, hogy minden feladat más-más megoldási stratégiát igényel, amelynek kiválasztását a számítási munka egyszer&ségére való törekvés vezérli. 38
Igénybevételi ábra és hatásábra 1 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Mechanikai jellemz k ábrái és hatásábrái Fogalom Jelölés Definíció Hatáson minden olyan mérhet mechanikai mennyiséget (reakcióer , igénybevétel, elmozdulás) értünk, amely a tartó egy rögzített keresztmetszetében ( ) a teher helyzetének (x) a függvényében adható meg (2.1a ábra) Az igénybevételi vagy elmozdulási függvény/ábra (C ( )) leírja egy rögzített helyzet (álló) teheregyüttes hatására az adott mechanikai jellemz (C ) változását a keresztmetszet helyzetének ( ) változása függvényében (2.1b ábra) A hatásfüggvény (C ( x)) leírja a tartónak egy rögzített helyzet ( ) Hatás C Igénybevételi és elmozdulási függvény, ábra C( ) Hatásfüggvény C (x) keresztmetszetében keletkez küls vagy bels hatás változását (C ) , a (C ) mozgó egységer$ helyzetének (x) változása
függvényében (2.1c ábra) C (x) Hatásábra (C ) A hatásábra a hatásfüggvény képe. Az er - és elmozdulási hatásfüggvényeket munkatételekb l származtatjuk. Ennek rendjét foglalja össze az alábbi táblázat: Hatásfüggvények származtatása Er -hatásfüggvények Virtuális elmozdulások tétele alapján Elmozdulási hatásfüggvények Virtuális er k tétele alapján 2.1 Statikailag határozott tartók er -hatásfüggvényei a virtuális elmozdulások tétele alapján A virtuális elmozdulások tételét a Rugalmasságtan tárgy keretében tárgyaltuk. A tétel ismertetése az alkalmazásokkal együtt Kaliszky, Kurutzné és Szilágyi Szilárdságtan cím& tankönyvében található [4]. A virtuális elmozdulások tétele szerint egy er$rendszer akkor és csak akkor statikailag lehetséges (egyensúlyi), ha bármely virtuális elmozdulásrendszeren végzett munkája zérus. Er -hatásábrák készítésekor a mozgó egységteher és az általa okozott, vele
egyensúlyban lév küls és bels er k változását vizsgáljuk. A tétel értelmében az egységteher és a következtében fellép küls és bels er k tetsz leges virtuális elmozdulásrendszeren végzett munkájának összege az egységteher minden helyzetében zérus. A virtuális munka felírásához a tartón tetsz leges virtuális elmozdulásrendszert kell felvenni. A virtuális elmozdulásrendszer alapvet tulajdonsága, hogy kompatibilis, azaz 2 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján geometriailag lehetséges, vagyis elemei a geometriai egyenletek által megszabott összefüggésben állnak egymással. Ezt az elmozdulásrendszert úgy kell felvennünk, hogy a vizsgált er hatás feltétlenül munkát tudjon végezni rajta, ugyanakkor elégítse ki a tartón érvényes geometriai kerületi feltételeket. Az egységteher pedig a tartón így létrejöv virtuális elmozdulásrendszeren végez munkát. A kétféle
virtuális munka összegének - mivel az er rendszer az egységteher minden helyzetében egyensúlyban van - zérust kell adnia. Ha a vizsgált er$hatás küls$ jelleg (reakcióer$), akkor virtuális elmozdulást, ha pedig bels$ jelleg (igénybevétel), akkor virtuális alakváltozást (relatív elmozdulást) iktatunk be. Hogy a beiktatandó elmozdulásnak vagy alakváltozásnak helyet csináljunk, a tartót minden esetben át kell alakítani. Virtuális elmozdulás beiktatásához az elmozdulásnak megfelel eredeti kényszer-komponenst el kell távolítani, virtuális alakváltozás beiktatásához pedig az alakváltozási komponens jellegének megfelel en a tartón egy-szabadságfokú bels „átvágást” kell végrehajtani. Ez a beavatkozás a tartó elmozdulási (kinematikai) szabadságfokát minden esetben eggyel növeli, azaz a tartót egy fokkal fellazítja. A virtuális elmozdulás vagy alakváltozás beillesztésekor általános esetben a fellazított tartó mentén
virtuális elmozdulás-alakváltozás-rendszer jön létre. Ha a tartó statikailag határozott volt, akkor a fellazítás következtében egy-szabadságfokú, kényszermozgású láncolattá alakul, amelynek elmozdulását a beiktatott elmozdulás vagy alakváltozás egyértelm&en meghatározza. Virtuális elmozdulás beiktatása esetén a láncolat mentén csak elmozdulások jönnek létre, alakváltozások nem. Virtuális alakváltozás beiktatásakor ugyanez a helyzet, kivéve a beiktatás keresztmetszetét, ahol a beiktatott virtuális alakváltozás szinguláris alakváltozásként van jelen (csak a beiktatás helyén van alakváltozás, máshol nincs). Az egyensúlyban lév tartón a küls és bels virtuális munkaösszeg zérust ad. A virtuális küls$ munka két részb l állhat: a vizsgált küls er hatásnak (reakcióer ) a beiktatott virtuális elmozduláson végzett munkájából, valamint a tartón mozgó egységtehernek a hatásvonalába es virtuális elmozdulásokon
végzett munkájából. A virtuális bels$ munka is két részb l állhat: a vizsgált bels er hatásnak (igénybevétel) a beiktatott virtuális alakváltozáson végzett munkájából, valamint a tartón mozgó egységteherb l keletkez bels er knek (igénybevételek) a virtuális alakváltozás-rendszeren végzett munkájából. Statikailag határozott tartó esetén, amikor a beavatkozás eredményeként kialakult láncolaton nem keletkeznek virtuális alakváltozások, ez az utóbbi bels munka zérus. Mivel a tartószerkezetek terhei tipikusan gravitációs terhek, a tartón mozgó egységteher függ leges er , amely függ leges eltolódásokon végez munkát. Statikailag határozatlan tartók er -hatásfüggvényeinek az el állítása a virtuális elmozdulások tétele alapján a bels virtuális munka kiszámítása miatt nehézkes. Ezért az alábbiakban csak a statikailag határozott tartók esetével foglalkozunk. Ugyanakkor a statikailag határozatlan tartók er
hatásábráival foglalkozó fejezetekben utalni fogunk a virtuális elmozdulások tétele alapján nyerhet megoldásra is. 2.11 Küls er k (reakcióer k) hatásfüggvényei Legyen a tartón mozgó egységer F , helyzetének koordinátája x . Határozzuk meg a C küls reakcióer (C ) hatásfüggvényét! Távolítsuk el a reakcióer nek megfelel kényszerkomponenst, és iktassuk be a helyén a reakcióer vel munka-kompatibilis e virtuális elmozdulást. Ez a terhel egységer hatásvonalában v e ( x) virtuális eltolódást okoz A teljes virtuális munka most csak küls részb l áll, azaz W = Wk = F v e ( x) + C e = 0 . 3 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Figyelembe véve, hogy F = 1 , továbbá, hogy a e virtuális elmozdulás tetsz leges, ezért egységnyinek is felvehet , így a küls er hatásfüggvényére az alábbi kifejezést nyerjük (C ) = v e=1 ( x) = v e= 1 ( x) . Eszerint: Egy küls$ er$
(reakcióer$) hatásfüggvénye a támasz helyén beiktatott, a reakcióer$vel munka-kompatibilis, azzal ellentett irányú egységnyi virtuális elmozdulásból kapott, egységteher-irányú eltolódásfüggvénnyel azonos. Mivel az egységteher a gravitációs terhek esetén függ leges er , és a tartószerkezetek terhei legtöbbször ilyenek, függ leges eltolódási ábráról van szó. A beiktatott egységnyi virtuális elmozdulás pedig abszolút, így kimondhatjuk, hogy: A küls$ reakcióer$ hatásábrája a támasz helyén beiktatott, a reakcióer$vel munkakompatibilis, azzal ellentett irányú egységnyi abszolút elmozdulásból kapott függ$leges eltolódási ábra. Küls reakcióer hatásábrája esetén tehát az egységnyi abszolút elmozdulást az er pozitív irányával ellentétesen kell felvenni, hogy el jelhelyes hatásábrát kapjunk. Példaként határozzuk meg a 2.2 ábrán látható tartón a B reakcióer hatásábráját Mivel a pozitív B reakcióer felfelé
mutat, a vele munka-kompatibilis e = 1 virtuális eltolódást - a támasz eltávolítása után - lefelé vesszük fel. Az eredményként kapott függ leges eltolódási ábra az (B ) hatásábra. 2.2 ábra – Küls$ er$k hatásfüggvényei 4 Tartók statikája 2.12 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Bels er k (igénybevételek) hatásfüggvényei A helyen rögzített keresztmetszethez tartozó (C ) bels er (igénybevételi) hatásfüggvény esetén a keresztmetszetnél a bels er vel (igénybevétellel) munka-kompatibilis virtuális alakváltozást (relatív elmozdulást) iktatunk be, miután az ehhez szükséges egyszabadságfokú bels átvágást végrehajtottuk. A beiktatott virtuális alakváltozás hatására a terhel F er hatásvonalában v (x) virtuális eltolódás keletkezik. A teljes virtuális munka most küls és bels részb l áll, azaz, mivel a bels virtuális munka negatív W = Wk + Wb = F v ( x) C = 0. virtuális
alakváltozás tetsz leges, tehát egységnyinek is felvehet , így a Mivel F = 1 , és a bels er hatásfüggvénye az alábbi formát ölti (C ) = v =1 ( x ) . Eszerint: Egy keresztmetszet bels$ er$ (igénybevételi) hatásfüggvénye a keresztmetszetben beiktatott, a bels$ er$vel munka-kompatibilis egységnyi virtuális alakváltozásból kapott függ$leges eltolódásfüggvénnyel azonos. 2.3 ábra – Bels$ er$k hatásfüggvényei 5 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Mivel a beiktatott szinguláris alakváltozás nem más, mint koncentrált relatív elmozdulás, kimondhatjuk, hogy: Az igénybevételi hatásábra a keresztmetszetben beiktatott, az igénybevétellel munkakompatibilis, azzal egyez$ irányú egységnyi relatív elmozdulásból kapott függ$leges eltolódási ábra. Igénybevételi hatásábra esetén tehát az egységnyi relatív elmozdulást az igénybevétel pozitív irányával megegyez en kell
felvenni, hogy el jelhelyes hatásábrát kapjunk. Példaként határozzuk meg a 2.3 ábrán látható tartó koordinátájú K keresztmetszetének nyomatéki hatásábráját. Ehhez a keresztmetszetnél csuklót iktatunk be, majd létrehozzuk a pozitív nyomatékkal egyez irányú = 1 relatív elfordulást. Az így létrejött függ leges eltolódási ábra a keresett ( M K ) hatásábra. Az ábrán feltüntettük a gerendának a keresztmetszetben elképzelt differenciálisan kicsiny hosszúságú szakaszát, a Szilárdságtanból jól ismert rúdelemet, amelynek mindkét véglapjára felrajzoltuk a pozitív keresztmetszeti nyomatékot. Látható, hogy a beiktatott relatív elfordulás el jele a nyomatékéval megegyezik. Az egyes igénybevételi fajtáknak megfelel en beiktatandó egy-szabadságfokú bels kapcsolatokat és relatív elmozdulásokat az alábbi táblázatban foglaljuk össze a 2.4 ábrával összhangban, ahol ugyancsak a keresztmetszetnél kimetszett rúdelemre
rajzoltuk fel a pozitív igénybevételeket. 2.4 ábra - A relatív elmozdulásnak megfelel$ egy-szabadságfokú bels$ kapcsolat 6 Tartók statikája Hatásfüggvény, hatásábra 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Jele A beiktatott alakváltozás (relatív elmozdulás) Az egy-szabadságfokú bels átvágást biztosító kapcsolat Normáler Nyíróer Hajlítónyomaték Rúder 2.13 kizárólag tengelyirányú relatív eltolódást engedélyez görg (TK ) kizárólag tengelyre mer leges relatív eltolódást engedélyez görg kizárólag relatív elfordulást (M K ) engedélyez csukló ( S ij ) kizárólag tengelyirányú relatív eltolódást engedélyez görg (N K ) egységnyi koncentrált relatív eltolódás a rúd tengelye (érint je) irányában egységnyi koncentrált relatív eltolódás a rúd tengelyére (érint jére) mer legesen egységnyi koncentrált relatív elfordulás (érint k törése), forgáspont a rúd
tengelyében egységnyi koncentrált relatív eltolódás a rúd tengelye irányában Egy-szabadságfokú láncolatok eltolódási ábrái Amint láttuk, a statikailag határozott síkbeli tartók er -hatásábrái egy-szabadságfokú síkbeli láncolatok függ leges eltolódási ábráira vezetnek. A síkbeli láncolatok több merev tárcsából állnak, amelyeket síkbeli kényszerekkel, legtöbbször csuklókkal kapcsolunk egymáshoz és az aljzathoz. Egyszer& feladatok esetén felírhatjuk a függ leges eltolódási ábra függvényét is, amely a hatásfüggvénnyel azonos. Minthogy a hatásábra poligon, a keresztmetszetnél szingularitással, a vonatkozó hatásfüggvény nem folytonos, azaz ún. nemsima függvény Az ilyen függvényeket szakaszonként külön-külön függvényekkel adják meg, a függvényt alkotó rész-függvények halmazát kapcsos jellel rendelve egymáshoz. Az alkalmazási gyakorlatban azonban a kézi számításokhoz közvetlenül a hatásábrát
állítják el , míg magára a hatásfüggvényre a számítógépes algoritmusok készítésénél van szükség. A láncolatok függ leges eltolódási ábráit számítással és szerkesztéssel határozhatjuk meg. A számítással történ megoldás a Statika és a Szilárdságtan tantárgyakban tanult módon történik [3,4]. Az elmozdulásokra vonatkozó alapösszefüggések szerint Valamely keresztmetszet (j) abszolút elmozdulásai ( keresztmetszet (i) abszolút elmozdulásainak ( ( ij , u kl ) az együttesével. i j , e j ) egyenérték ek egy megel$z$ , ei ) és a köztük lév$ relatív elmozdulásoknak A zárt vonal relatív elmozdulásai együtt ( ij , u kl ) egyenérték ek nullával. E két összefüggés alapján a vizsgált láncolat tetszés szerinti elemének, pontjainak elmozdulásai kiszámíthatók, és maga az eltolódási ábra is felrajzolható. Ha a láncolatok függ leges eltolódási ábráit szerkesztéssel kívánjuk meghatározni, akkor a fenti
összefüggéseket szerkesztéshez szükséges formában kell megfogalmaznunk. A szerkesztés a láncolati pólusok közötti összefüggéseken alapszik. A keresztmetszet abszolút elmozdulásának ( i , ei ) elfordulás-középpontját abszolút pólusnak (i), relatív elmozdulásának 7 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján ( jk , u jk ) elfordulás-középpontját relatív pólusnak (j,k) nevezzük. Az elmozdulásoknál megszokott módon az abszolút pólust egy jellel (bet&vel, számmal), a relatív pólust két jellel jelöljük, a vonatkozó tárcsák jelére utalva. A jeleket kerek zárójelbe tesszük A pólusokra vonatkozó összefüggések az elmozdulásokra vonatkozó összefüggésekkel összhangban: Az i-edik tárcsa (i ) abszolút pólusa és a j-edik tárcsa ( j ) abszolút pólusa a két tárcsa (i, j ) relatív pólusával egy egyenesen van. Az (i, j ) , ( j , k ) és (i, k ) relatív pólusok egy
egyenesen vannak. Az els állítás jelölése: (i ), ( j ) (i, j ) vagy (i ), (i, j ) ( j) vagy ( j ), (i, j ) (i ) A második állítással egyenérték& jelölések: (i, j ), ( j , k ) (i, k ) , vagy (i, j ), (i, k ) ( j , k ) , vagy (i, k ), ( j , k ) (i, j ) E két összefüggés segítségével a láncolat elmozdulási ábrája megszerkeszthet , azaz a szerkesztéshez szükséges hiányzó abszolút vagy relatív pólusok megkereshet k. A szerkesztés során a hatásábra jellemz ordinátái geometriai úton meghatározhatók. További, a fentiekb l következ állítások: - Az abszolút pólus nem mozdul el, ezért képe az eltolódási ábra zérustengelyén van. - Az a tárcsa, amelyen egynél több abszolút pólust lehet kimutatni, nem mozdul el, képe a zérustengellyel esik egybe. - Ha egy tárcsa abszolút pólusa a végtelenben van, a tárcsa önmagával párhuzamosan tolódik el. - Ha két tárcsa relatív pólusa a végtelenben van, a két tárcsa
egymással párhuzamosan mozdul el. - Abszolút eltolódás pólusa az eltolódásra mer leges egyenesen van. - Relatív eltolódás pólusa az eltolódásra mer legesen a végtelenben van. Az egy-szabadságfokú láncolatok abszolút és relatív pólusai közötti összefüggéseket illusztrálja a 2.5a, b, c és d ábra 8 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.5 ábra - Egy-szabadságfokú láncolatok abszolút és relatív pólusai közötti összefüggések 2.14 Mintapéldák: Er -hatásábrák a virtuális elmozdulások tétele alapján Amint láttuk, a hatásábra-készítés lényegében a beiktatott egységnyi abszolút vagy relatív elmozdulás hatására a láncolat függ leges eltolódási ábrájának elkészítéséb l áll. Ez számítással és szerkesztéssel történhet. Láncolatok elmozdulásainak számítással történ meghatározását a Statikában és a Szilárdságtanban részletesen
ismertettük. Az alábbiakban a számítással és szerkesztéssel történ megoldás lépéseit foglaljuk össze. Statikailag határozott tartók küls és bels er -jelleg& hatásábráinak virtuális elmozdulások tétele (vagy a gyakorlatban elterjedt kifejezéssel: kinematikai módszer) alapján történ meghatározása lépéseit számítás és szerkesztés alapján az alábbi táblázatokban foglaljuk össze. Az er -hatásábra-készítés lépései számítással 1. 2. 3. A meghatározandó küls , vagy bels er nek megfelel en átalakítjuk a tartót: vagy eltávolítjuk a reakcióer nek megfelel küls kényszerkomponenst, vagy beiktatjuk az igénybevételnek megfelel egy-szabadságfokú bels átvágást biztosító kapcsolatot. Ezáltal kialakítottuk az egy-szabadságfokú láncolatot. Az így kialakult láncolaton kinematikai teherként beiktatjuk az egységnyi abszolút elmozdulást a pozitív küls er vel ellentétesen, illetve az egységnyi relatív elmozdulást a
pozitív igénybevétellel megegyez en. A láncolatok elmozdulásaira vonatkozó egyenérték&ségek alapján kiszámítjuk a függ leges eltolódási ábra – a keresett hatásábra – jellemz ordinátáit. Ha szükséges, az ordináták segítségével felírhatjuk a hatásfüggvény szakaszonként lineáris függvényét is. 9 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Az er -hatásábra-készítés lépései szerkesztéssel 1. 2. 3. 4. 5. 6. 7. A meghatározandó küls , vagy bels er nek megfelel en átalakítjuk a tartót: vagy eltávolítjuk a reakcióer nek megfelel küls kényszerkomponenst, vagy beiktatjuk az igénybevételnek megfelel egy-szabadságfokú bels átvágást biztosító kapcsolatot. Ezáltal kialakítottuk az egy-szabadságfokú láncolatot. Az így kialakult láncolaton beszámozzuk a tárcsákat, és a hozzájuk tartozó – közvetlenül megállapítható – abszolút és relatív
pólusokat. Szabadon felvesszük egy olyan tárcsa kimozdult képét, amelyik a kívánt egységnyi elmozduláshoz kapcsolódik. A kimozdított tárcsához viszonyítva beillesztjük az egységnyi abszolút elmozdulást a pozitív küls er vel ellentétesen, illetve az egységnyi relatív elmozdulást a pozitív igénybevétellel megegyez en. Megszerkesztjük a láncolat, pontosabban a „pályát” alkotó tárcsák elmozdult képét, (azon tárcsákét, amelyeket a mozgó egységer útja során érint). Ehhez megkeressük a szükséges abszolút és relatív pólusokat, felhasználva a pólusokra vonatkozó összefüggéseket. Végül megszerkesztjük a zérustengelyt, amely az abszolút pólusok képének geometriai helye. A hatásábrát a pályát alkotó tárcsák képe és a zérustengely közötti tartomány alkotja. Az így el állított hatásábrának számszer&en meghatározzuk a szükséges jellemz ordinátáit. M-2.11 Kéttámaszú konzolos tartó igénybevételi
és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a kéttámaszú tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.11a ábra 10 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A küls és bels virtuális munkák összege zérus (a bels mindig negatív): F v( x) M K ( x) K = 0, ahol F a tartón mozgó, x helyzet& egységer , v(x) a K keresztmetszetben beiktatott K virtuális relatív elfordulásból keletkez függ leges eltolódási ábra, és M K ( x) a keresztmetszeti nyomaték F er helyzetét l függ en változó értéke, maga a hatásábra: M K ( x) = ( M K ) . Mivel F = 1, és K = 1 , így a keresztmetszet nyomatéki hatásábrája a keresztmetszeti nyomatékkal munka-kompatibilis egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos: ( M K ) =
v( x) . A nyomatéknak megfelel en tehát átalakítjuk a tartót: csuklót teszünk be a keresztmetszetnél, hogy a relatív elfordulást beiktathassuk. Ekkor a tartó egy-szabadságfokú láncolattá alakul Beszámozzuk a tárcsákat, és a közvetlenül megállapítható abszolút és relatív pólusokat. A fix támasz csuklója a II. jel& tárcsa (2) abszolút pólusa, a két tárcsát összekapcsoló csukló pedig az (1,2) relatív pólus. Az (1) abszolút pólus a görg s megtámasztásnál keletkez abszolút eltolódásra mer leges egyenesen helyezkedik el, ugyanakkor a (2) abszolút és az (1,2) relatív pólusok által meghatározott egyenesen is rajta kell lennie, azaz (2), (1,2) (1) , így az (1) abszolút pólus a két egyenes metszéspontjában, a görg s megtámasztási pontban van. Ezután szabadon felvesszük például az I. tárcsa képét, azaz elmozdult helyzetét, amelyre levetítjük az (1,2) relatív pólust. Itt beiktatjuk a K = 12 = 1 relatív elfordulást
úgy, hogy a II. tárcsát a pozitív nyomatéknak megfelel el jellel fordítjuk el az I tárcsához képest Mivel az II. tárcsa a bal oldali tartórész, a balról számított igénybevételek el jelszabálya szerint a pozitív nyomatéknak megfelel en ez az óra járásával megegyez elfordítást jelenti. (Ha a II. tárcsa képét vesszük fel kiindulásként, és ehhez képest az I tárcsát fordítjuk el, amely a jobb oldali tartórésznek felel meg, akkor a jobb oldali el jelszabály szerint az óra járásával ellentétes elfordítást kell alkalmaznunk. Ez természetesen ugyanazt az alakzatot eredményezi.) Ekkor tehát megkapjuk a tárcsák elmozdult alakját, már csak a nullvonalat kell megszerkesztenünk. Az eltolódási ábra nullvonala a helyben maradó, el nem mozduló pontok geometriai helye. Az abszolút pólusok nem mozdulnak el, így azokat levetítve, majd összekötve, megkapjuk a nullvonalat és egyben a függ leges eltolódási ábrát, azaz az ( M K )
hatásábrát. A szerkesztéssel kapott ábra ordinátáit a 12 = 1 elfordulásból számíthatjuk, hiszen távolságra a támasz alatt ugyancsak nagyságú eltolódás keletkezik, amelyb l már attól bármely ordináta számítható. b) Határozzuk meg a kéttámaszú tartó K keresztmetszetének (TK ) hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer A küls és bels virtuális munkák összege most (a bels mindig negatív): F v( x) TK ( x) u K = 0 , ahol v(x) most a K keresztmetszetben beiktatott u K virtuális relatív eltolódásból származó függ leges eltolódási ábra. Mivel F = 1, u K = 1 és TK ( x) = (TK ) , így a keresztmetszet nyíróer hatásábrája a keresztmetszeti nyíróer vel munka-kompatibilis egységnyi relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos: (TK ) = v( x) . 11 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.11b ábra
Most tehát a nyíróer nek megfelel en alakítjuk át a tartót: görg s kapcsolatot teszünk be a keresztmetszetnél úgy, hogy a nyírásirányú relatív eltolódást beiktathassuk. Ekkor a tartó ugyancsak egy-szabadságfokú láncolattá alakul. Beszámozzuk a tárcsákat, és a közvetlenül megállapítható abszolút és relatív pólusokat. A fix támasz csuklója most is a II jel& tárcsa (2) abszolút pólusa, azonban az (1,2) relatív pólus most a u K eltolódásra mer legesen a végtelenben van, mivel a két tárcsa párhuzamosan mozdul el. Az (1) abszolút pólus most is a görg s támasz támasztási felületére mer leges egyenesen helyezkedik el, ugyanakkor a (2) abszolút és az (1,2) relatív pólusok által meghatározott egyenesen is rajta kell lennie, vagyis (2), (1,2) (1) , így az (1) abszolút pólus a két egyenes metszéspontjában, a görg s megtámasztási pontban van. Vegyük fel az I. tárcsa képét, azaz elmozdult helyzetét Ez után beiktatjuk a
u K = u12 = 1 relatív eltolódást úgy, hogy a bal oldali II. tárcsát a pozitív nyíróer nek megfelel el jellel párhuzamosan eltoljuk az I. tárcsához képest Mivel a II tárcsa a bal oldali tartórész, az igénybevételek el jelszabálya szerint ez a II. tárcsa felfelé való eltolását jelenti (Ha a II. tárcsa képét vesszük fel kiindulásként, akkor a jobb oldali I tárcsát a jobboldali el jelszabály szerint lefelé kell eltolni, amely természetesen ugyanazt az alakzatot eredményezi.) Ezáltal megkapjuk a tárcsák elmozdult alakját, majd az abszolút pólusokat levetítve és összekötve megkapjuk a nullvonalat, és egyben a függ leges eltolódási ábrát, azaz az (TK ) hatásábrát. A szerkesztéssel kapott ábra bármely ordinátája egyszer&en számítható c) Határozzuk meg a kéttámaszú tartó A támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! ( A) A virtuális munkaösszeg most
csak küls munkákból áll: F v( x) + A( x) u A = 0 , ahol v(x) a függ leges eltolódási ábra az A támasznál beiktatott u A virtuális abszolút eltolódásból. Mivel F = 1, u A = 1 és A( x) = ( A) , így az A támaszer hatásábrája a támaszer vel munka-kompatibilis egységnyi abszolút eltolódásból rajzolt függ leges eltolódási ábra ellentettjével azonos: ( A) = v( x) , 12 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.11c ábra ezért a pozitív reakcióer vel ellentétesen, lefelé mutatóan kell beiktatni a virtuális eltolódást. Most a reakcióer nek megfelel en alakítjuk át a tartót: eltávolítjuk a megtámasztást, hogy az abszolút eltolódást beiktathassuk. Ekkor a tartó olyan egy-szabadságfokú láncolattá alakul, amely mindössze egyetlen tárcsából áll. Az (1) abszolút pólus most is a görg s megtámasztás megtámasztási felületére mer leges egyenesen helyezkedik el, ezt
levetítve a kimozdított tárcsa képére megkapjuk a tárcsa helyben maradó, nullvonalon lév pontját. A nullvonal másik pontját az A támasznál beiktatott egységnyi eltolódás kezd pontja jelöli ki. Ezáltal megkapjuk a függ leges eltolódási ábrát, azaz az ( A) hatásábrát. A szerkesztéssel kapott ábra bármely ordinátája egyszer&en számítható. M-2.12 Gerber-tartó igénybevételi és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a Gerber-tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! A keresztmetszet nyomatéki hatásábrája a keresztmetszeti nyomatékkal munkakompatibilis egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél csuklót teszünk be, hogy a relatív elfordulást beiktathassuk. Ekkor a tartó három tárcsából álló egy-szabadságfokú
láncolattá alakul. Beszámozzuk a tárcsákat A fix támasz csuklója a középs , II. jel& tárcsa (2) abszolút pólusát adja meg, míg a két széls tárcsához csatlakozó csukló az (1,2) és a (2,3) relatív pólusokat jelöli ki. Az (1) és (3) abszolút pólusok a megfelel görg s megtámasztások megtámasztási felületére mer leges egyenesen helyezkednek el. Ugyanakkor az (1) pólusnak a (2) abszolút és az (1,2) relatív, a (3) pólusnak pedig a (2) abszolút és a (2,3) relatív pólusok által meghatározott egyenesen is rajta kell lennie, azaz (2), (1,2) (1) , illetve (2), (2,3) (3) . Így az (1) és (3) abszolút pólusok a megfelel görg s megtámasztási pontokban vannak. 13 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.12a ábra Szabadon felvesszük vagy a II., vagy a III tárcsa képét, majd beiktatjuk a = K 23 = 1 virtuális relatív elfordulást a pozitív nyomatéknak megfelel en. Ezután
levetítjük a (2) és (3) abszolút pólusokat a II. és III tárcsák képére, ezáltal megkapjuk a nullvonalat. A nullvonalra levetítve az (1) abszolút pólust, az I tárcsa egy pontját kapjuk, míg a másik pontját a II. tárcsa képére levetített (1,2) relatív pólus adja E két pontot összekötve megkapjuk az I. tárcsa képét is, és ezáltal el állítottuk az ( M K ) hatásábrát A hatásábra ordinátáit a 23 = 1 elfordulásból kiindulva számíthatjuk. b) Határozzuk meg a Gerber-tartó egy másik keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (TK ) nyíróer 2.12b ábra A keresztmetszet nyíróer hatásábráját a keresztmetszeti nyíróer vel munkakompatibilis egységnyi relatív eltolódásból rajzolt függ leges eltolódási ábra adja. Most tehát a nyíróer nek megfelel görg s kapcsolatot teszünk be a keresztmetszetnél. Ekkor a tartó ugyancsak három tárcsából álló egy-szabadságfokú
láncolattá alakul. Beszámozzuk a tárcsákat. Mivel a III tárcsa két pontjában is meg van támasztva, nem mozdul el, vagyis minden pontja abszolút pólus. Ezért a III tárcsa tetsz legesen felvett képe a nullvonallal esik 14 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján egybe. A u K = u 23 = 1 virtuális relatív eltolódás beiktatásakor a jobbra lév II tárcsát lefelé kell párhuzamosan eltolni. Az I tárcsa képét a II tárcsa képére levetített (1,2) relatív, és a nullvonalra levetített (1) abszolút pólusok összekötése adja meg. Ezáltal megkaptuk a függ leges eltolódási ábrát, azaz az (TK ) hatásábrát. A hatásábra bármely ordinátája egyszer&en számítható. c) Határozzuk meg a Gerber-tartó befüggesztett tartórészén lév keresztmetszetének (TK ) nyíróer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.12c ábra A keresztmetszetnél beiktatott
görg s kapcsolatot a tartót ugyancsak három tárcsából álló egy-szabadságfokú láncolattá alakítja. A III tárcsa most is mozdulatlan, mivel két pontjában is meg van támasztva, tehát minden pontja abszolút pólus. A tárcsa tetsz legesen felvett képe tehát a nullvonal, amelyen most a (2,3) relatív pólus is rajta van. A u K = u12 = 1 virtuális relatív eltolódás beiktatásakor az I. és II tárcsákat egymástól egységnyire párhuzamosan eltoljuk, majd az (1) abszolút és a (2,3) relatív pólusok nullvonalra való levetítésével megkapjuk a hatásábrát. A hatásábra bármely ordinátája ezután egyszer&en számítható. d) Határozzuk meg a Gerber-tartó B támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (B ) 2.12d ábra 15 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A B támaszer hatásábrája a támaszer vel ellentett,
azzal munka-kompatibilis egységnyi abszolút eltolódásból rajzolt függ leges eltolódási ábrával azonos. A reakcióer nek megfelel en eltávolítjuk a megtámasztást, ekkor a tartó két tárcsából álló egy-szabadságfokú láncolattá alakul. Az (1) és (2) abszolút pólusok a görg s megtámasztás megtámasztási felületére mer leges egyenesen helyezkednek el. Vegyük fel a II tárcsa képét a pozitív reakcióer vel ellentétesen, a lefelé mutatóan beiktatott e B = e B = 1 virtuális eltolódásnak megfelel en. A (2) pólust levetítve a tárcsa képére, megkapjuk a tárcsa helyben maradó, nullvonalon lév pontját. A nullvonal másik pontját a B támasznál beiktatott egységnyi eltolódás kezd pontja jelöli ki. Megrajzolva a nullvonalat, és levetítve rá az (1) pólust, az I tárcsa egyik pontját kapjuk meg. A másik pontját az (1,2) relatív pólus II tárcsára levetített képe adja. Így megkapjuk a függ leges eltolódási ábrát, azaz az (B )
hatásábrát Az ordináták az e B = 1 eltolódás alapján számíthatók. M-2.13 Háromcsuklós tartó igénybevételi hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján a) Határozzuk meg a háromcsuklós tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13a ábra A keresztmetszet nyomatéki hatásábrája a keresztmetszetben beiktatott egységnyi relatív elfordulásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott csukló hatására a tartó három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói az I., illetve a III tárcsa megfelel abszolút pólusát adják meg, míg az eredeti és a beiktatott közbens csuklók az (1,2) és a (2,3) relatív pólusokat jelölik ki. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a levetített (2,3) relatív forgáspontban a pozitív
nyomatéknak megfelel en elfordítjuk hozzá képest a másik tárcsát K = 23 = 1 értékkel. A nullvonalhoz a (3) abszolút póluson kívül a (2)-re is szükségünk van. Ezt az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések által meghatározott egyenesek metszéspontja adja meg. Levetítve az abszolút pólusokat a 16 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét a nullvonalon lév (1) abszolút és a II. tárcsára levetített (1,2) abszolút pólus összekötése adja meg, és ezáltal el állítottuk az ( M K ) hatásábrát. A hatásábra ordinátáit a 23 = 1 elfordulásból kiindulva számíthatjuk. b) Határozzuk meg a háromcsuklós tartó K keresztmetszetének (TK ) nyíróer hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13b ábra A keresztmetszet nyíróer hatásábrája a
keresztmetszetben beiktatott egységnyi nyírásirányú relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó ugyancsak három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói most is az I, illetve a III tárcsa megfelel abszolút pólusát adják meg, míg a közbens csukló alkotja az (1,2) relatív pólust, azonban a (2,3) relatív pólus a beiktatott görg s kapcsolat által meghatározott elmozdulási irányra mer legesen a végtelenben van, mivel a II. és a III tárcsa csak egymással párhuzamosan mozdulhat el. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, a görg s kapcsolat mentén eltolva ket egymáshoz képest a pozitív nyíróer nek megfelel en u K = u 23 = 1 értékkel. Mivel azonban nekünk az alkalmazott munkatétel értelmében a függ leges eltolódások ábrájára van szükségünk, az ábrán a tárcsákat u Ky
= u 23, y = 2 / 2 mértékben toljuk el egymáshoz képest függ legesen. A nullvonalhoz most is szükségünk van a (2) pólusra, amelyet most is az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések által meghatározott egyenesek metszéspontja határoz meg. Levetítve az abszolút pólusokat a megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét most is a nullvonalon lév (1) abszolút és a II. tárcsa képére levetített (1,2) relatív pólus összekötése adja meg, és ezáltal megkapjuk az (TK ) hatásábrát. Ezután kiszámítjuk a hatásábra ordinátáit. 17 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján c) Határozzuk meg a háromcsuklós tartó K keresztmetszetének ( N K ) normáler hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.13c ábra A keresztmetszet normáler hatásábrája a keresztmetszetben beiktatott egységnyi tengelyirányú
relatív eltolódásból rajzolt függ leges eltolódási ábrával azonos. A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó most is három tárcsából álló egy-szabadságfokú láncolattá alakul. A fix támaszok csuklói most is az I, illetve a III tárcsa megfelel abszolút pólusát adják meg, míg a közbens csukló alkotja az (1,2) relatív pólust, de most a (2,3) relatív pólus a beiktatott görg s kapcsolatnál a rúd tengelyére mer legesen a végtelenben van, mivel a II. és a III tárcsa tengelyirányban mozdul el egymással párhuzamosan. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén tengelyirányban eltoljuk ket egymáshoz képest a pozitív normáler nek megfelel en u K = u 23 = 1 értékkel. Az alkalmazott munkatétel értelmében a függ leges eltolódások ábrájára van szükségünk, ezért az ábrán a tárcsákat u Ky = u 23, y = 2 / 2 mértékben toljuk el egymáshoz képest függ
legesen. A nullvonalhoz most is szükségünk van a (2) pólusra, amely azonban az (1), (1,2) (2) és a (3), (2,3) (2) összefüggések szerint most a végtelenben van, ami azt jelenti, hogy a II. tárcsa a nullvonallal párhuzamos kell legyen Mivel azonban a III. tárcsa képére levetített (3) abszolút pólusnak a nullvonalon kell lennie, és a III. tárcsa a II tárcsával párhuzamos, következésképpen a III tárcsa maga a nullvonal Így a levetített (1) pólus is rajta van, amelyb l a II. tárcsára levetített (1,2) relatív pólus segítségével az I. tárcsa képét, és így az ( N K ) hatásábrát is megkapjuk Ezután kiszámítjuk a hatásábra ordinátáit. 18 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.14 Rácsos tartó rúder hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján Határozzuk meg az alsópályás rácsos tartó jelölt három rúder szerkesztéssel!
hatásábráját 2.14a ábra a) Határozzuk meg az alsópályás rácsos tartó ( S1 ) rúder hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.14b ábra Ehhez átvágjuk a rudat, és a rúd átvágott végei között egységnyi pozitív relatív eltolódást hozunk létre, majd ebb l meghatározzuk a tartón végigmen egységer pályájának, az alsó pályának a függ leges eltolódási ábráját, amely a keresett hatásábrát adja. Az átvágás a rácsos tartót két merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A II tárcsa (2) abszolút pólusa a fix támasz csuklóközéppontja, az (1,2) relatív pólus a két tárcsát összeköt csuklóban van. Az (1) abszolút pólus a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van, de mivel (2), (1,2) (1) , így a görg s támasz csuklóközéppontjában van. Az átvágott rúd két vége között úgy tudjuk legegyszer&bben beiktatni az egységnyi
pozitív relatív eltolódást, ha az (1,2) relatív elfordulás-középpontban az I. és a II tárcsát elfordítjuk egymáshoz képest olymódon, hogy a rúdban éppen a u = u1 = 1 pozitív eltolódás (nyúlás) keletkezzék. Ehhez a relatív elfordulásnak éppen 12 = u1 / 4 = 1 / 4 nagyságúnak kell 19 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján lennie. Vegyük fel tetsz legesen például az I (vagy a II) tárcsa képét, és fordítsuk el hozzá képest a másik tárcsát a 12 = 1 / 4 értékkel úgy, hogy a rúdban nyúlást okozzon. Ezután levetítjük a tárcsákra az abszolút pólusaikat, és berajzoljuk a nullvonalat. Ezáltal megkaptuk a hatásábrát. b) Határozzuk meg az (S 2 ) elmozdulások tétele alapján! rúder hatásábrát is szerkesztéssel, a virtuális 2.14c ábra A ferde rácsrúd átvágása a rácsos tartót négy merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A IV
tárcsa (4) abszolút pólusát a fix támasz csuklóközéppontja adja, míg az (1) abszolút pólus a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2), (1,3), (2,4) és (3,4) relatív pólusokat. Mivel az alsó pálya mentén (2,4), (1,2) (1,4) , ugyanott (4), (1,4) (1) , így az (1) abszolút pólus a görg s támasz csuklóközéppontjában van. Most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be az átvágott rúd két vége között az egységnyi pozitív relatív eltolódást: vagy az (1,2), vagy a (3,4) pólusban. A szükséges relatív elfordulásnak 12 = 34 = u 2 / k = 1 / k nagyságúnak kell lennie, ahol k = 3 / 2 az (1,2) vagy (3,4) pólusok mer leges távolsága az átvágott rúdtól. Mivel alsópályás tartóról van szó, vegyük fel tetsz legesen az I. tárcsa képét, és fordítsuk el hozzá képest a II. tárcsát a 12 = 2 / 3 értékkel úgy,
hogy a rúdban nyúlást okozzon A nullvonal meghatározásához szükségünk van a (2) abszolút pólusra is. A (4), (2,4) (2) és az (1), (1,2) (2) összefüggésekb l megtudjuk, hogy a (2) abszolút pólus az alsó öv vonalán helyezkedik el valahol. Hogy pontosan hol, azt a (3) abszolút pólus segítségével tudhatjuk meg. A (3) pólus helyét a (4), (3,4) (3) és az (1), (1,3) (3) összefüggésekb l kapjuk meg Az (1,2), (1,3) (2,3) és a (2,4), (3,4) (2,3) összefüggésekb l megtudjuk, hogy a (2,3) relatív pólus függ legesen a végtelenben van, ami arra utal, hogy a II. és a III tárcsa párhuzamosan mozdul el. Ugyanakkor most már a (3), (2,3) (2) összefüggés kimetszi a (3) pólus függ legesében a (2) pólus keresett helyét az alsó övön. Ezután levetítjük az I és II tárcsákra az abszolút pólusaikat, és berajzoljuk a nullvonalat. A IV tárcsa hiányzó képét a (4) és (2,4) pólusok levetítéséb l kapjuk meg. Ezáltal megkaptuk az alsópályás
tartó keresett 20 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján rúder hatásábráját. Fels pályás esetben ugyanezt a hatásábrát kapjuk, mivel a II és a III tárcsa képe megegyezik. c) Határozzuk meg az ( S 3 ) rúder elmozdulások tétele alapján! hatásábrát is szerkesztéssel, a virtuális 2.14d ábra A tartó szimmetriatengelyében lév oszlop átvágása révén a rácsos tartó most is négy merev tárcsából álló egy-szabadságfokú láncolattá alakul. A IV tárcsa (4) abszolút pólusát a fix támasz csuklóközéppontja adja. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2), (1,4), (2,3) és (3,4) relatív pólusokat. Az (1) abszolút pólus most is a görg s megtámasztásnál keletkez eltolódásra mer leges egyenesen van, de most a (4), (1,4) (1) összefüggésb l feljebb, a tartó felett helyezkedik el. Az átvágott rúd két vége között az egységnyi pozitív relatív
eltolódást most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be: vagy az (1,2), vagy a (3,4) pólusban. A szükséges relatív elfordulásnak most 12 = 34 = u3 / 3 = 1 / 3 nagyságúnak kell lennie. Vegyük fel tetsz legesen az I tárcsa képét, és fordítsuk el hozzá képest a II tárcsát a 12 = 1 / 3 értékkel úgy, hogy a rúdban nyúlást okozzon. A nullvonal meghatározásához szükségünk van a (2) abszolút pólusra is. A (4), (3,4) (3) és a (3), (2,3) (2) összefüggésekb l megtudjuk, hogy a (2) abszolút pólus az alsó öv vonalán helyezkedik el. Pontos helyét az (1), (1,2) (2) összefüggésb l kapjuk meg, amely szerint egybeesik az (1,2) relatív pólussal. Ez azt jelenti, hogy az I tárcsa képén az (1) és a (2) abszolút pólus egyaránt rajta van, tehát az I. tárcsa képe a nullvonal A (4), (3,4) (3) , (1,4), (3,4) (1,3) és az (1), (1,3) (3) állításokból megkapjuk, hogy a (3) pólus egybeesik a (3,4) pólussal, tehát a
IV. tárcsa képe is a nullvonalon van A (23) és a (3,4) pólusok levetítésével megkapjuk a III tárcsa képét, és ezzel a keresett hatásábrát is. Látható, hogy alsópályás esetben a hatásábra a pálya vonalának, azaz az I., II, III és IV tárcsák elmozdulási alakzatából áll Fels pályás esetben azonban csak az I. és II tárcsa elmozdulási vonala kell, amely a nullvonalat alkotja Valóban, fels pályás esetben a vizsgált rúd vakrúd. 21 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.15 Vonórudas tartó igénybevételi hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján (TK ) a) Határozzuk meg a vonórudas tartó K keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer 2.15a ábra A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó négy tárcsából álló egy-szabadságfokú láncolattá alakul. A
fix támasz csuklója a III tárcsa (3) abszolút pólusát adja meg, míg a közbens csuklók alkotják az (1,2), (1,4) és (3,4) relatív pólusokat. A (2,3) relatív pólus a beiktatott görg s kapcsolat által meghatározott elmozdulási irányra mer legesen a végtelenben van. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén eltoljuk ket egymáshoz képest a pozitív nyíróer nek megfelel en u K = u 23 = 1 értékkel. A függ leges eltolódási ábrában ez u 23, y = cos vetületként jelenik meg, ahol a vizsgált tartószakasz vízszintessel bezárt szöge. A nullvonalhoz szükségünk van a (2) pólusra, amelyet a (3), (2,3) (2) és az (1), (1,2) (2) összefüggések által meghatározott egyenesek metszéspontja határoz meg. Ehhez azonban el z leg az (1) pólus helyét meg kell határoznunk a görg s megtámasztás függ legesében. Ezt a (3,4), (1,4) (1,3) és az (1,2), (2,3) (1,3) , majd a (3), (1,3) (1) metszéspontok
adják meg. Levetítve a (2) és (3) abszolút pólusokat a megfelel tárcsák képére, megkapjuk a nullvonalat. Végül az I tárcsa képét a nullvonalon lév (1) és a II. tárcsa képére levetített (1,2) pólus összekötése adja meg, így megkapjuk az (TK ) hatásábrát. 22 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján b) Határozzuk meg a vonórudas tartó K keresztmetszetének ( N K ) normáler hatásábráját is szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.15b ábra A keresztmetszetnél beiktatott görg s kapcsolat hatására a tartó most is négy tárcsából álló egy-szabadságfokú láncolattá alakul, most azonban a (2,3) relatív pólus a beiktatott görg s kapcsolatnál a rúd tengelyére mer legesen van a végtelenben. Tetsz legesen felvesszük a II. vagy a III tárcsa kimozdult alakját, és a görg s kapcsolat mentén tengelyirányban eltoljuk ket egymáshoz képest a pozitív
normáler nek megfelel en u K = u 23 = 1 értékkel, ami a függ leges eltolódási ábrában u 23, y = sin értékben jelenik meg. A nullvonalhoz most is szükségünk van a (2) pólusra, amelyet az alábbi összefüggések alapján szerkeszthetünk meg: (1,4), (3,4) (1,3) és (1,2), (2,3) (1,3) , majd (3), (1,3) (1) , végül (1), (1,2) (2) és (3), (2,3) (2) . A (2) és (3) abszolút pólusok levetítésével megkapjuk a nullvonalat, majd az (1) és (1,2) pólusok levetítésével az I. tárcsa képét. Ezzel elkészült a keresett ( N K ) hatásábra c) Határozzuk meg a vonórúdban keletkez er virtuális elmozdulások tétele alapján! (S ) hatásábráját is szerkesztéssel, a A vonórúd átvágásával a tartó most is négy tárcsából álló egy-szabadságfokú láncolattá alakul, most azonban a (3,4) relatív pólus a vonórúd tengelyére mer legesen van a végtelenben. 23 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek
alapján 2.15c ábra A vonórúdban beiktatásra kerül egységnyi pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük az I vagy a II. tárcsa kimozdult alakját, és elfordítjuk egymáshoz képest ket 12 = 1 / h szöggel úgy, hogy a vonórúdban egységnyi nyúlás keletkezzen. Az (1) és (2) abszolút pólusok levetítésével megrajzoljuk a nullvonalat, és ezzel kész a keresett (S ) hatásábra. M-2.16 Rácsos konzol rúder hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján Határozzuk meg a fels pályás rácsos konzol jelölt rúder hatásábráit szerkesztéssel! a) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S1 ) hatásábráját szerkesztéssel, a virtuális Az ( S1 ) hatásábrához a rúd átvágása a rácsos konzolt két merev tárcsából álló egyszabadságfokú láncolattá alakítja át. A II tárcsa mereven kapcsolódik a
falhoz, ezért nem mozdul el, tehát képe a nullvonal. Az (1) abszolút pólus az (1,2) relatív pólussal egybeesik A rúdban beiktatásra kerül egységnyi pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük a II tárcsa képét, azaz a nullvonalat, és az (1,2) pólusban elfordítjuk az I. tárcsát 12 = 4 / 3b szöggel úgy, hogy a rúdban egységnyi nyúlás keletkezzen. Ezzel kész a keresett ( S1 ) hatásábra 24 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.16a ábra b) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S 2 ) hatásábráját szerkesztéssel, a virtuális 2.16b ábra Az ( S 2 ) hatásábrához a rúd átvágása a rácsos konzolt ugyancsak két merev tárcsából álló egy-szabadságfokú láncolattá alakítja át. A II tárcsa most is mereven kapcsolódik a falhoz, nem mozdul el, tehát képe
a nullvonal. Az (1) abszolút pólus az (1,2) relatív pólussal egybeesik. A rúdban beiktatásra kerül egységnyik pozitív relatív eltolódást az (1,2) pólusban alkalmazott relatív elfordulás közvetítésével visszük be. Tetsz legesen felvesszük a II tárcsa 25 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján képét, azaz a nullvonalat, és az (1,2) pólusban elfordítjuk az I. tárcsát 12 = 1 / k szöggel úgy, hogy a rúdban egységnyi nyúlás keletkezzen. Ezzel kész a keresett ( S1 ) hatásábra c) Határozzuk meg a rácsos konzol elmozdulások tétele alapján ( S 3 ) hatásábráját szerkesztéssel, a virtuális 2.16c ábra Az ( S 3 ) hatásábrához a rúd átvágása a rácsos konzolt négy merev tárcsából álló egyszabadságfokú láncolattá alakítja át. Most a IV tárcsa kapcsolódik mereven a falhoz, tehát képe a nullvonal. Az egyes tárcsákat összekapcsoló csuklók alkotják az (1,2),
(1,3), (2,4) és (3,4) relatív pólusokat. Most is a megfelel tárcsák relatív elfordítása közvetítésével iktatjuk be az átvágott rúd két vége között az egységnyi pozitív relatív eltolódást: vagy az (1,3), vagy a (2,4) pólusban. Vegyük fel tetsz legesen az IV tárcsa képét, vagyis a nullvonalat, és fordítsuk el hozzá képest a II. tárcsát a 12 = 1 / k értékkel úgy, hogy a rúdban nyúlást okozzon. A hiányzó I tárcsa képét az (1,2) és (1,4) pólusok levetítésével szerkesztjük meg Az (1,4) pólust az (1,2), (2,4) (1,4) és az (1,3), (3,4) (1,4) összefüggésekb l a konzolvégen kapjuk meg, és a IV. tárcsa képére, a nullvonalra vetítjük le Ezáltal megkaptuk a keresett rúder hatásábrát. 26 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.17 Befogott Gerber-tartó igénybevételi és reakcióer hatásábrái szerkesztéssel, a virtuális elmozdulások tétele alapján (TK )
a) Határozzuk meg a Gerber-tartó jelölt keresztmetszetének hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! nyíróer 2.17a ábra A nyíróer nek megfelel görg s kapcsolat révén a tartó három tárcsából álló egyszabadságfokú láncolattá alakul. Mivel az I tárcsa mereven befogott, így nem mozdul el, minden pontja abszolút pólus. Ezért az I tárcsa képe a nullvonal, és az (1,2) relatív pólus egyben a (2) abszolút pólus is. A II és III tárcsát párhuzamosan eltoljuk egymáshoz képest egységnyivel, majd levetítjük a (2) és (3) pólusokat, és berajzoljuk a nullvonalat. Ezáltal megkaptuk a keresett hatásábrát. b) Határozzuk meg a Gerber-tartó K keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.17b ábra 27 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A keresztmetszetnél csuklót
teszünk be, ekkor a tartó ismét három tárcsából álló egyszabadságfokú láncolattá alakul, ahol a mozdulatlan befogott I. tárcsa képe ismét nullvonal Szabadon felvesszük vagy a II., vagy a III tárcsa képét, majd beiktatjuk a 23 = 1 relatív elfordulást a nyomatéki el jelszabály szerint pozitív el jellel. Ezután levetítjük a (2), illetve (3) abszolút pólusokat a megfelel tárcsák képére, és berajzoljuk a nullvonalat. Ezzel el állítottuk az ( M K ) hatásábrát. c) Határozzuk meg a Gerber-tartó A támaszánál keletkez reakcióer hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! (A) 2.17c ábra A reakcióer nek megfelel en eltávolítjuk a megtámasztást, hogy az abszolút eltolódást beiktathassuk. Ekkor a tartó két tárcsából álló egy-szabadságfokú láncolattá alakul, ahol ismét az I. tárcsa képe a nullvonal Ehhez képest vesszük fel a II tárcsa képét úgy, hogy a pozitív reakcióer vel
ellentétesen, lefelé mutató egységnyi eltolódás keletkezzen a támsz helyén. Így megkapjuk az (A) hatásábrát. d) Határozzuk meg a Gerber-tartó befogott tartórészén lév keresztmetszetének ( M K ) hajlítónyomatéki hatásábráját szerkesztéssel, a virtuális elmozdulások tétele alapján! 2.17d ábra 28 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján A keresztmetszetnél csuklót teszünk be, ekkor a tartó ismét három tárcsából álló egyszabadságfokú láncolattá alakul, ahol a mozdulatlan befogott I. tárcsa képe ismét a nullvonal, és az (1,2) relatív pólus egyben a (2) abszolút pólus is. E pontban forgatjuk el a II tárcsát az I.-hez képest egységnyi szöggel, majd a III tárcsa képét a (2,3) és (3) pólusok levetítése útján kapjuk meg. Ezzel el állítottuk az ( M K ) hatásábrát 2.2 Statikailag határozott tartók elmozdulási hatásfüggvényei a virtuális er k tétele
alapján A virtuális er k tételét a Rugalmasságtan tárgy keretében tárgyaltuk. A tétel ismertetése az alkalmazásokkal együtt a Szilárdságtan tankönyvben [4] található. A virtuális er$k tétele szerint egy elmozdulásrendszer akkor és csak akkor geometriailag lehetséges (kompatibilis), ha bármely virtuális er$rendszeren végzett (kiegészít$) munkája zérus. Elmozdulási hatásábrák készítésekor a mozgó egységer és az általa okozott, kompatibilis elmozdulás- és alakváltozás-rendszer változását vizsgáljuk. A tétel értelmében az egységer következtében fellép elmozdulások és alakváltozások tetsz leges virtuális er rendszeren végzett kiegészít munkájának összege az egységer minden helyzetében zérus. A virtuális kiegészít munka felírásához a tartón tetsz leges virtuális er rendszert kell felvenni. A virtuális er rendszer alapvet tulajdonsága, hogy egyensúlyi, azaz statikailag lehetséges, vagyis elemei a statikai
egyenletek által megszabott összefüggésben állnak egymással. Ezt az er rendszert tehát úgy kell felvennünk, hogy a vizsgált elmozdulási hatáson feltétlenül munkát tudjon végezni, ugyanakkor elégítse ki a tartón érvényes egyensúlyi feltételeket, amelyek a tartó virtuális igénybevételeihez vezetnek. Ezek a virtuális igénybevételek pedig az egységer b l származó valódi alakváltozásokon (relatív elmozdulásokon) végeznek kiegészít munkát. A kétféle virtuális kiegészít munka összegének – mivel az elmozdulások és alakváltozások kompatibilisek – zérust kell adnia. A virtuális er k tételének ezen felírása alapján megkapjuk a vizsgált elmozdulásnak a mozgó egységer egy adott helyzetéhez tartozó értékét. Ahhoz, hogy a mozgó egységer minden helyzetéhez megkapjuk a vizsgált elmozdulás értékét, azaz az elmozdulás hatásfüggvényét, a virtuális er k tételének két speciális alakját, Betti és Maxwell ún.
felcserélhet ségi tételét kell alkalmaznunk. 2.21 Betti és Maxwell felcserélhet ségi tételei Betti tételének megértéséhez tekintsük az 2.6 ábrán látható rugalmas anyagú, kis elmozdulást végz tartót, amelyre külön a (P), majd külön a (Q) er rendszer m&ködik. Mindkét teherhez meghatározzuk az igénybevételeket és az elmozdulásokat is. A 26a és b ábrán a függ leges eltolódások ábráit t&ntettük fel. 29 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.6 ábra – Betti és Maxwell felcserélhet$ségi tétele Alkalmazzuk kétféleképpen a virtuális er k tételét: el ször a (P), majd a (Q) er rendszert tekintve virtuálisnak, míg a másikat, és az abból származó elmozdulásokat és alakváltozásokat valódinak. A (P) er rendszert tekintve virtuálisnak, a tétel a ~ ~ ~ ~ ~ W = Wk + Wb = Wk , P ,Q + Wb, P ,Q = 0 alakot ölti, míg a (Q) er rendszert tekintve virtuálisnak, a
tétel ~ ~ ~ ~ ~ W = Wk + Wb = Wk ,Q, P + Wb,Q, P = 0 alakját kapjuk, ahol az indexek sorrendjében a munka küls , illetve bels jellege, a munkát végz dinám (illetve a munkavégzés helye), végül a munkában részt vev elmozdulást okozó ~ ~ dinám jut kifejezésre. A Wb, P ,Q és a Wb,Q , P bels kiegészít munkák az integrálkifejezéseikben szerepl igénybevételi függvények szorzatának felcserélhet sége ~ ~ következtében megegyeznek egymással, azaz Wb, P ,Q = Wb,Q , P , következésképpen a küls kiegészít munkák is megegyeznek ~ ~ Wk , P ,Q = Wk ,Q , P . 30 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Eszerint a virtuális (P) er rendszernek a valódi (Q) er rendszerb l származó elmozdulásokon végzett küls kiegészít munkája megegyezik a virtuális (Q) er rendszernek a valódi (P) er rendszerb l származó elmozdulásokon végzett küls kiegészít munkájával. Mivel pedig bármely tényleges
er rendszer virtuálisnak tekinthet , az állítás két valódi er rendszer esetére is igaz. Betti felcserélhet$ségi tétele szerint két dinámrendszer egymás hatására végzett küls$ idegen munkája egyenl$. Írjuk most fel Betti tételét az 2.6c ábrán látható tartóra, amikor a (P), illetve (Q) er rendszer egyetlen P, illetve Q er b l áll: P eP ,Q = Q eQ , P , ahol az els index a hely, a második az ok jelzésére szolgál. Ha mindkét er rendszer egységer kb l áll, azaz P = 1 és Q = 1 , akkor eP ,Q = eQ , P , vagyis a két elmozdulás felcserélhet . Maxwell felcserélhet$ségi tétele szerint két egységdinám által egymás támadáspontján okozott munka-kompatibilis elmozduláskomponensek felcserélhet$k. Más szóval megfogalmazva: két egységdinám esetén az elmozdulás helye és oka felcserélhet . Természetesen Betti és Maxwell tételei érvényesek bármilyen irányú er k és er párok esetén. Elmozdulási hatásábra készítésekor azonban az egyik
er a tartón mozgó – a gravitációs terheket képvisel – függ leges egységer . 2.22 Elmozdulási hatásfüggvények Az elmozdulási hatásfüggvények és hatásábrák készítése munkatételekre, Betti és Maxwell tételeire épül. 2.7 ábra – Elmozdulási hatásábrák 31 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Legyen a tartón mozgó egységer jele F = 1 , helyzetének koordinátája x . Jelölje C a helyen rögzített keresztmetszethez tartozó azon elmozdulást, amelynek (C ) hatásfüggvényét keressük (2.7 ábra) Mivel a C elmozdulást az F er okozza, a „hely-ok” index-sorrend értelmében C = C ,F . Iktassunk be a keresztmetszetben a vizsgált elmozdulással munka-kompatibilis Q = 1 egységdinámot. Ez a terhel F egységer hatásvonalában v F ,Q eltolódást okoz. A végzett küls munkák egyenl sége szerint F v F ,Q = Q C , F . Mivel F = 1 és Q = 1 , C , F = v F ,Q , azaz Maxwell
felcserélhet ségi tétele értelmében: A tartón mozgó egységer$ által okozott keresztmetszeti elmozdulás és a keresztmetszetben beiktatott, az elmozdulással munka-kompatibilis egységdinám által okozott eltolódás az egységer$ hatásvonalában felcserélhet$. A tétel az egységer helyzetét l függetlenül igaz. Mivel tehát az egységer mozog a tartón, és így a Q egységdinám által okozott vF ,Q = vQ=1 ( x) eltolódásfüggvénynek mindig más-más ordinátája fölé kerül, ezért (C ) = vQ=1 ( x) , vagyis a keresett elmozdulási hatásábra megegyezik a beiktatott egységdinám-okozta eltolódási ábrával. Eszerint: Az elmozdulási hatásfüggvény a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú egységdinámból kapott egységteher-irányú eltolódásfüggvénnyel azonos. Mivel a tartón mozgó egységer általában függ leges, az elmozdulási hatásábrakészítés egy függ leges eltolódási ábra
készítésére egyszer&södik. A statikailag határozott és határozatlan tartók elmozdulási hatásfüggvényeinek az el állítása azonos elvek alapján történik, azonban a beiktatott egységdinám hatására készítend függ leges eltolódási ábra meghatározása a statikailag határozatlan tartók esetén a tartó teljes vizsgálatát igényli. Ezért az alábbiakban csak a statikailag határozott tartók esetével foglalkozunk, és a határozatlan tartókra vonatkozó elmozdulási hatásábrákra a statikailag határozatlan tartók megoldásával foglalkozó fejezetekben térünk ki. 2.23 Abszolút és relatív elmozdulások hatásfüggvényei Abszolút eltolódás, illetve elfordulás hatásábráihoz a beiktatott egységdinám az elmozdulás pozitív el jelének megfelel er , illetve er pár. Abszolút elmozdulás hatásábrája a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú egységdinámból kapott függ$leges
eltolódási ábra. 32 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján Relatív eltolódás, illetve elfordulás hatásábráihoz a beiktatott egységdinám az elmozdulás pozitív el jelének megfelel kett s er , illetve kett s er pár. A relatív elmozdulás értelmezése szerint a viszonyítási pontok lehetnek távol is egymástól, de egybe is eshetnek. A beiktatott kett s egységdinámoknak a munka-kompatibilitás miatt a viszonyítási pontokat követniük kell. Relatív elmozdulás hatásábrája a keresztmetszetben beiktatott, az elmozdulással munkakompatibilis, azzal egyez$ irányú kett$s egységdinámból kapott függ$leges eltolódási ábra. Elmozdulási hatásábra esetén tehát az egységdinámot az elmozdulás pozitív irányával megegyez en kell felvenni, hogy el jelhelyes hatásábrát kapjunk. Az egyes elmozdulás-fajtáknak megfelel en beiktatandó egységdinámokat az alábbi táblázatban foglaljuk
össze. Hatásfüggvény, hatásábra abszolút eltolódás Jele A beiktatott alakváltozás (relatív elmozdulás) egységnyi koncentrált er az eltolódás irányában relatív eltolódás (eK ) ( K) (u jk ) két ellentett egységnyi koncentrált er az eltolódás irányában relatív elfordulás ( ij ) két ellentett egységnyi koncentrált er pár az elfordulás irányában abszolút elfordulás 2.24 egységnyi koncentrált er pár az elfordulás irányában Mintapéldák: Elmozdulási hatásábrák a virtuális er k tétele alapján Amint láttuk, a hatásábra-készítés a beiktatott egységdinámból származó függ leges eltolódási ábra elkészítéséb l áll. Statikailag határozott és határozatlan tartók elmozdulási hatásábrái egyaránt görbe vonalú ábrák, hiszen a tartó rugalmas vonalával azonosak. Ennek függvényét, az elmozdulási hatásfüggvényt megadni meglehet sen körülményes, hiszen az a rugalmas vonal differenciálegyenletének
megoldását igényelné. Kézi számítások céljára tehát csak a hatásábrát szokták elkészíteni, a függvény felírása nélkül, a függvény meghatározott ordinátáinak a kiszámításával. Az abszolút és relatív eltolódások és elfordulások hatásábráinak számítással történ meghatározása lépéseit az alábbi táblázatban foglaljuk össze. Az elmozdulási hatásábra-számítás lépései 1. 2. Beiktatjuk az elmozdulással munka-kompatibilis egységdinámot a pozitív elmozdulással megegyez en. Meghatározzuk a tartó függ leges eltolódási ábráját, magát a hatásábrát. Ennek módjai lehetnek: a. Eltolódási ábra a Szilárdságtanban tanult nyomatéki teher módszerével: a nyomatéki ábra el állítása után a szükséges támaszelfordulások meghatározása, a közbens (nyomatéki ábra-területekkel arányos) relatív elfordulások meghatározása, az eltolódási ábra el írt ordinátáinak kiszámítása. b. Eltolódási ábra a
Rugalmasságtanban tanult virtuális er k tétele alapján munkatétellel: a hatásábra el írt ordinátáinak közvetlen kiszámítása mindenegyes ordinátára külön alkalmazott munkatétellel. c. Eltolódási ábra kombinált módszerrel: a szükséges támaszelfordulások meghatározása munkatétellel, majd az el írt ordináták számítása a nyomatéki teher módszerével. 33 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján M-2.21 Kéttámaszú tartó elmozdulási hatásábrái a) Határozzuk meg a kéttámaszú tartó K keresztmetszetének (eK ) függ leges eltolódási hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . 2.21a ábra A keresztmetszetben beiktatunk egy olyan QK er t, amely a kérdéses eltolódáson munkát tud végezni. A Maxwell-féle felcserélhet ségi tétel értelmében ugyanis ennek a QK er nek a mozgó egységer által okozott, folytonosan változó érték&
keresztmetszeti eltolódáson végzett munkája megegyezik a mozgó egységer nek - bármely helyzetében - a QK er által okozott eltolódásokon végzett munkájával: QK eFK ( x) = F e y ,QK ( x) , ahol eFK ( x) = (eK ) . Mivel QK = 1 és F = 1 , így (eK ) = e y ,QK ( x) , vagyis a keresett eltolódási hatásábra a QK = 1 er hatására keletkez függ leges eltolódási ábrával egyenl . A hatásábra, azaz a függ leges eltolódási ábra görbevonalú. Ezért csak az el re kijelölt keresztmetszetekhez tartozó ordinátáit számítjuk ki, és ennek alapján közelít leg rajzoljuk meg a hatásábrát. A kijelölt ordinátákat valamely tanult módszer szerint számítjuk ki A nyomatéki teher módszere szerint a QK = 1 er b l megrajzolt nyomatéki ábra alapján elegend a B támaszelfordulást kiszámítani, majd a B támasztól kiindulva a keresett eltolódások számíthatók. Az e Ay = 0 feltételb l nagyított értékben B = 2,5 m 2 adódik, amelyb l az (eK ) hatásábra
ordinátáira az alábbi táblázat szerinti értékeket kapjuk: i (eK ) i nagyított [m 3 ] (eK ) i valódi [m / kN ] 0 6,0 10 3 A 1 2,5 6 4,5 2 = 0 6,0 2 2,5 4 2,0 1,333 = 7,33 7,33 10 3 3 2,5 2 0,5 0,667 = 4,67 4,67 10 3 0 B 34 (eK ) i számítása 0 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján b) Határozzuk meg a kéttámaszú tartó K keresztmetszetének hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . ( K ) elfordulási 2.21b ábra A keresztmetszetben beiktatunk egy olyan M K er párt, amely a kérdéses elforduláson munkát tud végezni. A Maxwell-féle felcserélhet ségi tétel értelmében ugyanis ennek az M K er párnak a mozgó egységer által okozott, folytonosan változó érték& keresztmetszeti elforduláson végzett munkája megegyezik a mozgó egységer nek - bármely helyzetében - az M K er pár által okozott eltolódásokon végzett munkájával: M K
FK ( x) = F e y ,M K ( x) , ahol FK ( x) = ( K ) . Mivel QK = 1 és F = 1 , így ( K ) = e y ,M K ( x) , vagyis a keresett elfordulási hatásábra az M K = 1 er pár hatására keletkez függ leges eltolódási ábrával egyenl . A görbevonalú hatásábra ordinátáit az el re kijelölt keresztmetszeteknél számítjuk ki, és ennek alapján rajzoljuk meg a hatásábrát. A kijelölt ordinátákat valamely tanult módszer szerint számítjuk ki. A nyomatéki teher módszere szerint az M K = 1 er párból megrajzolt nyomatéki ábra alapján elegend a B támaszelfordulást kiszámítani, abból kiindulva a keresett eltolódások számíthatók. Az e Ay = 0 feltételb l nagyított értékben B = 1,083 m 2 adódik, amelyb l az ( K ) hatásábra ordinátáira az alábbi táblázat szerinti értékeket kapjuk: i ( K ) i számítása ( K ) i nagyított [m 2 ] ( K ) i valódi [radián / kN ] A 1 1,083 6 2,25 2 = 0 2,0 0 2,0 10 3 2 1,083 4 1,0 1,333 = 3,0 3,0 10 3 3 1,083 2
0,25 0,667 = 2,0 2,0 10 3 0 B 0 35 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján c) Határozzuk meg a kéttámaszú tartó B támasz-keresztmetszetének hatásábráját! A tartó hajlítási merevsége állandó: EI = 10 3 kNm 2 . ( B ) elfordulási 2.21c ábra Mint tudjuk, a keresett elfordulási hatásábra a támasz-keresztmetszetben beiktatott M B = 1 er pár hatására keletkez függ leges eltolódási ábrával egyenl . A görbe vonalú hatásábra ordinátáit most is az el re kijelölt keresztmetszeteknél számítjuk ki, és ennek alapján rajzoljuk meg a hatásábrát. A nyomatéki teher módszere szerint az M B = 1 er párból megrajzolt nyomatéki ábra alapján most a A támaszelfordulást kiszámítjuk ki, majd az A támasztól kiindulva nyerjük a keresett eltolódásokat. Az eBy = 0 feltételb l nagyított értékben A = 1,333 m 2 adódik, amelyb l az ( B ) hatásábra ordinátáira az alábbi táblázat
szerinti értékeket kapjuk: ( B ) i számítása ( B ) i nagyított [m 2 ] ( B ) i valódi [radián / kN ] A 1 1,333 2 + 0,25 0,667 = 0 2,5 0 2,5 10 3 2 1,333 4 + 1,0 1,333 = 4,0 4,0 10 3 3 1,333 6 + 2,25 2 = 4,5 4,5 10 3 0 i B 0 M-2.22 Összetett tartó elmozdulási hatásábrái a) Határozzuk meg az összetett tartó K keresztmetszetének (eKy ) függ leges eltolódási hatásábráját! A tartó hajlítási merevsége a csuklótól balra EI1 = 10 4 kNm 2 , a csuklótól jobbra pedig EI 2 = 1,5 10 4 kNm 2 . A két támasztórúd húzó-nyomó merevsége megegyezik: EA1 = EA2 = 4 10 4 kN . 36 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása munkatételek alapján 2.22 ábra Legyenek az alapul választott merevségek az alábbiak: EI 0 = EI1 = 10 4 kNm 2 , EI 2 = 1,5 EI 0 , továbbá EA0 = EA1 = EA2 = 4 10 4 kN . Eszerint i02 = EI 0 / EA0 = 0,25 m 2 37 Tartók statikája 2. Er - és elmozdulási hatásábrák összefoglalása
munkatételek alapján A Maxwell-féle felcserélhet ségi tétel értelmében a keresett eltolódási hatásábra a mozgó egységer által érintett tartószakasz, a „pálya” QKy = 1 er hatására keletkez függ leges eltolódási ábrájával egyenl . Ennél az összetett szerkezetnél a függ leges eltolódási ábra meghatározása nem túl egyszer&. A feladatnak többféle megoldási menete lehetséges, itt az alábbi eljárást követjük: meghatározzuk az A támasznál keletkez A abszolút, és a C csuklónál keletkez C relatív elfordulást, majd az A támasztól kiindulva számítjuk ki a pálya jelölt keresztmetszeteiben a függ leges eltolódásokat. Az elmozdulások számítására a Szilárdságtanban és a Rugalmasságtanban tanult módszereket alkalmazzuk. Most például a A támaszelfordulás meghatározására munkatételt választunk, majd annak ismeretében a C relatív elfordulást a nyomatéki teher módszerével határozzuk meg. A b) ábrán
felrajzoltuk a QKy = 1 er b l keletkez nyomatéki ábrát. Látjuk, hogy ekkor a támasztórudakban – kivételesen – nem ébrednek er k. Mivel a A támaszelfordulást munkatétellel határozzuk meg, az A támasznál beiktatunk egy M A = 1 virtuális nyomatékot, amelyhez tartozó nyomatéki ábrát és rúder ket a c) ábra mutatja. A támaszelfordulás értéke: Si Si M M 3 3 2 ds + i02 si = 0,5 = 2,121 m 2 ( ), A = ( s) 2 1 , 5 i amelyben a rúder knek nem volt szerepe. A A támaszelfordulás ismeretében az A támasztól a B támaszig terjed zárt vonalon a C relatív elfordulást abból a feltételb l számítjuk ki, hogy a B támasz az S1 rúd irányában nem mozdul el. A d) ábra értelmében: 12 8 3 = 0 , azaz 2,121 12 4,243 8 C 3 = 0 A 1 C 2 2 2 amelyb l C = 2,831 m 2 . Ezek után az (eKy ) hatásábra jelölt keresztmetszetekhez tartozó ordinátáit az A támasztól kiindulva az alábbi táblázat szerint kapjuk: i (eKy ) i számítása (eKy ) i nagyított [m 3 ] (eKy
) i valódi [mm / kN ] 1 2 3 4 5 6 2,121 0 + 4,243 2 + 3,0 2 = 2,121 3 4,243 1 = 2,121 6 4,243 4 = 2,121 9 4,243 7 + 2,831 3 = 2,121 12 4,243 10 + 2,831 6 = 2,121 15 4,243 13 + 2,831 9 = 14,486 2,120 -4,246 -2,119 0 2,135 1,4486 0,2120 -0,4246 -0,2119 0 0,2135 Megjegyezzük, hogy ugyanezt az eredményt többféle úton is megkaphatjuk. Például úgy, hogy a C relatív elfordulást is munkatétellel határozzuk meg, majd utána az eddigiekhez hasonlóan számítjuk ki a hatásábra ordinátáit. Teljesen eltér megoldási út, ha a hatásábra valamennyi ordinátáját külön-külön alkalmazott munkatétellel határozzuk meg. A tanulság ebb l az, hogy minden feladat más-más megoldási stratégiát igényel, amelynek kiválasztását a számítási munka egyszer&ségére való törekvés vezérli. 38




 When reading, most of us just let a story wash over us, getting lost in the world of the book rather than paying attention to the individual elements of the plot or writing. However, in English class, our teachers ask us to look at the mechanics of the writing.
When reading, most of us just let a story wash over us, getting lost in the world of the book rather than paying attention to the individual elements of the plot or writing. However, in English class, our teachers ask us to look at the mechanics of the writing.