Architecture | Earthworks » Földművek jegyzet

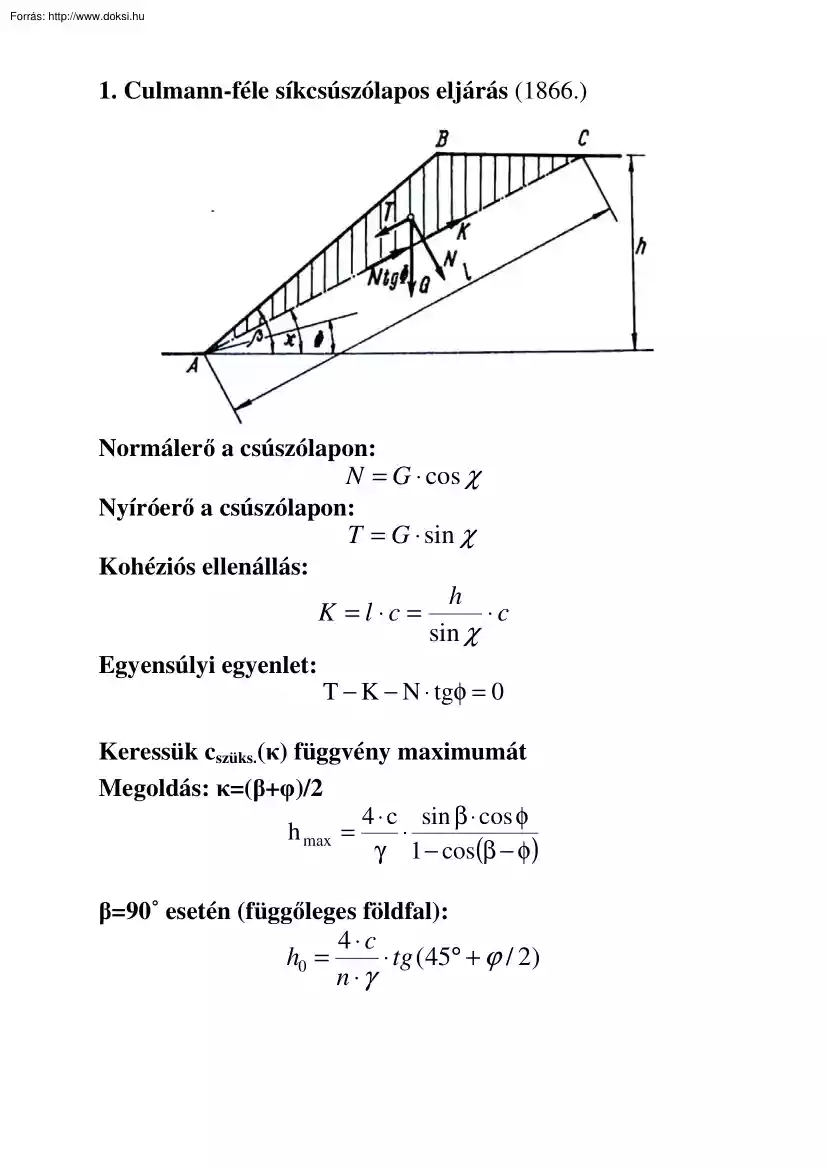
1. Culmann-féle síkcsúszólapos eljárás (1866) Normálerő a csúszólapon: N = G ⋅ cos χ Nyíróerő a csúszólapon: T = G ⋅ sin χ Kohéziós ellenállás: K = l ⋅c = h ⋅c sin χ Egyensúlyi egyenlet: T − K − N ⋅ tgφ = 0 Keressük cszüks.(κ) függvény maximumát Megoldás: κ=(β+φ)/2 4 ⋅ c sin β ⋅ cos φ h max = ⋅ γ 1 − cos(β − φ) β=90˚ esetén (függőleges földfal): h0 = 4⋅c ⋅ tg (45° + ϕ / 2) n ⋅γ 2. Svéd nyomatéki módszer (c>0, φ=0) l z = r⋅ i lh K=c⋅lh K⋅z=G⋅a l c ⋅ lh ⋅ r ⋅ i = G ⋅ a lh csz = G⋅a r ⋅ li n= ct csz 3. Szőnyegcsúszás elmélete (c=0, φ>0) c=0 ν = Középső főfeszültség hatása: tgφ . tgε 4. Bishop-módszer Csúszólap lamellákra osztása Feltétel: globális erőegyensúly (zárt vektorpoligon) Biztonsági tényező értelmezése (a nyírószilárdságban): tgφn = Megoldás: iterációval tgφ νn , cn = c νn 5. Egyszerűsített

Bishop-módszer (HF) Vizsgálat helye: legmagasabb töltésben Feltételezés: Eb i = E j i K i = c ⋅ Li i S i = N i ⋅ tgϕ E ji E bi N i = Gi ⋅ cos α i Ni Ti = Gi ⋅ sin α i Gi Ti Ki Si i ν= r ⋅ Σ ( Sϕ i + K i ) r ⋅ ΣTi = Σ(c ⋅ Li + tgφ ⋅ Gi cos α i ) ΣGi sin α i Felosztás: 8-10 db lamella, sorszámmal Csúszólap: 3 különböző (szelvényszám, magasság, rézsűszög) b c a 6. Taylor-módszer (grafikon) β φ N c C szükséges=NC·h·γ Mintapélda: h=10 m γ= 20 kN/m3 β=30˚ φtényleges=17˚ ctényleges=16 kPa φ [˚] 0 tg φ 0 NC 5 10 15 20 25 0,087 0,176 0,268 0,364 0,466 0,155 0,112 0,075 0,049 0,025 0,01 cszüks. [kPa] 31,0 22,4 15,0 9,8 5,0 2,0 Összetett biztonság 35 kohézió (kPa) 30 25 20 A 15 υ= B 10 5 0 0 0,1 0,2 0,3 tg f 0,4 0,5 OA = 1,34. OB 7. Blokk-módszer (tömbcsúszás) -HF Vizsgálat helye: legmagasabb bevágásban 1 H/n1 Ea N H 2 S H/n2 csl G T K L Ea:

aktív Rankine-állapot N = G ⋅ cos α S = N ⋅ tgϕ csl . T = G ⋅ sin α K = L ⋅ ccsl . S+K n= T + Ea 8. Véges elemes módszer φ-c redukció: c + σ ⋅ tg φ c r + σ ⋅ tg φ r ΣMsf: redukciós tényező n=max.(ΣMsf) n=