Kémia | Felsőoktatás » A makro világa, második fejezet

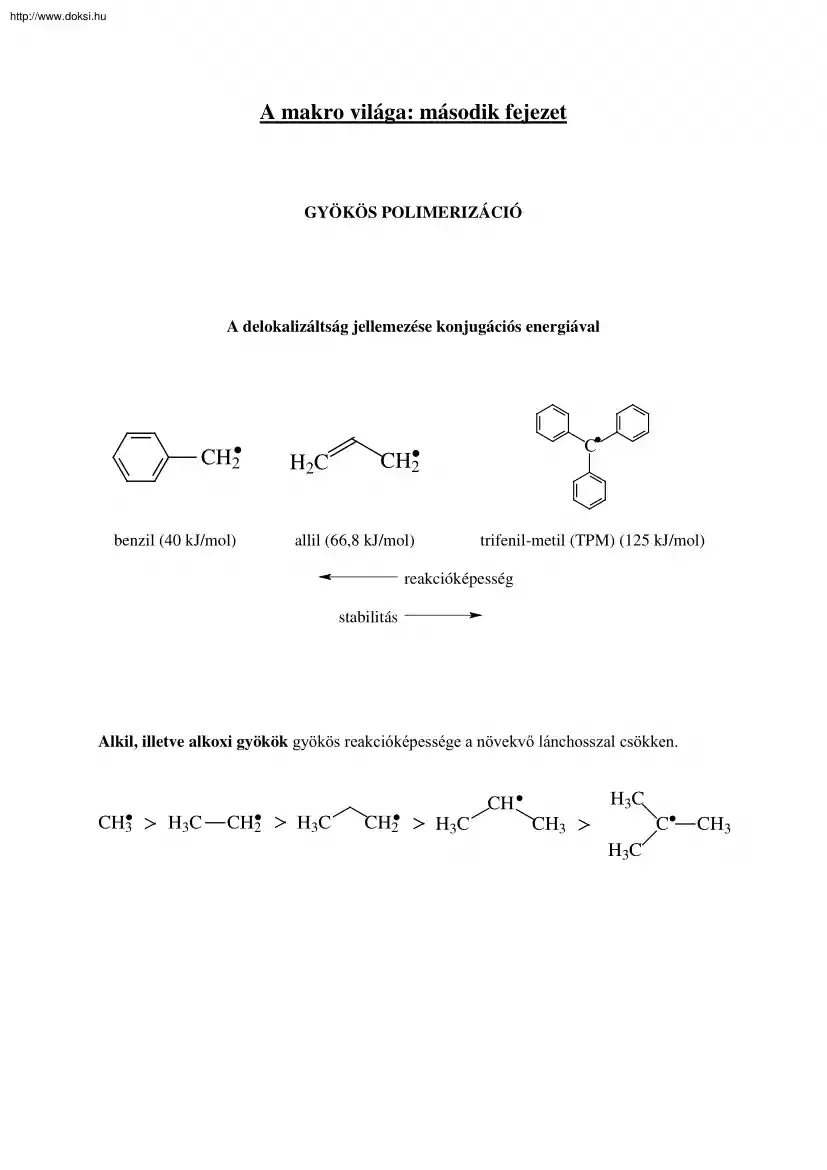
http://www.doksihu A makro világa: második fejezet GYÖKÖS POLIMERIZÁCIÓ A delokalizáltság jellemezése konjugációs energiával CH2 benzil (40 kJ/mol) H2C C CH2 allil (66,8 kJ/mol) trifenil-metil (TPM) (125 kJ/mol) reakcióképesség stabilitás Alkil, illetve alkoxi gyökök gyökös reakcióképessége a növekvő lánchosszal csökken. H 3C CH CH3 H3C CH2 H3C CH2 H 3C C CH3 H 3C CH3 http://www.doksihu GYÖKÖS POLIMERIZÁCIÓ Stabilis szabad gyökök: TPM (trifenil-metil gyök): . C DPPH: . NO2 N N NO2 NO2 Banfield gyök: CH3 CH3 CH3 . C CH2 C N O N O GYÖKÖS POLIMERIZÁCIÓ http://www.doksihu Egy szabad gyök legfontosabb reakciói a következők: - addíció telítetlen kötésre (propagáció, láncátadás, inhibició), - szubsztitúció (láncátadás, inhibició), - reakció másik szabad gyökkel (lánczáródás), - bomlási reakció (depolimerizáció), - izomerizáció (dezaktiválódás átrendezéssel).

A szabad gyökök élettartama az eltűnéshez vezető reakciók sebességi állandójával fordítva arányos. τ≈ 1 ≈ 10 −6 − 10 −10 [s] k http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ ELEMI LÉPÉSEI 1. Iniciálás (initiation): I R• ki 2. Láncnövekedés (chain propagation): R• + M P1• k p1 P1• + M P2• kp2  Pi • + M Pi +•1 k pi 3. Lánczáródás (chain termination): Pi + j Pi + Pj kt ,r kt ,d Pi • + X Pi + X • ktr • • Pi + Pj 4. Láncátadás (chain transfer): 5. Inhibíció, retardálás (inhibition, retardation): • Pi + Z Ahol Pi + Z • Pi Z • kinh I , M , X, Z, Pi : iniciátor, monomer, láncátadószer, inhibitor (retarder), polimer molekula, R• , Pi • , X • , Z • : szabad gyökök. http://www.doksihu Molekulatömeg v áltozás Molekulatömeg v áltozás Molekulatömeg v áltozás A MOLEKULATÖMEG VÁLTOZÁSA AZ ÁTALAKULÁSSAL 0 20 40 60 Konv erzió (%) a., 80 100 0 20 40 60

Konv erzió (%) b., 80 100 0 20 40 60 Konv erzió (%) c., a. Polimerizációs láncreakció; b. Lépéses polimerizáció; c. Meghatározatlan ionos polimerizációs láncreakció és protein szintézis (élőpolimerizáció) 80 100 http://www.doksihu GYÖKÖS INICIÁLÁS Az iniciátor bomlás lehet termikus vagy fotokémiai: I 2 fR• kb A bomlás sebessége: − dI = kb I dt A gyökképződés sebessége: dR • = 2 k b fI dt Maga az iniciálás gyors: R• + M P1• (= RM • ) A sebesség-meghatározó lépés a lassú iniciátorbomlás: dR• = ki I vi = dt ( ki = 2 kb f ) f az ún. gyökhasznosítási tényező: a képződő gyököknek az a hányada, amely rekombináció nélkül kijön az oldószer kalitkából (kalitka-effektus.) Az f definíciójából következik, hogy f ≤ 1. PEROXI-TÍPUSÚ INICIÁTOROK http://www.doksihu Hidroperoxidok: bomlási hőmérséklet 100-150oC t-Butil-hidroperoxid: CH3 CH3 C CH3 O OH CH3 CH3 C . O +

OH CH3 O CH3 C . CH3 + CH3 Kumil-hidroperoxid: CH3 C CH3 CH3 O OH C . O + OH CH3 CH3 C . O + CH3 http://www.doksihu PEROXI-TÍPUSÚ INICIÁTOROK Dialkil és diaril peroxidok: bomlási hőmérséklet 100 °C felett. Dibenzoil-peroxid: O C O O O C . O 2 C O . + CO2 CCl 4 -oldószerben 96 % CO 2 keletkezik. Mozgékony (reaktív) hidrogén atomot tartalmazó közegben a következő folyamat játszódik le: O C . O + RH O C . +R OH benzoesav http://www.doksihu PEROXI-TÍPUSÚ INICIÁTOROK Fontos peroxidok még a di-t-butil-peroxid és a di-kumil-peroxid. CH3 CH3 C CH3 O O CH3 C CH3 CH3 2 CH3 C CH3 O CH3 di-t-butil-peroxid O CH3 CH3 C CH3 C CH3 CH3 O O C CH3 + CH3 C 2 O CH3 CH3 di-kumil-peroxid O C CH3 + CH3 http://www.doksihu PEROXI-TÍPUSÚ INICIÁTOROK Peroxi-dikarbonátok: bomlási hőmérséklet 30 °C körül. RO C C O O O OR 2 RO + 2 CO2 O R: etil, izopropil, stb. Vizes közegben (emulziós

polimerizációhoz) használható iniciátorok a következők: Hidrogén peroxid: H 2 O 2 2 • OH ( ) Perszulfátok K ⊕ , NH ⊕ 4 : O K(O3S O O SO3)K 2 . O O S OK http://www.doksihu AZO INICIÁTOROK Az azo iniciátorokból nitrogénvesztés közben gyökök képződnek: R − N = N − R 2R • + N 2 Az egyik leggyakrabban alkalmazott gyökös iniciátor az azo-bisz-izo-butironitril (AIBN): 50 o C körül bomlik. CH3 CH3 C N N C CH3 2 CH3 C + N2 CN CN CN . CH3 CH3 (Primer rekombináció miatt f ≈ 0,6 - 0,8 ) DIAZO INICIÁTOROK Diazo-amino-benzol 100 oC körül: N N . NH + . NH + N2 Diazo-észter és diazo-tio-észter: O N N O C O R N N S C R http://www.doksihu NÉHÁNY INICIÁTOR FELEZÉSI IDEJE Felezési idő Iniciátor 50 oC 60 oC 70 oC 85 oC 100 oC 115 o C AIBN 74 h 4,8 h Benzoil-peroxid 130 145 oC o 155 o C C 176 o C 7,2 min 7,3 h 1,4 h 19,8 min Acetil-peroxid 158 h Lauril-peroxid 47,7 12,8 h h

Butil-peroxid 8,1 h 1,1 h 3,5 h 30 min 88 h 2,5 h 1,9 h 18 min Kumil-peroxid 13 h 1,7 h 16,8 min t-Butil-peroxid 218 h t-Butil-hidroperoxid 338 h 34 h 6,4 h 1,38 h 44,9 4,81 h h A felezési idők az iniciátorok benzolos vagy toluolos oldatára érvényesek. http://www.doksihu REDOX RENDSZEREK Az iniciálás olyan redox rendszerrel is végbemehet, ahol változó vegyértékű fém (Me) és karbonsav lép reakcióba: O R C O + OH- R C OH Men+ Me(n+1)+ O O R C R C OH + H+ O Termikus és fotoiniciálás iniciátor nélkül Sztirol termikus "öniniciálásának" valószínű mechanizmusa a következő: 2 CH2 CH . . CH CH2 CH2 CH http://www.doksihu Fotoiniciálás CCl 4 jelenlétében: CH2 CH hv CH2 CH X CCl4 Cl CH2 . CH + CCl3 X X REDOX RENDSZEREK Láncnövekedés k p1 ≈ k p 2 ≈ k p 3 =. = k pi = k p Legvalószínűbb a fej-láb kapcsolódás: . ~ CH2 CH + CH2 CH X X Diénpolimerizációnál allil-gyök képződik: kp

. ~ CH2 CH CH2 CH X X http://www.doksihu . R + CH2 CH CH CH2 R 1,2 R CH2 CH CH . CH2 CH CH CH2 CH2 1,4 R CH2 CH CH . CH2 http://www.doksihu REDOX RENDSZEREK Lánczáródás A lánczáródás történhet a gyökök rekombinációjával (pl. PS, PAN) i ~ CH2 . j i+j CH + CH CH2~ X k t,r ~ CH2 X CH CH CH2~ X X vagy diszproporcionálódással (pl. PVAc): i . j i ~ CH2 CH + CH CH2~ X k t,d j ~ CH CH + CH2 CH2~ X X X A diszproporcionálódás és a rekombináció sebességi állandóinak aránya: kt ,d kt ,r 40 oC 0,49 60 oC 0,75 80 oC 1,27 k t,d : a diszproporcionálódással történő termináció és k t,r : a rekombinációval történő termináció sebességi állandója. http://www.doksihu REDOX RENDSZEREK Láncátadás:  Oldószerre (HY): ~ CH2 . CH + HY k tr,s ~ CH2 . CH2 + Y X X A polimerizáció (a kinetikai lánc) megy tovább: Y• + M Y - M •  Monomerre: ~ CH2 . CH + CH2 CH X X . CH CH CH2 ~

CH2 X X ~ CH2 CH2 + CH2 X ~ CH . . C kp k tr, 1 X CH + CH3 CH X X k tr, 2 http://www.doksihu REDOX RENDSZEREK Vinil-acetát esetén például a következő folyamat játszódik le: ~ CH2 . CH + OC CH3 CH2 CH OC k tr, 3 ~ CH2 CH3 CH2 + CH2 CH OC OC O O O CH3 . CH2 O Láncátadó konstansok: CM = ktr , M kp Ahol k tr,M a sebességi állandó, k tr a láncátadás sebességi állandója és k p a láncnövekedés sebességi állandója. C M értékek néhány monomerre Monomer Akril-amid Akril-nitril Etilén Metil-akrilát Metil-metakrilát Sztirol Vinil-acetát Vinil-klorid C M x104 0,6-0,12b 0,26-0,3 0,4-4,2 0,036-0,325 0,07-0,25 0,30-0,60 1,75-2,8 10,8-16 Minden C M 60 oC-ra vonatkozik, a kivétel jelölve van b C M 40 oC-on http://www.doksihu REDOX RENDSZEREK Láncátadás  Polimerre: ~ CH2  . CH + ~ CH2 CH~ X X k tr, p CH2 + ~ CH2 . X X Iniciátorra: . ~ CH2 CH + R R k tr,i X  ~ CH2 . ~ CH2 CH R + R X

Inhibítorra: ~ CH2 . CH + HZ X k inh ~ CH2 . CH2 + Z X C~ http://www.doksihu INICIÁTOR LÁNCÁTADÓ KONSTANSOK (C I ) C I polimerizációjára Iniciátor 2,2 -Azo-bisz-butiro-nitril Sztirol 0,091-0,14 Metil-metakrilát 0,02 Akrilamid - 0,00076-0,00092 - - Kumil-peroxid (50 oC) 0,01 - - Lauroil-peroxid (70oC) 0,024 - - 0,048-0,10 0,02 - t-Butil-hidroperoxid 0,035 - - Kumil-hidroperoxid 0,063 0,33 - - - 0,0026 ′ t-Butil-peroxid Benzoil-peroxid Perszulfát (40 oC) C I értékek 60 oC-ra vonatkoznak, az ettől eltérő hőmérséklet jelölve van. A kinetikai lánchossz definíció szerint: Míg a polimerizáció fok: Pn = ν= propagáció valószínűsége termináció valószínűsége propagáció valószínűsége termináció + transzfer valószínűsége A kinetikai lánchossz és a polimerizáció fok között az összefüggés a következő: ν ≥ Pn http://www.doksihu ÁTADÓ KONSTANSOK LÁNCÁTADÓ ANYAGOKRA Átadó

anyag Benzol Ciklohexán Heptán Toluol Etil-benzol Izopropil-benzol t-Butil-benzol n-Butil-klorid n-Butil-bromid 2-Klór-bután Aceton Ecetsav n-Butanol Etil-éter Kloroform n-Butil-jodid Butil-amin Trietil-amin Di-n-butil-szulfid Di-n-butil-diszulfid Széntetraklorid Széntetrabromid n-Butil-merkaptán C s x104 Sztirol 0,023 0,031 0,42 0,125 0,67 0,82 0,06 0,04 0,06 1,2 4,1 2,0 1,6 5,6 3,4 1,85 7,0 7,1 22 24 110 22 000 210 000 Vinil-acetát 1,2 7,0 17,0 (50 oC) 21,6 55,2 89,9 3,6 10 50 11,7 1,1 20 45,3 150 800 370 260 10 000 10 700 390 000 480 000 A C s értékek 60 oC-ra vonatkoznak, az ettől eltérő hőmérséklet jelölve van. http://www.doksihu POLÁRIS HATÁSOK A LÁNCÁTADÁSBAN Láncátadó anyag Monomer CCl 4 (C 2 H 5 ) 3 N C s x104 k tr C s x104 k tr Vinil-acetát 10 700 2400 370 85 Akril-nitril 0,85 0,17 3800 760 1,25 (80 oC) 0,26 (80 oC) 400 84 Metil-metakrilát 2,4 0,12 1900 98 Sztirol 110 1,8 7,1 0,12 Metil-akrilát A C s

értékek 60 oC-ra vonatkoznak, az ettől eltérő hőmérséklet jelölve van. http://www.doksihu TELOMERIZÁCIÓ Telomerizáció: az a folyamat, amelyből a végcsoport (telos = vég) kialakítása láncátadással történik. Ennek lépései: - iniciálás (a primer gyök átalakítása A funkcióvá): R • + AB RB + A • - láncnövekedés A • + M AM •  AM n M • AM n +1 M • - láncátadás (a láncvég kialakítása B funkcióvá): AM n M • + AB A - M n +1 - B + A • Ipari példa az etilén polimerizációja széntetraklorid jelenlétében: R • + CCl 4 RCl + • CCl 3 • Cl 3C - (CH 2 - CH 2 )n - CH 2 - C H 2 + CCl 4 Cl 3C - (CH 2 - CH 2 )n +1 - Cl + • CCl 3 http://www.doksihu INHIBÍCIÓ, RETARDÁLÁS A folyamatok lejátszódhatnak - addíciós mechanizmus szerint: R • + Z RZ • vagy R • + Z • RZ - és szubsztitúciós mechanizmus szerint: R • + HZ RH + Z• Az inhibíciót az indukciós periódussal tudjuk jellemezni: t ind

= µ ⋅ Cinh vi ahol µ: sztöchimetriai koefficiens, melynek értéke elvileg 1 vagy 2, gyakorlatilag azonban 0 < µ ≤ 2; C inh inhibitor koncentrációja; v i : az inhibíció sebessége. http://www.doksihu INHIBÍCIÓ, RETARDÁLÁS Inhibitorok vagy retarderek lehetnek:  vegyérték telített molekulák: kinonok: . . RO . R+O O O . O R RO O R O . R R + HO R O OR O R R HO OR Aromás nitro-vegyületek: . O - R+ + N RO . Ar N Ar . R ROR + ArN O O O Kondenzált-gyűrűs aromás vegyületek: . R + R . CH R R R http://www.doksihu INHIBÍCIÓ, RETARDÁLÁS Inhibitorok vagy retarderek lehetnek:  Stabilizált szabad gyökök: 1. TPM, DPPH, Banfield-gyök (rekombináció játszódik le) 2. Az O 2 is szabad gyök (biradikális, iniciálni is tud!) 3. Változó vegyületű fémek, pl Fe A vas az egyik leggyakrabban használt szerkezeti anyag – jelenlétével és szennyezésével is gyakran számolni kell.

Autoinhibíció . ~ CH2 CH CH2 CH . láncnöv. CH2X CH2X ~ CH2 CH + CH2 CH CH2X CH2X izomerizáció ~ CH2 CH2 . CH X láncátadás ~ CH2 CH2 + CH2 CH CH2X . CHX http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ KINETIKÁJA A polimerizációs folyamat a következő: I 2R• kb R• + M P1• Pn• + M Pn•+1 kP Pi • + Pj• polimer kt Iniciátor bomlásra a sebességi egyenlet: − dI = kb I dt Gyökképződésre, iniciálásra az alábbi összefüggés írható fel: dR • = k i I = 2k b f I vi = dt f: gyökhasznosítási tényező. ν i : az iniciálás sebessége Propagációra, monomer-fogyásra: vp = − dm = kpr m dt (r = R + ∑ P ) • ν p : a láncnövekedés sebessége A gyökkoncentráció változása az előbbiek felhasználásával: dr = vi − k t r 2 dt • i http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ KINETIKÁJA A stacionárius állapot (steady state) miatt  dr dm  r nem konstans, de << dt dt  dr ≈0

dt vi = k t rst2 rst = vi = kt    2k b f ⋅ I kt A stacionárius gyökkoncentrációval a láncnövekedési folyamat sebessége: v p = k p rst m = k p  dI - Ha I = I 0 (= konstans),   dt << 2k b f kt dm dt I ⋅m = K I ⋅m   :  a propagáció sebessége: vp = − dm dm = K I0 ⋅ m = − K I 0 dt dt m a differenciál - egyenlet megoldása: ln m0 = K I0 ⋅ t m ahol K I 0 a polimerizáció bruttó sebességi állandója. http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ KINETIKÁJA - Ha I nem konstans, akkor − dI = k b I I = I 0 e − kb t dt behelyettesitve k t − b dm − = K I0 e 2 ⋅ m dt Ebből 2k I 0 m ln 0 = m kb k t − b   1 − e 2     ahol I o az iniciátor kezdeti koncentrációja. Az iniciátor elfogyása utáni határkonverzió („dead-end”) a következő: m0 2 K I 0 ln = m∞ kb http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ KINETIKÁJA A polimerizáció

sebessége (R p ) és az iniciátor koncentráció négyzetgyöke (I1/2) közötti összefüggés 24 22 20 Rp *106, (mol/l-sec) 18 16 14 12 10 8 6 4 2 0 0,00 0,05 0,10 0,15 0,20 0,25 1/2 [I] , (mol/l) ♦= Metil-metakrilát, benzoil-peroxid, 50 oC =Vinil-benzolát, azo-bisz-izo-butironitril, 60 oC 0,30 http://www.doksihu A GYÖKÖS POLIMERIZÁCIÓ KINETIKÁJA A polimerizáció aktiválási energiája: E = Ep + ahol: 1 E p − Et : 2 1 1 Eb − Et 2 2 a monomerre jellemző ≈15-25 kJ/mol. Eb : az iniciálás módjától, illetve az iniciátortól függ: termikus iniciálásnál ≈ 120-180 kJ/mol A kp kt redox-rendszernél ≈ 40-60 kJ/mol foto-iniciálásnál ≈ 0 kJ/mol. kifejezés értéke a monomertől függ: minél reakcióképesebb a monomerből képződött gyök, annál nagyobb kp kt . Például néhány monomerre a sorrend: VAc > VC > MMA > S (a monomerek reaktivitása fordított sorrendben változik) http://www.doksihu A

GYÖKÖK HOSSZÚSÁG SZERINTI ELOSZLÁSA A különböző gyökök koncentrációjának időbeli változása: dr1 = vi − k p r1 m − k t r1 r dt dr2 = k p r1 m − k p r2 m − k t r2 r dt  dri = k p ri −1 m − k p ri m − k t ri r dt dr ∑ : dt = νi − k t (r1 + r2 + . + ri )r = νi − k t r 2 ≈ 0 Rekurzió van, tehát ri = ahol kpm k p m + kt r ⋅ rr −1 = α ⋅ ri −1 α = a láncnövekedés valószínűsége, 1-α = a lánczáródás valószínűsége. Ennek alapján: r1 = νi k p m + kt r = kt r ⋅ r = (1 − α ) ⋅ r k p m + kt r tehát az eloszlás-függvény: ri = (1 − α )α i −1 r Ez geometriai eloszlás. http://www.doksihu A POLIMEREK HOSSZÚSÁG SZERINTI ELOSZLÁSA Diszproporcionálódás esetén a gyökök eloszlása „befagy”: NP = k t , d rP r = ∞ ∑k t ,d rP r rP = (1 − α )α P −1 r P= 1 ahol N p a P polimerizáció fokú részecskék száma. Ez az ún. legvalószínűbb („most probable”), vagy

„Flory”-eloszlás Rekombináció esetén: P −1 Np = ∑k ∞ ⋅ ri ⋅ rP −i t ,r i =1 P −1 ∑∑ k t ,r ⋅ ri ⋅ rP −i P = 2 i =1 P −1 ∑ (1 − α ) α 2 α P −i −1 = (1 − α ) i −1 P −1 2 i =1 ∑α P −2 = (1 − α ) (P − 1)α P −2 2 i =1 ∞ ∑ (1 − α ) (P − 1)α 2 P−2 = (1 − α ) ⋅ 2 P=2 1 =1 (1 − α )2 mert ∞ ∞ d x (α ) = d ∑ α x = dx x =1 P=2 x =1 x =1 dx d [α (1 + α + α 2 + .)] = d  α  = 1 − α + α2 = 1 2 = dα dα  1 − α  (1 − α ) (1 − α ) ∑ (P − 1)α P−2 ∞ ∞ = ∑ xα x −1 = ∑ Így N p = (1 − α ) (P − 1)α P −2 2