Matematika | Analízis » Differenciálhatóság

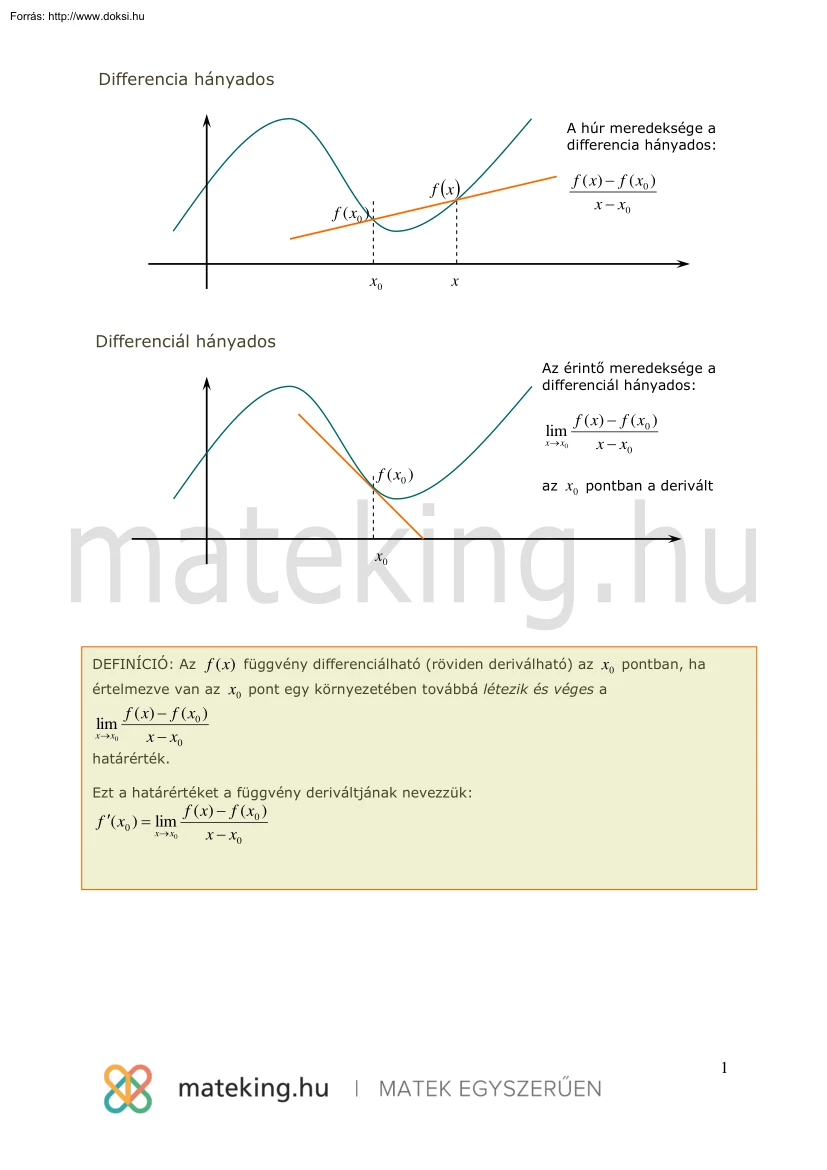
Differencia hányados A húr meredeksége a differencia hányados: f ( x )  f ( x0 ) x  x0 f x  f ( x0 ) x0 x Differenciál hányados Az érintő meredeksége a differenciál hányados: lim x x0 f ( x0 ) az f ( x )  f ( x0 ) x  x0 x0 pontban a derivált x0 DEFINÍCIÓ: Az f (x) függvény differenciálható (röviden deriválható) az x0 pontban, ha értelmezve van az lim x x0 x0 pont egy környezetében továbbá létezik és véges a f ( x )  f ( x0 ) x  x0 határérték. f ( x0 ) Ezt a határértéket a függvény deriváltjának nevezzük: f ( x0 )  lim x x0 f ( x )  f ( x0 ) x  x0 1 ALAPDERIVÁLTAK (c)  0 (sin x)  cos x (arcsin x)  ( x n )  n  x n1 (cos x)   sin x (arccos x)  1 1 x2 1 (e x )  e x 1 cos 2 x 1 (ctgx )  sin 2 x 1 x2 1 (arctgx )  1 x2 1 (arcctgx )  1  x2 (a x )  a x  ln a (shx) 

chx (arshx)  (chx)  shx (archx)  1 n 1 1 1 ( x )  ( x )   x n n n (ln x)  1 x (log a x)  1 1  x ln a (tgx )  (thx )  1 ch 2 x 1 x2 1 1 x 2 1 1 (arthx)  1  x2 DERIVÁLÁSI SZABÁLYOK Példák 1. (c  f )  c  f  (5  x 3 )  5  3x 2 f f 2.      x 5   5x 4    7  7 c c 3. ( f  g )  f   g  ( x 2  ln x)  2 x  4. ( f  g )  f   g  f  g  ( x 3  ln x)  3x 2  ln x  x 3  f 5.     g   c 6.     f   f   g  f  g g2 c f  f2 7.  f ( g ( x))  f ( g ( x))  g ( x)  x      ln x  2 1 x 2 x  ln x  x 2  1 x 1 x ln 2 x 2  5    5  3x  3   3 2  x  2 x 2  ln( x

3   5 x)    1  (3x 2  5) x  5x 3 2 1. Definíció szerint deriváljuk az f ( x)  x 2  5x  7 függvényt, az x0  2 helyen. Lássuk a definíciót! Az f (x) függvény differenciálható (röviden deriválható) az x0 pontban, ha értelmezve van az x0 pont egy környezetében továbbá létezik és véges a f ( x )  f ( x0 ) lim x x0 x  x0 Most az x0  2 helyen kell definíció szerint deriválni, tehát   f ( x)  f (2) x 2  5x  7  7 x 2  5 x  14 ( x  2)( x  7)  lim  lim  lim 9 x2 x2 x2 x2 x2 x2 x2 x2 így a függvény deriváltja az x  2 helyen 9. Jele: f (2)  9 lim 2. Definíció szerint számítsuk ki az f ( x)  x  2 x  3x  1 függvény deriváltját az 3 2 x0  1 helyen.   f ( x)  f (1) x3  2 x 2  3x  1  (1) x 3  2 x 2  3x  lim  lim  x 1 x 1 x 1 x 1 x 1 x 1 x( x 2  2

x  3) x( x  1)( x  3) 4  lim  lim x1 x1 x 1 x 1 lim 3. Differenciálható-e az f x   x 2  6 x függvény az x0  8 x1  5 x2  6 helyen? No ez már izgalmasabb, elsőként nézzük x0  8 helyen: x 2  6 x  16 f x   f 8 lim  lim  x8 x8 x 8 x 8 ha x  8 , akkor x 2  6 x  0 , vagyis pozitív, az abszolútérték tehát sajátmaga x 2  6x  x 2  6x x  8x  2  10 x 2  6 x  16  lim  lim x8 x8 x 8 x 8 Mivel létezik és véges ez a határérték, ezért differenciálható. Most jön az x1  5 x2  6x  5 f x   f 5 lim  lim  x5 x5 x 5 x 5 2 Mivel x  5 így x  6 x  0 tehát negatív, így az abszolútérték a mínuszegyszerese x 2  6x   x 2  6x x  5 x  1  4  x 2  6x  5  lim x5 x5 x 5 x 5 Végül x2  6 -ban nézzük  lim

Itt is differenciálható. 3 x 2  6x  0 x 2  6x f x   f 6 lim  lim  lim x6 x6 x6 x  6 x6 x6 Ha x  6 , akkor Amikor x 2  6 x milyen előjelű? x  6  0 , akkor x 2  6 x  0 , így x 2  6 x  x 2  6 x , Viszont ha x  6  0 , akkor x 2  6 x  0 , tehát x 2  6 x   x 2  6 x Itt tehát külön meg kell néznünk a jobb oldali és a bal oldali határértéket: x 2  6x lim x6 x60 x 2  6x lim x60 x6 x 2  6x x x  6   lim 6 x60 x  6 x60 x  6  lim  x2  6x  x x  6   lim  6 x60 x60 x6 x6  lim A jobb és a bal oldali határérték nem egyezik meg, tehát nem létezik a definícióban szereplő határérték tehát nem differenciálható. 4. Differenciálható-e az x  2 helyen, és ha igen, mi a deriválja a következő remek függvénynek? f x   x2  2x x 3

Alkalmazzuk a definíciót: x2  2x x 2  2x   8 8 f x   f 2   x 3 x 3  lim  lim  lim x2 x2 x2 x2 x2 x2 x  2x  12  14 x 2  2 x  8x  3 x 2  10 x  24  lim  lim x2 x  2x  3 x2 x  2x  3 x2 x  2x  3  lim A függvény tehát differenciálható, és f 2  14 5. Itt van a következő függvény:  x2 1 ha f x    2 2 x  x  1 ha Differenciálható-e az x2 x2 x  2 helyen? Ilyenkor először ellenőrizzük, hogy a függvény folytonos-e, majd azt, hogy a jobb oldali és a bal oldali derivált egyenlő-e. 4 1.lépés: folytonosság Az kell, hogy lim f ( x)  f (2) x2 f (2)  5 behelyettesítettük a 2-t a függvénybe (ahol meg van engedve az egyenlőség) Most jönnek a határértékek: Bal: lim f ( x)  lim 2 x 2  x  1  5

x20 x20 Jobb: lim f ( x)  lim x 2 1  5 x20 x20 Mivel a jobb és bal oldali határérték megegyezik, létezik határérték, és ráadásul ez egyenlő a függvényértékkel, így a függvény folytonos az x=2 helyen. 2. lépés: deriválás Bal oldali derivált: f   (2 x 2  x  1)  4 x  1 és f  (2)  8  1  7 Jobb oldali derivált: f   ( x 2 1)  2 x és f  (2)  4 Mivel a jobb és bal oldali derivált nem egyenlő, a függvény nem differenciálható az x=2 helyen. 6. Itt van a következő remek függvény: 3 x 2  6 x  8 ha  f ( x)   16 ha 2   x 4 x2 x2 Differenciálható-e az x  2 helyen? Ilyenkor először ellenőrizzük, hogy a függvény folytonos-e, majd azt, hogy a jobb oldali és a bal oldali derivált egyenlő-e. 1.lépés: folytonosság Az kell, hogy lim f ( x)  f (2) x2 f (2)  2 behelyettesítettük a 2-t a

függvénybe (ahol meg van engedve az egyenlőség) Most jönnek a határértékek: 5 Bal: lim f ( x)  lim x20 3 x20 x 2  6x  8  2 Jobb: 16 2 x 2  0 x  4 lim f ( x)  lim x 2  0 2 Mivel a jobb és bal oldali határérték megegyezik, létezik határérték, és ráadásul ez egyenlő a függvényértékkel, így a függvény folytonos az x=2 helyen. 2. lépés: deriválás Bal oldali derivált: f   (3 x 2  6 x  8 )    2x  6 1 2 x  6x  8 3 2 3 és f  (2)  10 12 Jobb oldali derivált:  16   32 x  és f  (2)  1 f    2   2 2  x 4 x 4   Mivel a jobb és bal oldali derivált nem egyenlő, a függvény nem differenciálható az x=2 helyen. 7. Itt van a következő remek függvény: 4 ln x  6 x  10  f ( x)   A 2  x 4  ha x 1 ha x 1 Milyen A szám esetén

differenciálható az x  1helyen? 1.lépés: folytonosság Az kell, hogy lim f ( x)  f (1) x1 f (1)  A behelyettesítettük az 1-et a függvénybe (oda, ahol meg van engedve az 5 egyenlőség) Most jönnek a határértékek: Bal: Jobb: A A lim f ( x)  lim 2  x10 x10 x  4 5 lim f ( x)  lim x10 x10 4 ln x  6 x  10  2 A jobb és bal oldali határérték akkor egyenlő, ha 6 A  2 tehát A  10 5 2. lépés: deriválás Bal oldali derivált:    A  0  x2  4  A  2x  f    2   2  x  4 x2  4 Jobb oldali derivált: f    4   és f  (1)   2A 25  3  1 7 1  ln x  6 x  10  ln x  6 x  10 4    6  és f  (1)  32 4 x  A jobb és bal oldali derivált akkor egyenlő, ha  2A 7  25 32 De mivel A=10 erre nem sok esély van így a függvény semmilyen A-ra nem

differenciálható az x=1 helyen. 7