Fizika | Felsőoktatás » Fizika képletek

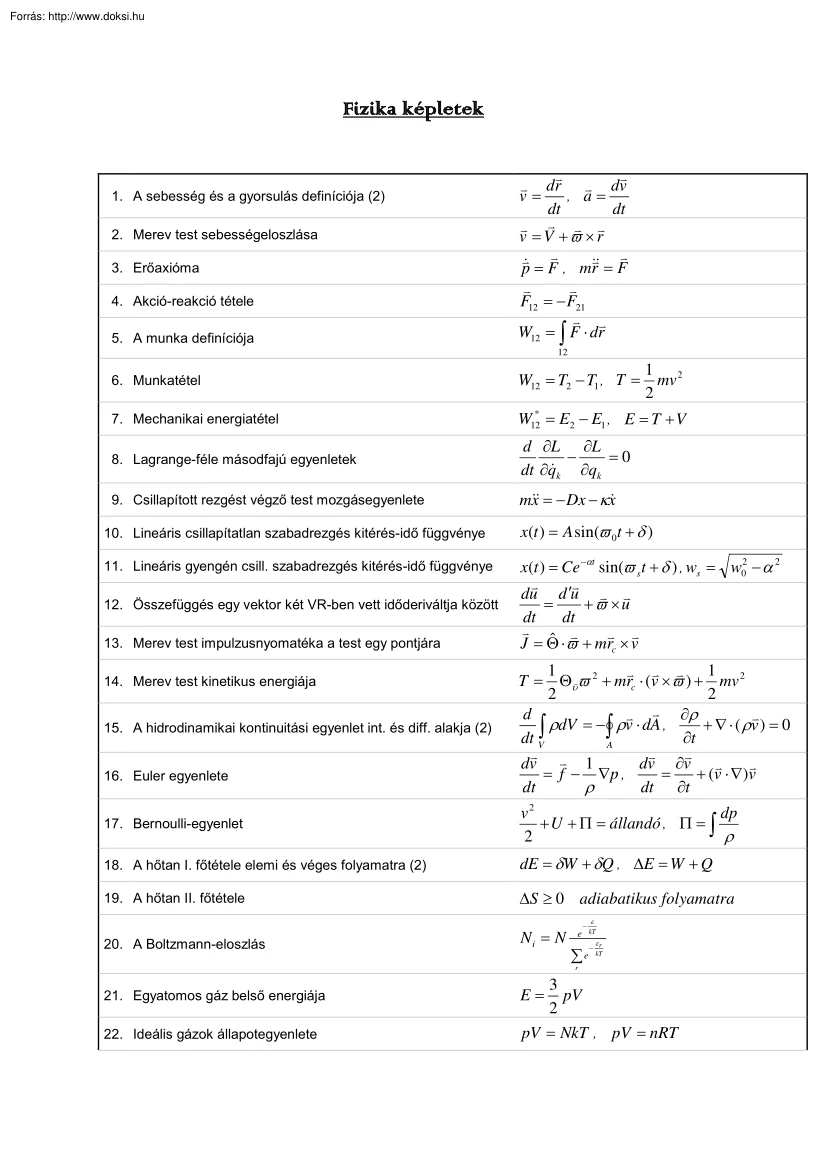
Fizika képletek 1. A sebesség és a gyorsulás definíciója (2) 2. Merev test sebességeloszlása 3. Erőaxióma 4. Akció-reakció tétele 5. A munka definíciója    dr  dv , a= v= dt dt     v = V +ϖ × r     p = F , mr = F   F12 = − F21   W12 = ∫ F ⋅ dr 12 1 2 mv 2 6. Munkatétel W12 = T2 − T1 , T = 7. Mechanikai energiatétel W12* = E2 − E1 , E = T + V 8. Lagrange-féle másodfajú egyenletek d ∂L ∂L − =0 dt ∂q k ∂qk 9. Csillapított rezgést végző test mozgásegyenlete mx = − Dx − κx 10. Lineáris csillapítatlan szabadrezgés kitérés-idő függvénye x(t ) = A sin(ϖ 0t + δ ) 11. Lineáris gyengén csill szabadrezgés kitérés-idő függvénye 13. Merev test impulzusnyomatéka a test egy pontjára x(t ) = Ce −αt sin(ϖ s t + δ ) , ws = w02 − α 2   du d ′u   = +ϖ × u dt dt  ˆ ⋅ϖ + mr × v J =Θ 14. Merev test kinetikus

energiája T= 12. Összefüggés egy vektor két VR-ben vett időderiváltja között 15. A hidrodinamikai kontinuitási egyenlet int és diff alakja (2) 16. Euler egyenlete c 1    1 Θυϖ 2 + mrc ⋅ (v ×ϖ ) + mv 2 2 2  d ∂ρ   ρdV = − ∫ ρv ⋅ dA , + ∇ ⋅ ( ρv ) = 0 ∫ dt V ∂t A     1 dv ∂v  dv  = f − ∇p , = + (v ⋅ ∇ )v dt ρ dt ∂t 17. Bernoulli-egyenlet v2 dp + U + Π = állandó , Π = ∫ 2 ρ 18. A hőtan I főtétele elemi és véges folyamatra (2) dE = δW + δQ , ∆E = W + Q 19. A hőtan II főtétele ∆S ≥ 0 adiabatikus folyamatra 20. A Boltzmann-eloszlás Ni = N − e ∑e ε kT ε − r kT r 21. Egyatomos gáz belső energiája 22. Ideális gázok állapotegyenlete 3 pV 2 pV = NkT , pV = nRT E= 23. Fundamentális egyenletek 24. A Clausius-egyenlőtlenség 25. Politrop gáz Poisson-egyenletei dE dV dH dp , dS = +p −V T T T T δQ dS ≥ Tk dS = pV κ = állandó , TV κ

−1 = állandó 28. A potenciálkülönbség számítása a térerősségből dp Q12 = dT T (V2 − V1 )  Qq  F = k 2 er r   U12 = ∫ E ⋅ ds 29. Az elektrosztatika I alaptörvénye, int és diff alak (2)     ∫ E ⋅ ds = 0 , ∇ × E = 0 26. Clausius–Clapeyron-egyenlet 27. A Coulomb-törvény 12 c 30. Az elektrosztatika Gauss törvénye, int és diff alak (2)    , D ⋅ d A = Q ∇ ⋅ D =ρ ∫ A 32. Elektromotoros erő   ∂ρ  d , ρ dV J d A = − ⋅ + ∇ ⋅ J =0 ∫A dt V∫ ∂t   U * = ∫ E ⋅ ds 33. Ohm-törvény teljes áramkörre U = I (R + r ) 34. Kirchhoff-törvények, csomóponti- és huroktörvény (2) ∑I 31. Töltésmegmaradás törvénye, int és diff alak (2) 12 35. Joule-törvény integrális alakja 36. Lorentz-erő képlete 37. Mágneses Gauss-törvény, int és diff alak (2) * i = 0 (csomópont ) , i ∑U i = 0 (hurok ) i P12 = U12 I    F = qv × B    , B ⋅

d A = 0 ∇ ⋅ B =0 ∫ A 38. Faraday-féle indukciótörvény, int és diff alak (2)     d   ∂B ∫c E ⋅ ds = − dt ∫A B ⋅ dA , ∇ × E = − ∂t 39. Soros RLC kör komplex és valós impedanciája (2) Z = R + i ϖL − ϖ1C , Z = R 2 + i ϖL − ϖ1C 40. Átlagteljesítmény soros váltóáramú körben P = U eff ⋅ I eff ⋅ cos ϕ 41. Effektív és csúcsérték kapcs szinuszos váltóáramú körben 42. Ampére–Maxwell-törvény, int és diff alak (2) 43. Poynting-vektor definíciója ( ) ) 2 I0 2      ∂D d   ∫c H ⋅ ds = I + dt ∫A D ⋅ dA , ∇ × H = J + ∂t    S = E×H I eff = 45. Monokromatikus síkhullám elektromos térerőssége 1 ∂ 2ψ ∇ 2ψ = 2 2 c ∂t    E = E0 cos(ϖt − k ⋅ r + δ ) 46. A Galilei-transzformációs egyenletek (x’, t’) x ′ = x − Vt , t ′ = t 44. Homogén hullámegyenlet ( 47. A Lorentz-transzformációs egyenletek (x’, t’) 1 V 

 x ′ = γ ( x − Vt ), t ′ = γ  t − 2 x , γ = 2 c   1 − V2 c 48. Relativisztikus tömegnövekedés 49. Relativisztikus mozgásegyenlet m = m0γ , γ = c ( ) 51. Relativisztikus kinetikus energia 52. Tömeg-energia ekvivalencia E = mc 2 53. A Planck-féle sugárzási törvény (spektrális eloszlás) U (υ , T ) = K 54. A Wien-féle eltolódási törvény 2 1 − V2     F = p = mv + m v d mc 2 dt T = m0c 2 (γ − 1) 50. Relativisztikus teljesítménytétel 1 P= T2 = υ 2 max hυ 3 hυ e kT − 1 T1 υ1 max ∞ 55. A Stefan–Boltzmann törvény E (T ) = σ ⋅ T , E (T ) = ∫ e(υ , T )dυ 4 0 56. Einstein-féle fotoelektromos egyenlet hυ = Wkilépési + Tmax 57. A foton impulzusa pf = 58. Radioaktív bomlástörvény és bomlásállandó (2) N (t ) = N 0 ⋅ e − λt , λ = 59. Bohr-féle frekvencia-feltétel ∆E = hυ 60. Bohr-féle kvantumfeltétel Le − = n ,  = 61. Energiaszintek a

H-atomban En = − E * ⋅ 62. A de Broglie-hullámhossz λ= 63. Határozatlansági reláció ∆x ⋅ ∆px ≥ h λ ln 2 T h , n = 1, 2, . 2π 1 n2 h p  2 * ∫ψ ψ dV = 1 64. Az 1-re normált hullámfüggvény teljes térre 65. Tartózkodási valószínűség w = ∫ψ *ψ dV 66. Hermitikus operátorok definíciója ( 67. A reguláris függvények skaláris szorzata (ψ 1 ,ψ 2 ) = ∫ψ 1*ψ 2dV 68. A sajátérték egyenlet  Hψ = k ⋅ψ 69. A Heisenberg-féle felcserélési törvények (2) [ p x , x ] =  , V ) (   Hψ 1 ,ψ 2 = ψ 1 , Hψ 2 ) teljes térre i [E ,−t ] = i 70. Az impulzus operátora a Schrödinger-reprezentációban 71. Az időfüggetlen Schrödinger-egyenlet 72. Az időfüggő Schrödinger-egyenlet 73. A középérték a kvantummechanikában  ∂   , px = x=x i ∂x 2  − ∇ 2ϕ + Vϕ = Eϕ 2m 2 2  ∂ψ − ∇ ψ + Vψ = − 2m i ∂t  x = (ψ , xψ ) 75. A szabad

részecskét leíró hullám egyenlete d 2x ∂V m 2 =− dt ∂x i  − ( Et − pr )  ψ (r , t ) = K ⋅ e  76. Az impulzusmomentum (L és L z ) sajátértékei (2) L =  ⋅ l ⋅ (l + 1), l 77. Kvantumszámok rendszere a H-atomban, fő~, mellék~ (2) En = − E * 78. K számok rendszere a H-atomban, mágneses~, spin~ (2) Lz = m, m = − l  0  + l , S z = ms , m s 79. Atommagok tömegdefektusa ∆m = M ( A, Z ) − Z ⋅ m p − ( A − Z ) ⋅ mn 74. Ehrenfest tétele = 0, 1  , Lz = m, m = − l  0  + l  1 , n = 1, 2,  , L =  ⋅ l ⋅ (l + 1), l = 0  n − 1 2 n = ± 1 2