Matematika | Analízis » A konvolúció alkalmazása és numerikus számítása

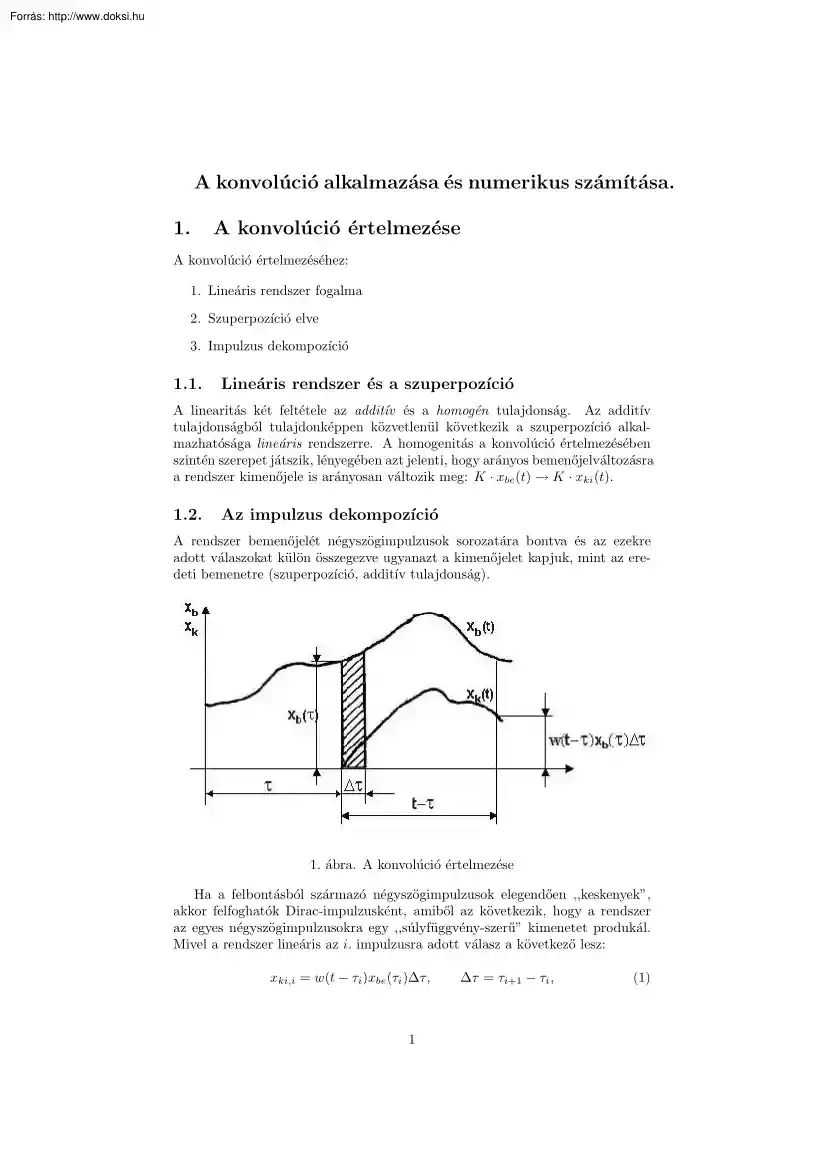
A konvolúció alkalmazása és numerikus számı́tása. 1. A konvolúció értelmezése A konvolúció értelmezéséhez: 1. Lineáris rendszer fogalma 2. Szuperpozı́ció elve 3. Impulzus dekompozı́ció 1.1 Lineáris rendszer és a szuperpozı́ció A linearitás két feltétele az additı́v és a homogén tulajdonság. Az additı́v tulajdonságból tulajdonképpen közvetlenül következik a szuperpozı́ció alkalmazhatósága lineáris rendszerre. A homogenitás a konvolúció értelmezésében szintén szerepet játszik, lényegében azt jelenti, hogy arányos bemenőjelváltozásra a rendszer kimenőjele is arányosan változik meg: K · xbe (t) K · xki (t). 1.2 Az impulzus dekompozı́ció A rendszer bemenőjelét négyszögimpulzusok sorozatára bontva és az ezekre adott válaszokat külön összegezve ugyanazt a kimenőjelet kapjuk, mint az eredeti bemenetre (szuperpozı́ció, additı́v

tulajdonság). 1. ábra A konvolúció értelmezése Ha a felbontásból származó négyszögimpulzusok elegendően ,,keskenyek”, akkor felfoghatók Dirac-impulzusként, amiből az következik, hogy a rendszer az egyes négyszögimpulzusokra egy ,,súlyfüggvény-szerű” kimenetet produkál. Mivel a rendszer lineáris az i. impulzusra adott válasz a következő lesz: xki,i = w(t − τi )xbe (τi )∆τ, 1 ∆τ = τi+1 − τi , (1) ahol a τi és ∆τ az (1) ábrának megfelelően értendő. Mivel a bemenet egy eltolt és skálázott Dirac-impulzus, a kimenet is egy eltolt és skálázott súlyfüggvény (homogenitás, kauzalitás, eltolás-invariancia). Ha egy impulzusra megvan a válasz akkor az additı́v tulajdonság miatt az egész bemenőjelre adott válasz xki (t) = N X w(t − τi )xbe (τi )∆τ , i=0 N= t , ∆τ (2) ahol N a felbontásban szereplő részintervallumok száma. Ha N -et

növeljük, akkor egyre pontosabb eredményt kapunk és limn∞ N mellett a (2) egyenlet a következőképpen alakul Z t xki (t) = w(t − τ )xbe (τ )dτ. (3) 0 A fenti (3) egyenletet konvolúciós integrálnak nevezzük. Meg kell jegyezni, hogy a fentiek során azzal a feltételezéssel éltünk, hogy a rendszer xbe bemenőjele és w súlyfüggvénye belépő jel, azaz xbe (t) ≡ 0, w(t) ≡ 0, ha t < 0. 2. A konvolúció alkalmazása A konvolúció fent definiált formája speciálisan arra használható, hogy egy rendszer súlyfüggvényének ismeretében tetszőleges bemenetre előállı́tható a rendszer válasza. Érdemes azonban tudni, hogy a konvolúció tágabb értelemben egy jóval általánosabb célú kommutatı́v1 matematikai művelet, melynek felhasználása nem korlátozódik a jelfeldolgozás területére. Tudni kell továbbá, hogy a a Laplace- és a Fourier-transzformációnak is vannak

konvolúció-tételei, ami azt jelenti, hogy az időtartománybeli konvolúció az operátortartományban (s vagy jω) szorzássá egyszerűsödik. 2.1 Diszkrét számı́tás Diszkrét függvények esetén a konvolúció a következő összefüggéssel adható meg xki [n] = n X w[n − i]xbe [i]. (4) i=0 3. Feladatok 3.1 RC-tag (folytonos) Határozzuk meg egy villamos RC-tag súlyfüggvényét, és ennek ismeretében adjuk meg a választ az alábbi bemenőjelekre! a, xbe (t) = ε(t) b, xbe (t) = Kε(t) 1 Ebben az értelemben a bemenőjel és a súlyfüggvény szerepe felcserélhető. 2 c, xbe (t) = δ(t) d, xbe (t) = e−αt Megoldás: Elsőként a rendszer súlyfüggvényét kell meghatároznunk, ami a rendszeregyenlet δ(t) bemenetre kapott megoldásaként adódik. A rendszeregyenlet dxki (t) + xki (t) = xbe (t). (5) dt A célszerűség kedvéért vezessük be a T = RC jelölést, és oldjuk meg az

egyenletet az x(t) = δ(t) esetre. A megoldásfüggvény a következő: RC 1 −t e T. (6) T Innen a (3) konvolúciós integrál alkalmazásával a kimenőjel már tetszőleges bemenetre megadható. R t t−τ t a, xki (t) = 0 e− T ε(τ )dτ = 1 − e− T xki (t) = t b, xbe (t) = K(1 − e− T ) (a homogenitás miatt) c, xbe (t) = w(t) (a definı́ció szerint) t 1 (e−αt − e− T ) d, xbe (t) = 1−αT 3.2 Egy példa a diszkrét esetre A bemenetek: xbe = [1, 2, 3, 4], w = [ 12 , 12 ]. A megoldás lépései: P0 xki [0] = i=0 w[0 − i]xbe [i] = w[0]xbe [0] = 21 P1 xki [1] = i=0 w[1 − i]xbe [i] = w[1]xbe [0] + w[0]xbe [1] = 12 + 1 = 32 . . 3