Physics | Mechanics, Quantum mechanics » Klasszikus mechanika

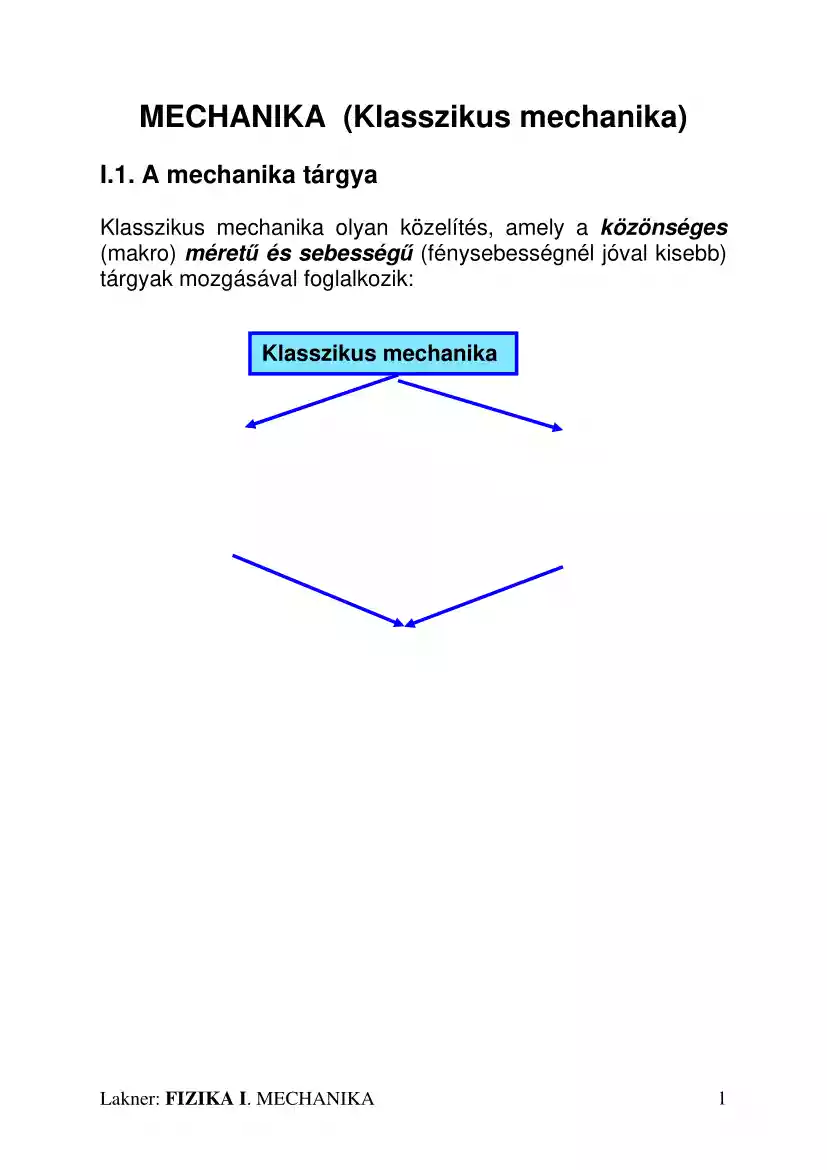
MECHANIKA (Klasszikus mechanika) I.1 A mechanika tárgya Klasszikus mechanika olyan közelítés, amely a közönséges (makro) méretű és sebességű (fénysebességnél jóval kisebb) tárgyak mozgásával foglalkozik: Klasszikus mechanika Mikroméretű (elemi részek) Kvantummechanika Fénysebességhez közeli Relativitáselmélet Relativisztikus kvantummechanika Lakner: FIZIKA I. MECHANIKA 1 I.2 Mértékrendszerek A mozgások térben és időben játszódnak le  Mennyiségek: Mennyiségek = mértékszám + mértékegység Kezdetben teljesen önkényes volt a megválasztásuk (font, láb, stb) Francia forradalom „természetes” mértékrendszer SI A mechanikában használt mértékegységek (Systeme Internatinal d Unite = SI)  Hosszúság: méter, m (Sevresi ősméter  a fény útja 1/299792458 s alatt),  Tömeg: kilogramm, kg (Sevresi platinahenger tömege),  Idő: Másodperc, s ( a 133 tömegszámú Ce atom megfelelő sugárzása 9192631770

periódusának időtartama),  Síkszög: Radián, rad (a kör sugarával megegyező körívhez tartozó szög),  Térszög: Szteradián, sr (a gömbsugár négyzetével egyenlő területhez tartozó középponti térszög). Ezek az alapmennyiségek, használatosak decimális törtrészeik (deci, centi, milli, mikró, nanó) és többszöröseik (., hektó, kiló), az időnél a perc, és az óra. Származtatott mennyiségek. Fizikai definició alapján Például: út m sebesség m 2 Sebesség   Gyorsulás   idő s idő s , m2  newton stb. Erő  tömeg x gyorsulás  kg x s Lakner: FIZIKA I. MECHANIKA 2 I.3 Az anyagi pont kinematikája Anyagi pont: kiterjedése nincs, tömege van,  közelítés Mozgás leírása: vonatkoztatási rendszer = koordinátarendszer y r y j k Derékszögű, jobbsodrású koordinátarendszer: P az anyagi pont, P r(t) a helyvektor az idő függvénye. x r(t) = x(t)i + y(t)j + z(t)k i z x, y, z a koordináták x z

i, j, k az egységvektorok Az r(t) helyvektor egy térgörbét ír le (vektorok vastagon jelölve, írásban képletben felülhúzva, r ). P r(t) s = út r = elmozdulás r(t+t ) P pálya A r a t alatt a P pontból a P pontba történő elmozdulás : vektor A s az ívhossz a t alatt megtett út: skalár A sebesség: időegység alatt megtett út: egyenesvonalú egyenletes mozgásra igaz. Általános esetbe a sebesség az r(t) helyvektor idő szerinti első deriváltja, azaz szintén vektor lesz: r dr  v  lim  r t dt gyakran jelölik ponttal is (időszerinti derivált). Koordinátákkal: Lakner: FIZIKA I. MECHANIKA 3    dx dy dz v i j k  x i  y j  z k  vx i  v y j  vz k dt dt dt v v v 2x  v 2y  v 2z a sebesség nagysága. Dimenziója: hosszúság/idő, mértékegysége: m/s A gyorsulás: időegység alatti sebességváltozás egyenletesen gyorsuló mozgásra igaz. Általában a

sebesség első (a helyvektor második) deriváltja: dv d 2 r a  2 dt dt  vagy  avr A gyorsulás derékszögű koordinátarendszerben:    a (t )  x (t )i  y j  z (t )k  ax i  a y j  az k a  a  a x2  a y2  a z2 . Dimenziója: sebesség/idő = hosszúság/időnégyzet, m/s2 . Legegyszerűbb eset: állandó gyorsulással rendelkező, egyenletesen változó mozgás. Legyen a gyorsulás a (gravitációs gyorsulás) továbbá t = 0 r = r0 és v = v0 kezdeti feltételek. A gyorsulás: dv a (t )  ebből d v  g d t . dt Kiintegrálva és a v(t=0) = v0 v (t )  a t  b a v(t=0) = v0 kezdeti feltétel miatt v (t )  a t  v 0 b = v0. A sebesség pedig a helyvektor deriváltja azaz v (t )  dr  at  v 0 . dt Lakner: FIZIKA I. MECHANIKA 4 Kiintegrálva a tömegpont helye mint az idő függvénye pedig: t2 r (t )  a  v 0t  r0 . 2 Eszerint a r = r(t) - r0 , azaz az elmozdulás

vektor mindig az a gyorsulás és a v0 kezdeti sebesség által meghatározott síkban van  síkmozgás: leírásához elegendő az x, y koordinátarendszer. Speciális esetek: 1. Szabadesés (Galileo Galilei, Pisai ferde torony) A gyorsulás: y h y(t) v g Lakner: FIZIKA I. MECHANIKA a = (0, -g, 0). A kezdeti feltételek: r0 = (0, h, 0) v0 = (0, 0, 0). g 2 y ( t )  h  t A mozgásegyenlet: 2 Az esési idő (y = 0): t m  2h g . A végsebesség: vm  gtm  2gh . 5 2. Ferde hajítás a = (0, -g, 0) r0 = (0, 0, 0) v0 = (v0cos, v0sin,0) y x(t) v0 y(t)  l h x : A koordináták mint az idő függvényei: A pálya egyenlete egy parabola: A repülési távolság (y = 0): v0 = kezdeti sebesség nagysága  = az x tengellyel bezárt szög x( t )  ( v0 cos )t g y( t )   t 2  ( v0 sin )t 2 g y( t )  2 2 x2  xtg 2v0 cos  2v cossin v0 l 0  sin2 g g Adott v0 kezdősebességnél akkor repül a

legmesszebbre, ha  = 450 2 v 0 sin  g v02 sin2  h 2g tm  A repülési idő (y = 0): A repülési magasság (h = y(tm/2): A valóságos pálya a levegő közegellenállása miatt az un. ballisztikus pálya y x Lakner: FIZIKA I. MECHANIKA 6 A mozgás leírása polárkoordinátákkal (síkmozgás) x(t)=r(t)cos(t) Pálya y(t)=r(t)sin(t) r(t) r(t)=r(t)(cos(t)i + sin(t)j )  A sebesség az r -nek a t szerinti első (szorzat), a gyorsulás a második deriváltja: Speciális esete a körmozgás: R    (t )   (t ) szögsebesség R = konstans er = cos(t)i + sin(t)j radiális egységvektor et = -sin(t)i + cos(t)j tangenciális egy.vektor Sebesség: v(t)=R(t)(-sin(t)i + cos(t)j)=R(t) (t) et tangenciális irányú Gyorsulás:  a(t)  R (cos( t )i  sin( t )j  R (  sin ( t )ι  cos( t )j ) 2  a(t)  R er  R et van radiális (befele mutató) és azaz

tangenciális komponense is. 2 Ha  = const. egyenletes körmozgás Ekkor a gyorsulásnak nincs tangenciális komponense, az a kör középpontja felé mutat: kerületi sebesség v = R 2 v 2 a a=R2 centripetális gyorsulás: acp  R R Lakner: FIZIKA I. MECHANIKA 7 I.2 Az anyagi pont kinetikája A kinetika feladata a mozgás közvetlen okainak ismeretében a mozgás meghatározása. (Ókori felfogás: a nyugalom a termé-szetes, a mozgás rendellenes)(Galileo Galilei, Isaac Newton) axiómák (Newton axiómák): 1. A tehetetlenség törvénye (Newton I axiómája): Minden test megtartja egyenes vonalú egyenletes mozgását vagy nyugalmi állapotát, mindaddig míg más testek ennek megváltoztatására nem kényszerítik  Tehetetlenség. Következménye: A mozgás a természetes, a nyugalom relatív, Inerciarendszer: olyan koordinátarendszer, ahol érvényes az I. axióma. (ha egy van akkor számtalan van: minden hozzá képest egyenes vonalú egyenletes

mozgást végző). Közelítés (pld. a Földhöz rögzített) 2. Az erő (kölcsönhatás) törvénye (Newton II axiómája): a mozgás megváltozása más testekkel való kölcsönhatás  mértéke az erő (F). A sebesség megváltozása arányos a testre ható erővel: dv 1  F dt m az arányossági tényező reciproka a tömeg, az m. Azt fejezi ki, hogy a test mennyire áll ellent az erőnek, mennyire akarja mozgását megtartani. Minél nagyobb annál inkább, így az m a mozgás megtartóképességének, a tehetetlenségnek a mértéke, így ezt a tömeget a test tehetetlen tömegének nevezzük. Az előzőek szerint:  d 2r m 2  mr  F dt Lakner: FIZIKA I. MECHANIKA 8 komponenseként egy-egy másodrendű differenciálegyenletet (összesen három) jelent,  m x  Fx   m y  Fy m z  Fz amik F(Fx,Fy,Fz) ismeretében, az említett kezdeti feltételek mellett (r(t=0)=r0(x0, y0, z0) és v(t=0)=v0(v0x, v0y, v0z)) megoldhatók. 3. Erő

ellenerő törvénye (Newton III axiómája): Minden erővel szemben fellép egy ugyanolyan nagyságú, de ellentétes irányú ellenerő. FAB A B FBA FAB = - FBA 4. Az erők szuperpozíciójának elve: Ha egy testre több erő hat, akkor ezek hatása helyettesíthető az eredőjük hatásával, azaz: F = F1 + F2 +.+ Fn ennek és a II. axióma felhasználásával:  mr  F   Fi a dinamika alapegyenlete. Az erő származtatott mennyiség, mértékegysége N (Newton) = kgm/s2. Az impulzus: a mozgásmennyiség p = mv jobban jellemzi a testet, mivel az erő hatására ez változok meg, Ennek megváltozása arányos az erővel (impulzustétel): dp d (m v )  F dt dt Lakner: FIZIKA I. MECHANIKA 9 a Newton II. törvényének általánosabb megfogalmazását jelenti, mivel a tömeg is változhat a mozgás közben (Forma-I versenyautó) A t1 t2 közötti impulzusváltozás (erőlökés) arányos lesz az erő integráljával: t2 p(t2 )  p(t1 )   Fdt t1

amely tartalmazza egyben az impulzus megmaradásának tételét is, ugyanis, ha egy testre ható erők eredője F = 0, akkor az előzőből p(t)= állandó. Az impulzust I-vel is jelöljük A munka A munka az erőnek az elmozdulás irányába eső vetületének és az elmozdulásnak (út) szorzata. Állandó erő és egyenes pálya esetén igaz. W = Fs  s IrI=s F r  W = IFI IrI cos W = F  r a két vektor skalárszorzata Fs s Amennyiben az erő nem állandó, akkor a pályát az A és B pont között felbontjuk n db ri elemi elmozdulásokra, amelyekhez tartozó Fi állandónak tekinthető, így az elemi munka: Wi = Fi ri . A teljes munka a pálya A és B pontja között az előzőek összege, azaz: n rB i 1 rA WAB   Fi ri   Fdr   ( Fx dx  Fy dy  Fz dz ) Lakner: FIZIKA I. MECHANIKA g 10 finomítva a felosztást átmegy integrálba (vonalmenti integrál). Értéke általában nemcsak az A és B végpontoktól

függ, hanem attól is, hogy milyen g görbe mentén végezzük az integrálást (vagyis az úttól is). Mivel dr=vdt ezért a munka az alábbi módon is felírható: W  rB tB rA tA  F d r   Fv dt . Származtatott mennyiség, egysége: J(Joule)=Nm= kgm2/s2. A mozgási energia Hogy egy test mozgásállapota hogyan változik, az nemcsak az erőktől, hanem azok munkájától is függ  munkavégzőképesség = energia. Az F=ma erő munkája az előzőek szerint: rB tB tB t B d 1 1 2 2 W   Fd r   m avdt    mv  dt   mv   dt  2  tA 2 rA tA tA ugyanis dvy d  1 2 1 d 2 2 2 1  dv dv   2vz z   va . vx  vy  vz   2vx x  2vy  v dt  2  2 dt 2 dt dt dt    Amennyiben a W = O, azaz nincs munkavégzés, akkor 1 2 mv  constans 2 a mozgó testre jellemző mennyiség, amit kinetikus (mozgási) energiának nevezünk. Amennyiben a test sebessége v1-ről (t1

időpillanatban) v2- re (t2 időpillanatban) változik, munkavégzés történik: Lakner: FIZIKA I. MECHANIKA 11 ha W0 azaz v2v1 a testen végeznek munkát ha W0 azaz v2  v1 a test végez munkát 1 2 1 2 mv2  mv1  W 2 2 A fenti összefüggést munkatételnek hívjuk. A nehézségi erő munkája Mozogjon egy m tömegpont a gravitációs térben, a = (0,-g,0). y F = (0, -mg, 0) r1 = (x1, y1, z1) r2 = (x2, y2, z2) r1 r mg r 2 y y2 z x A munka az előzőek alapján: r2 W   Fdr   ( Fx dx  Fy dy  Fz dz )  mg ( y1  y 2 ) r1 g látható, hogy az csak a magasságkülönbségtől függ és független attól, hogy milyen úton jutottunk az r1 pontból az r2-be. Az mgy mennyiséget az anyagi pont potenciális (helyzeti) energiájának nevezzük. A munkatétel értelmében ez a munka a mozgási energia megváltoztatására fordítódik, így a kettőt összevetve: 1 2 1 2 mv2  mv1  mgy1  mgy2 . 2 2 Lakner: FIZIKA I. MECHANIKA

12 Átrendezve egy fontos megmaradási tételt kapunk: 1 2 1 mv2  mgy 2  mv12  mgy1 azaz 2 2 1 2 mv  mgy  constans 2 a mechanikai energia megmaradásának a tétele. A megmaradási tétel nemcsak nehézségi erő esetén érvényes. Minden olyan esetben fennáll, amikor az erő munkája csak a két pont helyzetétől függ és nem függ az úttól (körintegrálja zérus). Az ilyen erőt konzervatív erőnek nevezzük (ilyenek még, többek között az elektromos és a mágneses erők). Ekkor érvényes a mechanikai energia megmaradásának tétele. Az F(r) erő egy vektor-vektor függvény, ezért a tér minden pontjához rendelhető egy-egy vektor, amelyek un. vektorteret alkotnak, amit erőtérnek nevezünk. Az E térerősséggel jellemezhető, ami az egységnyi tömegű (töltésű) pontra ható erő és így: F=mE Konzervatív erő(tér) esetén a térerősség előállítható egy (r) vektor skalár függvény teljes deriváltjaként, azaz (definíció

szerint annak negatív) gradienseként: E   grad  (r )  (    , , ) x y z azaz vektor lesz, amely a legnagyobb potenciálváltozás irányá-ba mutat. Az (r) függvényt az erőtér (skalár) potenciáljának hívjuk, akkor létezik, ha rotE=0 (egyenértékű a körintegrál zérussal). Lakner: FIZIKA I. MECHANIKA 13 Töltött részecskék mozgása elektromágneses mezőben Vákuumban viszonylag kis sebességgel (fénysebesség hatodánál kisebb, a relativisztikus effektus elhanyagolható) pontszerű részecskék mozgása, melyekre ható gravitációs erő szintén elhanyagolható. A q töltésre ható erő a Lorentz erő: F=qE+q(vxB) E a villamos térerősség, B a mágneses indukció, v a részecske sebessége. Speciális eseteket vizsgálunk: Elektromos térben történő mozgás. A mozgásegyenlet:  m r  qE kezdősebesség: v0 a) a kezdősebesség párhuzamos a térerősséggel: v0(v0,0,0), E(E,0,0) akkor a(a,0,0),

ahol a=qE/m egyenesvonalú, egyenletesen gyorsuló, (ha a kezdősebesség és az erő egyirányú) mozgás, illetve egyenletesen lassuló (ha ellentétes irányú). Az elektromos erőtér (gravitáció analógiájára) munkája: x2 W1, 2   qEdx  q( 2  1 )  qU ahol U = 1 - 2 potenciálkülönbség x1 Ha az elektron 1V potenciálkülönbségen átfut akkor 1eV=1,610-19J energiára tesz szert, amit az energiaegységként atomfizikában gyakran használunk. b) a kezdősebesség szöget zár be a térerősséggel, akkor a pálya a ferde hajításnál megismert y para-bolapálya lesz. Ha ez a szög 900-os, akkor: -q x qE 2 y x 2v 0 E az eltérítés arányos az E-vel, azaz az elektromos térerősséggel (potenciállal) Lakner: FIZIKA I. MECHANIKA 14 Katódsugárcsőben a felgyorsított elektronokat két egymásra merőleges lemezpár téríti el x és y irányba. A vizszintes eltérítőre un fűrészrezgést kapcsolnak, míg a függőlegesre a

vizsgált jelet. Mágneses térben történő mozgás A mágneses mező munkája: r2 t2 r1 t1 W1, 2   q( vxB)dr   q( vxB) vdt  0 azaz a mágneses tér nem változtatja meg a részeske sebességének a nagyságát, csak az irányát. Három eset: a) vIIB ekkor a részecskére ható erő 0, tehát a sebesség nem változik b) vB ebben az esetben a részecskére ható erő merőleges lesz annak sebességére (centripetális erő), azaz a részecske körmozgást végez, azaz: v2 qvB  m r v (q / m) B 2 q   B  körfrekvenciája T m az un. cikrotronfrekvencia ebből a pálya sugara: r  2 2   T A körülfordulási idő:  (q/ m)B független a részecske sebességétől és csak a q/m-től, a részecske fajlagos töltésétől függ. Lakner: FIZIKA I. MECHANIKA 15 c) A v szöget zár be B-vel. A sebességvektor v(v0cos, v0sin) A mozgás egy állandó menetemelkedésű csavarmozgás lesz, ahol a pálya sugara: r v0 sin

 (q / m) B körülfordulási idő pedig: T 2 (q/ m)B ezen idő alatt a részecske a függőleges irányban h távolságra jut, így a menetemelkedés: h  (v0 cos )T  2v0 cos (q / m)B Ezen az elven működik pl. a TV képcső eltérítője Lakner: FIZIKA I. MECHANIKA 16 Perdület (impulzusmomentum) Az m tömegű anyagi pontra ható F erőnek egy tetszőleges 0 pontra vonatkoztatott nyomatéka (momentuma) a forgatónyomaték (erő x erő karja): F  rsin r  M=Frsin amely vektor, azaz két vektor vektoriális (vektort eredményező szorzata: r x F = M. Hasonló módon értelmezhetjük az m anyagi pont impulzusának a nyomatékát is, perdületét, impulzusmomentumát: r x mv = r x p = L képezzük a perdület idő szerinti deriváltját: dL d d( m v ) dr  (r xm v )  xm v  r x dt dt dt dt az első tag 0 és a második pedig a forgatónyomaték, így dL M dt a végeredmény a perdülettétel (analóg az

impulzustétellel). Amennyiben M=0, akkor L=állandó vektor, a perdület megmaradásának a tétele (vö. az impulzus megmaradása tételével) Lakner: FIZIKA I. MECHANIKA 17 Kényszermozgás Az anyagi pont mozgását gyakran geometriai feltételek korlátozzák  kényszermozgás. Nézzük például a legegyszerűbb esetet a lejtőt 0 -N s G a súlyerő N a nyomóerő F N -N a nyomóerő ellenereje G F a testre ható erő  A testre ható erő: F = G + (-N) és F = G sin párhuzamos a lejtő síkjával. A mozgásegyenlet: gsin 2 t . 2 A matematikai inga : egy tömegpont leng egy felfüggesztett fonalon.  s m s  mgsin F = -mgsin Az erő  A mozgásegyenlet: ml    mgsin   l Kis kitérésekre: Megoldása: g F  G 2 ahol:   l g l    0 =0sin(t+) l T  2 g A lengési idő csak az inga hosszától függ, nem függ a kitérés nagyságától. Lakner: FIZIKA I.

MECHANIKA 18 Súrlódás A vízszintes lapra helyezett test csak egy bizonyos erő hatására mozdul el, a mozgó test lassul  súrlódás = súrlódó erő. A súrlódást az okozza, hogy a test hozzányomódik a felülethez, így nagysága arányos a nyomóerővel, azaz: S =  N. iránya párhuzamos a felülettel. A  a súrlódási együttható, függ a felülettől.  Tapadási súrlódás: meginduláskor  Csúszási súrlódás: kisebb a tapadásinál. Közegellenállás Közegben mozgó testre hat még egy erő, mivel a mozgó testnek "deformálni kell" a közeget. Ez az erő: K = - v  =q arányos a sebességgel, az arányossági tényező függ a közeg anyagi minőségétől () a mozgó tárgy keresztmetszetétől (q) és a  alaktényezőtől (amely síklapnál 1, gömbnél 0,6 és cseppnél 0.3) A mozgásegyenlet:  mr  F K   illetve m r +  r  F . Példa: a vízbe ejtett test sebessége

(ejtőernyős, stb.)  m v   v  mg K=-v  v  m v  g elsőrendű inhomogén differenciálegyenlet  s a homogén megoldása: F=mg v  ce  t m az inhomogén egy partikuláris megoldása: v=B így B=mg/ Lakner: FIZIKA I. MECHANIKA 19  A differenciálegyenlet a teljes megoldás: ahol a kezdeti feltételből, azaz: Így a vízbe ejtett test sebessége v  ce  t m c  mg  , mg    t mg  m v  1  e    a sebesség egy darabig nő, majd állandó marad. Lakner: FIZIKA I. MECHANIKA 20 1.3Tömegpontrendszerek és merev testek kinetikája Tömegpontrendszer: egymással kölcsönhatásban lévő tömegpontok összessége. n tömegpont, az i-edik mozgásegyenlete:  n mi r i  Fi   Fij , j 1 ahol az Fi a külső erő, míg az Fij a j-edik testről az i-edikre ható un. belső erő Összegezzük a mozgásegyenleteket az összes tömegpontra:  n m i

n n n n  F    F  F ri  i i 1 ij i 1 i 1 j 1 i i 1 a belső erők páronként kiesnek, mivel az erő ellenerő törvénye alapján Fij = -Fji . Vezessük be a n rS  mr i i i 1 n m n  mr i i n i 1 m i és a F   Fi i 1 i 1 a tömegközéppont (súlypont) koordinátáit és a pontrendszerre ható erők eredőjét. Ezek alapján a mozgásegyenlet:  m rS  F , azaz a pontrendszer tömegközéppontja úgy mozog mintha az erők eredője erre a pontra hatna. Ez a tömegközéppont tétele Az előzőekből:  d n mi r i  pi  F   dt i1 i 1 n azaz a rendszer összimpulzusának időszerinti deriváltja egyenlő a külső erők eredőjével. Ez az impulzustétel Ha F=0 az összimpulzus megmarad és a súlypont egyenesvonalú egyenletes mozgást végez, mialatt az egyes tömegpontok tetszőleges mozgást végezhetnek. Lakner: FIZIKA I. MECHANIKA 21 Ütközések

Centrális ütközés: A sebességek a két test súlypontját összekötő egyenesen fekszenek. A. Rugalmas ütközés Ebben az esetben mind az összimpulzus mind az összenergia megmarad: v1 v2 v2 v1 m2 m1 , , Az impulzusmegmaradás: m1 v1  m2 v 2  m1 v1  m2 v 2 1 2 1 2 1 1 , 2 , 2 mv  m v  m ( v )  m ( v ) 1 1 2 2 1 1 2 2 Az energiamegmaradás: 2 2 2 2 v1 és v2 -re két egyenlet, amiből azok meghatározhatók. Az ütközés mechanizmusa: a mozgási energiák a rugalmas alakváltozás következtében részben átalakulnak potenciálissá, majd vissza. B. Rugalmatlan ütközés csak az impulzus marad meg, az energia részben vagy egészében átalakul hőenergiává. v2 v m1 v1 m2 Az impulzusmegmaradás: m1v1 + m2v2 = (m1 +m2) v. Lakner: FIZIKA I. MECHANIKA 22 Ennek felhasználásával a kinetikus energia veszteség: 1 1 1 1 m1m2 E  ( m1v12  m2 v22 )  ( m1  m2 ) v 2  ( v1  v2 ) 2 . 2 2 2 2 m1  m2 Két esetet érdemes

vizsgálni: A: m2m1 és v2 =0 (egy autó betonfalnak ütközik). m v1 E  E1  1 m1v12 2 A teljes mozgási energiát elveszíti és így a roncsolódás a sebesség négyzetével lesz arányos. B: m1 = m2 és v1 = - v2 két azonos méretű és sebességű autó frontálisan ütközik: m1 m2 v1 v2  E  2  E 1  m1 v12 az egy autóra eső energiaveszteség akkora mint az A esetben. Lakner: FIZIKA I. MECHANIKA 23 1.4 A merev test kinetikája Helyzetét három pont, azaz kilenc koordináta határozza meg, amelyekből csak hat független, mivel a pontok kölcsönös helyzete nem változik  hat szabadsági fok (az energia kifejezésben független négyzetes tagok száma). Ez csökken, ha a mozgást korlátozzuk (egy pont rögzítésénél három, két pont esetén egy marad):  Haladó mozgás: a merev test minden pontjának sebessége azonos  pontrendszerek mozgása (súlyponttétel).  Forgó mozgás: a test minden pontja egy nyugalomban

lévő egyenes (tengely) körül körkörösen mozdul el. Szögsebességvektor és az elemi forgásvektor A P pont kerületi sebességének nagysága: v =   = r  sin   v P a szögsebesség vektorként értelmezve az v=xr  r igen kis dt időtartammal szorozva: vdt = dr = d x r O az elemi forgásvektor. A forgástengelyre vonatkoztatott impulzus- és tehetetlenségi nyomaték Tömegpontokra bontjuk a merev testet. Az i-edik tömegpont impulzusnyomatéka: Li = ri x m vi és vi =  x ri Legyen az y a forgástengely, ekkor  (0, ,0), tehát v i =  x ri = i j k 0  0 =  zí i -  xí k xí yí zí Lakner: FIZIKA I. MECHANIKA 24 és i j k xí yí z í mizi 0 mixi Li = ri x m vi = A teljes impulzusmomentumot megkapjuk, ha a fentit összegezzük minden i-re. Számunkra ennek csak a tengelyirányú (y) komponense a lényeges, mivel a kényszerfeltétel miatt a többi 0. Ez pedig: n n n L y   L iy    j( 

mi x  mi z )    mi ( xi2  yi2 ) . 2 i i 1 2 i i 1 i 1 Alkalmazva az alábbi jelöléseket: n  m (x i 2 i y ) 2 i i 1 n ml 2 i i i 1  , ahol a  mennyiség csak az i-edik tömegpontnak az y tengelytől mért li távolságától, azaz a test tömegének a forgástengelyhez viszonyított eloszlásától függ, amit a testnek a forgás-tengelyre vonatkozó tehetetlenségi nyomatékának nevezünk. Az impulzusmomentum ennek alapján: Ly =  hasonlít a p=mv kifejezéshez. Ez alapján a Newton II-nek megfelelő mozgásegyenlet tengely körül forgó testre: My  dL y dt   ω . Amennyiben a merev testre ható forgatónyomatékok eredője 0 az  szögsebesség állandó lesz (nemcsak nagysága, hanem iránya is  pörgettyű). A tehetetlenségi momentum számítása Ha a felosztást finomítjuk akkor a szumma átmegy integrálba, azaz    l 2 dm   l 2  dV , m V Lakner: FIZIKA I.

MECHANIKA 25 ahol a  a test sűrűsége mint a hely függvénye. Példaként nézzük egy homogén rúd súlypontján átmenő tengelyére számított tehetetlenségi nyomatékát. y dx A s  l 2 2  x Adx  A  x l 2 l3 12 mivel m =  l A a test tömege x z s  l 1 ml 2 12 A Steiner tétel: ha ismerjük a súlyponton átmenő forgás-tengelyre vonatkoztatott tehetetlenségi momentumot, akkor egy vele párhuzamos, a távolságra lévőre:  A   (x  a ) 2 dm   x 2 dm  2a  xdm  a 2  dm   s  ma 2 az első tag éppen a s, míg a második zérus (az integrálási intervallum szimmetrikus az origóra). a Steiner tétel azt is jelenti, hogy a súlyponton átmenő tengelyre vonatkoztatott tehetetlenségi momentum a legkisebb. Fizikai inga olyan merev test, amely vízszintes, nem a súlypontján átmenő tengely körül foroghat. A forgatónyomaték: My (0, M, 0) és M=-mgssin tengely A szögelfordulás:

 (0, , 0)   s súlypont A mozgásegyenlet: Megoldása:    0sin A lengésidő: mg Lakner: FIZIKA I. MECHANIKA mgs     2  t    T   T  2 m gs A lengésidő annál nagyobb, minél nagyobb a tehetetlenségi nyomaték és a tömeg hányadosa és minél közelebb van a súlypont a forgástengelyhez 26 Analógiák a mozgó tömegpont és a forgó merev test megfelelő összefüggései között: Tömegpont Helyvektor sebesség tömeg impulzus erő Merev test r v m p = mv F  Mozgásegyenlet mr  F energia E 1 2 mv 2 Lakner: FIZIKA I. MECHANIKA Elfordulás  Szögsebesség  Tehetetlenségi momentum  Impulzusmomentum L=  Forgatónyomaték M    M E 1 2  2 27 1.5 Rezgőmozgás Rugalmas erő hatására egy anyagi pont egyensúlyi helyzete körül rezgőmozgást végez. A rugalmas erő: F=-Dx, arányos az egyensúlyi helyzetből való kitéréssel,

ahol D a rugóállandó. x(t) Harmonikus rezgőmozgás Nincs csillapítóerő, így a mozgást leíró differenciálegyenlet (lineáris esetben és az x tengely mentén):  m x   Dx azaz  x   02 x  0 ahol 0  D m a körfrekvencia. A differenciálegyenlet megoldása: x(t )  A0 sin( 0t   0 ) az A0 a maximális kitérés, az amplitúdó, a  a fázisszög, amit sok esetben 0-nak veszünk). x A0 R  0 x(t)=Rsin -A0 Lakner: FIZIKA I. MECHANIKA Összevetve a harmonikus rezgőmozgást a körmozgással, látható, hogy az a körmozgásnak az x tengelyen vett vetülete. =0t+0 0 a t=0 időpillanatban a fázisszög. R=A0 az amplitúdó. 28 A harmonikus rezgőmozgás jellemzői: A frekvencia:   0 1 D  2 2 m 1 m   2  T A periódusidő: D   v  x   0 A0 cos(  0 t   0 ) A sebesség : akkor a legnagyobb, amikor a kitérés x(t)=0. Ebből a mozgási energia a t

időpillanatban (x(t) kitérés esetén): 1 1 EKIN  mv2  m02 A02 cos2 (0t  0 ) 2 2 A potenciális energia, azaz a –Dx erővel szemben 0 és x között végzett munka: x.  ( x ) 2  1 W   Dx dx  D   DA02 sin 2 ( 0t   0 )   2 0 2 0 x A teljes energia az előző kettőből (felhasználva a 02=D/m és a sin2+ cos2=1 összefüggéseket): E  EKIN  W  1 DA02  állandó 2 energia (mechanikai) megmaradás törvénye. Lakner: FIZIKA I. MECHANIKA 29 Csillapított rezgések Csillapítóerő: súrlódási erő (belső súrlódás), közegellenállás arányos a sebességgel, azaz  K   kv   k x ennek megfelelően a csillapított rezgőmozgás differenciálegyenlete:   x  2 x   02 x  0   ahol k 2m melynek megoldása: x(t )  A0e t cos(t   ) exponenciálisan csökkenő amplitúdójú, (A) rezgőmozgást eredményez, melynek frekvenciája:

   02   2 a sajátfrekvencia, kisebb mint a harmonikus rezgőmozgásé, de állandó. Kényszerrezgések A csillapított rezgőmozgásnál az amplitúdó és ennek megfelelően a rezgés energiája is folyamatosan csökken (a mechanikai energia átalakul hőenergiává). A rezgési állapot fenntartása érdekében ezt pótolni kell, mégpedig egy periódikus ( körfrekvenciájú) erő segítségével, amely: F  F 0 cos  t ennek felhasználásával a kényszerrezgés differenciálegyenlete az előzőek alapján:   x  2 x   x  a 0 cos t , ahol 2 0 a0  F0 m melynek megoldása: x (t )  A cos( t   ) Lakner: FIZIKA I. MECHANIKA 30 lesz, azaz a rezgőmozgás körfrekvenciája azonos lesz a kényszererőjével, -val, attól  fázisszöggel elmaradva. Az amplitúdó és a fázisszög pedig: A a0 ( 02   2 ) 2  4 2  2 , illetve tg    2  02   2 , azaz mindkettő

függ a kényszererő körfrekvenciájától és csillapodás mértékétől, miként azok az alábbi ábrákon láthatók: Lesz egy maximális amplitúdó, amelynek nagysága a csillapodás () növekedésével csökken és eltolódik az 0–nál kisebb frekvenciák felé, amelynek nagysága: AMAX  a0 2 és helye  0   02  2 2 , amit a rendszer rezonanciafrekvenciájának nevezünk és értéke valami2 2 vel kisebb, az   0   sajátfrekvenciánál. Amennyiben 0 a maximális amplitúdó kis  esetén az amplitúdó nagyon nagy lehet ( =0nál végtelen, rezonanciakatasztrófa). Lakner: FIZIKA I. MECHANIKA 31 Rezgések összegezése Ha több rezgés összeadódik, az eredő rezgés az egyes rezgések összege:  Két azonos frekvenciájú, azonos irányú és fázisú harmonikus rezgés összege egy olyan harmonikus rezgés, melynek fázisa és frekvenciája azonos az összeadandókkal, amplitúdója a két rezgés

amplitúdóinak összege (A=B+C).  Ha két rezgés frekvenciája és iránya azonos, de fázisai különbözők. A két rezgés eredője szintén harmonikus rezgés lesz: A sin(t   )  B sin(t   )  C sin(t   ) amelynek frekvenciája megegyezik az összegezendőkével, amplitúdója és fázisa pedig a két oldal összevetéséből: A2  B2  C2  2BCcos(  ) és tg   B sin   C sin  B cos   C cos  , azaz az amplitúdók vektorokként adódnak össze, melyek hossza az amplitúdók, irányszögei pedig a fázisszögek, miként az alábbi ábrán látható Lakner: FIZIKA I. MECHANIKA 32 Két egyszerű eset van: 1.     2n (n  0,1,2,3,) akkor A  B  C a két rezgés erősíti, 2.     (2n 1) (n  0,1,2,3,) akkor A  B  C a két rezgés gyen-gíti egymást. Amennyiben B=C ki is olthatják egymást Ha két rezgés irány és fázisa megegyezik, de frekvenciájuk

különbözik akkor az eredő rezgés többnyire periodikus, de nem harmonikus (lásd. a következő pontot) Lakner: FIZIKA I. MECHANIKA 33 Fourier analízis A Fourier analízis egy tetszőleges periódikus rezgés harmoni-kus rezgések összegeként állít elő:   n1 n1 x(t)  A0   An sinnt  Bn cosnt ahol A és B a Fourier együtthatók és n=1,2,3, A Fourier együtthatók a következők: A0  1  2  x(t)dt , 0 2 1 1 An  x ( t ) sin n  t dt B  n , 2 0 2 2  x(t ) cos ntdt . 0 Példa a négyszögrezgés Fourier sorba fejtése: Lakner: FIZIKA I. MECHANIKA 34 1.6 Hullámmozgás A rezgési állapot adott közegben tovaterjed, hullám keletkezik. A hullám időben és térben tovaterjedő rezgésállapot. A hullám fázisa a rezgési állapotát írja le. Az azonos fázisú pontok hullámfrontot, vagy hullámfelületet alkotnak (lehet sík-, kör-, gömbhullám). Két szomszédos, azonos

fázisú hely térbeli távolsága a hullámhossz (), időbeli a periódusidő (T) Hullámszám a 2 hosszúságú szakaszon elhelyezkedő hullámok száma, azaz: k  2  . A fázissebesség a fázis terjedési sebessége, azaz: v       T 2 ahol  a frekvencia. A hullámfüggvény (x irányba haladó harmonikus síkhullám): x u (t )  A0 sin  (t  )  A0 sin(  t  kx ) , v mivel az x helyen a fáziskésés (időkésés) -x/v. A hullámfüggvényt felírhatjuk komplex alakban is: x   u(t )  A0 exp i (t  )  A0 exp i(kx  t ) . v   Lakner: FIZIKA I. MECHANIKA 35 Tetszőleges k (vektor) irányba haladó síkhullám hullámfüggvénye, mint az r (helyvektor függvénye) pedig a következő lesz u (t )  A0 exp i (kr  t ) ahol a kr skalárszorzat. Nagyon sok esetben nem vagyunk kíváncsiak a hullámon belüli rezgésre így az „időtől független” hullámfüggvényre

az alábbi kifejezések is használatosak: u ( x )  A0 exp(ikx ) , illetve u ( x )  A0 exp(ikr) Interferencia Amennyiben két hullám találkozik egymással azok erősíthetik. Illetve gyengíthetik egymást (interferálnak) a frekvenciájuk és a közöttük lévő fáziskülönbség függvényében (lásd rezgések). Az alábbi speciális esetek a legfontosabbak : Két azonos hullámhoszszú, azonos terjedési irányú és n útkülönbségű síkhullámok interfereniája harmonikus hullámot eredményez, melynek amplitúdója a két hullám amplitúdójának összege (erősítik egymást). Két azonos hullámhoszszú, azonos terjedési irányú és 2n+1)/2 útkülönbségű síkhullámok interfereniájánál az amplitúdója a két hullám amplitúdójának különbsége (gyengítik egymást). Amennyiben a két amplitúdó egyenlő, kioltják egymást. Lakner: FIZIKA I. MECHANIKA 36 Hullámcsoport Hullámcsoport (hullámcsomag) akkor alakul ki, amikor azonos

amplitúdójú, különböző hullámhosszú és terjedésű irányú síkhullámok találkoznak. A maximum terjedési sebessége a csoportsebesség, vg különbözhet a fázissebességtől, v-től. A csoportsebesség: vg  v   dv d a fázissebesség hullámhosszfüggésétől (diszperzió, közegben való terjedés) függ. Amennyiben nincs diszperzió, a két sebesség megegyezik A térben korlátozott hullámcsoportot hullámcsomagnak nevezzük Állóhullámok Állóhullámok akkor alakulnak ki, amikor azonos frekvenciájú és amplitúdójú, de ellentétes irányú síkhullámok szuperponálódnak egymásra. Lakner: FIZIKA I. MECHANIKA 37 Két x irányú síkhullám esetén : x x x u(t )  A0 sin  (t  )  A0 sin  (t  )  2 A0 cos sin t v v v Az eredő hullám amplitúdója az x=/4, 3/4, 5/4 helyeken mindig nulla, ezek az állóhullámok csomópontjai, míg az x=/2, 3/2, 5/2 helyeken a maximumot éri el (duzzadóhelyek).

Longitudinális hullámoknál a rezgés iránya megegyezik a haladás irányával (levegő rezgései, hanghullámok), transzverzálisnál arra merőleges (elektromágneses hullámok, fény). Doppler effektus Ha egy nyugvó adó 0 hosszúságú (0 frekvenciájú), v sebességű (a nyugvó közeghez viszonyítva) hullámokat bocsát ki, akkor az ugyancsak nyugvó megfigyelő =0 és =0 frekvenciájú hullámokat vesz. Amennyiben a forrás v0 sebességgel mozog, akkor a vevő, ha az tőle mozog ’0, ha felé mozog ”0 hullámhosszat vesz, ugyanis: Mozogjon az adó a vevő felé. A T=1/0 rezgésidő alatt az adó v0T= v0/0, a hullám pedig 0 távolságot halad. A vevő által észlelt hullámhossz ennek megfelelően:   0  v0 0  v 0 (1  v0 ) v és a vevő által vett frekvencia: Lakner: FIZIKA I. MECHANIKA 38    0 /(1  v0 ) v azaz nagyobb (magasabb) lesz, mint az adóé. Az összefüggés csak

a v0v esetre érvényes, amikor a forrás sebessége átlépi a közegben lévő hullámsebességet, akkor egy hullámfal alakul ki (hangrobbanás) és a hullámokat maga után hagyja. Amennyiben az adó távolodik a vevőtől, hasonló meggondolások alapján:    0 /(1  v0 ) v pedig kisebb (mélyebb) lesz. A Doppler effektust alkalmazzák a radaros sebességmérésnél. De vele magyarázható az un vörös-eltolódás is, amennyiben egy csillag távolodik tőlünk, akkor színképvonalainak a nagyobb hullámhosszak felé (vörös szín felé) történő eltolódását észleljük, Laboratóriumban felvett színkép A csillagnál mért színkép Az eltolódás mértékéből megállapítható a csillagnak a Földhöz viszonyított sebessége, a világegyetem tágulásának a sebes-sége, amely: v   c, ahol a c a fénysebesség. Ha folyamatosan tágul, akkor volt egy időpont, amikor egy helyen (pontban volt), amely a tágulás sebességéből mintegy

15Mrd. évvel ezelőttinek adódott (Ősrobbanás). Lakner: FIZIKA I. MECHANIKA 39